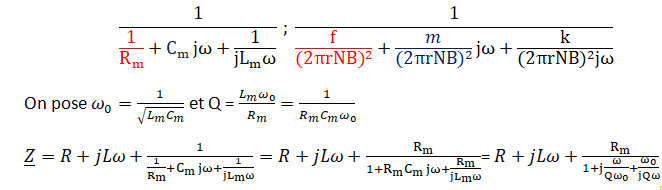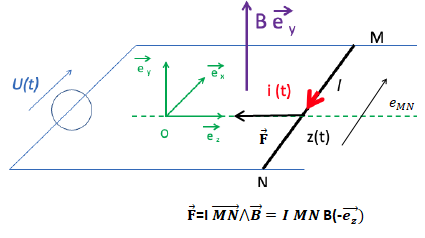
Le haut-parleur, concours interne ingénieur IEEAC et ICNA 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... I Préambule : Rails de LAPLACE Dans cette première partie, on travaille en coordonnées cartésiennes. Un courant d’intensité i(t) traverse une barre (MN), parallèle à l’axe (Ox), de longueur l. La barre est plongée dans un champ magnétique uniforme . Elle se déplace sans frottement à la vitesse v(t) sur deux rails parallèles à l’axe (Oz). Q1) Exprimer la force de Laplace F qui s’applique sur la portion de rail MN. Q2) Rappeler la loi de Lenz. Le courant induit dans le circuit tend à s'opposer par ses effets à la cause qui lui a donné naissance. Exprimer la force électromotrice induite eMN=VN-VM dans la portion de fil MN. Pendant la durée dt MN balaye une surface d'aire dS = MN v dt. Le flux coupé est dF = B MN v dt. La fem induite est e = -dF/dt = -B MN v. Cette fem a un sens tel que le courant induit  i s'oppose au déplacement de MN : Q3) Recopier le schéma en précisant la force de Laplace F pour i(t) >0 et la force électromotrice induite eMN pour dz/dt >0. II Modélisation du haut-parleur. Le haut-parleur électrodynamique est un système à symétrie cylindrique et on travaille dans la base indiquée sur la figure. 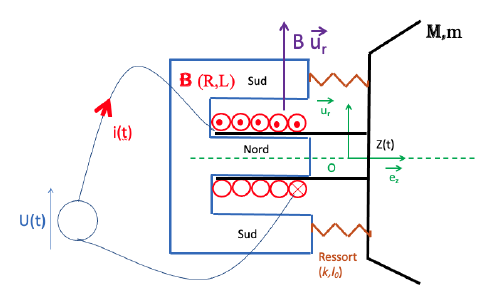L’aimant immobile d’axe (Oz) crée un champ magnétique B radial et uniforme dans l’entrefer. Une bobine B indéformable comportant N spires de rayon r est libre de se déplacer dans l’entrefer. Elle présente une résistance électrique R et une inductance propre L. La bobine est alimentée par une source de tension u(t). Une membrane M souple lui est attachée. Elle se déplace suivant l’axe z. 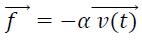Le mouvement de la membrane dans l’air engendre une force de frottement fluide L’ensemble B et M présente une masse m et est relié au bâti par un ressort de constante de raideur k et de longueur à vide l0. Au repos, la position de la membrane correspond à l’origine O. Q4) Exprimer la force de Laplace résultante sur la bobine  en fonction de N, r, B et i(t). F = i(t) 2pr N B dirigée vers la gauche. Par analogie avec les rails de Laplace, exprimer la force électromotrice induite eMN en fonction de N, r, B et dz(t) /dt. Le flux coupé est dF = B 2pr N v dt. La fem induite est e = -dF/dt = -B 2pr N v. Q5) Par application du principe fondamental de la dynamique appliqué à l’ensemble bobine-membrane, établir l’équation différentielle reliant z(t) et i(t) et leurs dérivées. La seconde loi de Newton s'écrit suivant ez : m z" = -kz -fz' - i(t) 2pr N B. Q6) Mettre l’équation sous la forme : d2z(t) /dt2 +adz(t) /dt +b z(t) = c i(t) (E1) Identifier a, b et c en fonction des paramètres de l’énoncé : m, k, a, N, r et B. z" +k/ m z +a / m z' = i(t) 2pr N B / m. a = a / m ; b = k / m ; c = 2pr N B / m. Q7) Par application d’une loi des mailles à l’ensemble générateur bobine, établir l’équation différentielle reliant u(t), i(t) et z(t) et leurs dérivées. u(t) -R i -Ldi/dt + e=0. Q8) Mettre l’équation sous la forme : u(t) = a' di(t) /dt +b' i(t) +c' dz(t) /dt (E2) Identifier a’, b’ et c’ en fonction des paramètres de l’énoncé : L, R, N, r et B. u(t) =R i +Ldi/dt +B 2pr N dz/dt.. a' = L ; b' = R ; c' = B 2pr N. III Schéma électrique équivalent. On se place en régime sinusoïdal forcé de pulsation w. On utilisera la notation complexe qui à une fonction sinusoïdale x(t)=X0 cos(wt+f) associe le complexe x(t)=X0exp(jwt) avec X0=X0 𝑒xp(jf). On prend la tension comme origine des phases u(t)=U0 cos(wt). Q9 à 12 Montrer, en combinant les équations (E1) et (E2), que l’ensemble bobine-générateur peut se représenter sous la forme d’un modèle électrique avec une impédance décrite par la figure suivante. 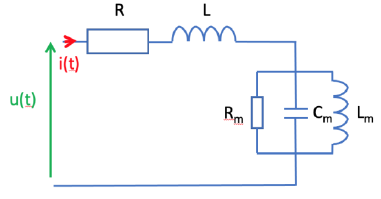admittance Ym =1/Rm +jCmw +1/(jLw). Z = R + jLw +1/ Ym =R + jLw +1/[1/Rm +Cmjw +1/(Ljw)]. d2z(t) /dt2 +adz(t) /dt +b z(t) = c i(t) (E1) u(t) = a' di(t) /dt +b' i(t) +c' dz(t) /dt (E2) Pour l'équation électrique : u - Ri -jLw i + j 2pr N w x B= 0. Pour l'équation mécanique :- m w2 x + k x + f j w x = - i 2pr N B. On élimine x par substitution : x = (- u + Ri +jLw i ) / ( j 2pr N w B). Repport dans l'équation mécanique : (-m w2  + k + f j w )(- u + Ri +jLw i ) / ( j 2pr N w B)= -  i 2pr N B. Regrouper les termes : u . (m w2  - k - f j w ) = i [ (m w2  - k - f j w )( R + j Lw) - jwB2 (2pr N)2 ]. Z = - jwB2 (2pr N)2  / (m w2  - k - f j w ) +  R + j Lw. Z = wB2 (2pr N)2  / (jm w2  -j k + f  w ) +  R + j Lw. Z = B2 (2pr N)2  / (jm w  -j k /w + f  ) +  R + j Lw. Z = B2 (2pr N)2  / (m jw  + k / (jw) + f  ) +  R + j Lw. ... .... Q13) Proposer un protocole expérimental (avec schéma, appareil de mesures et principe d’exploitation) permettant de déterminer l'impédance du haut-parleur. Mettre en série GBF, haut-parleur er une résistance de quelques dizaines d'ohms. Oscilloscope branché aux bornes de la résistance et du haut-parleur. Q14) Quelle est la bande passante d'un oscilloscope ? Quelle est celle d'un multimètre ? Bande passante oscilloscope : de 60 MHz à 200 MHz. Bande passante d'un multimètre numérique robuste : 40 Hz à 30 kHz. Q15) En utilisant la courbe expérimentale  donnant le module de l’impédance Z en fonction de la fréquence en échelle log-log, déterminer, en expliquant votre démarche, les valeurs de R, L et w0. Si w est faible, Z tend vers R spoit environ 12 ohms. Pour w = w0   la courbe présente un maximum. w0 = 2 p f0 ~2 x3,14 x45 ~280 rad /s. Si w est grand Z tend vers R+jLw. |Z|=[R2+(Lw)2]½. Pour f = 20 000 Hz, w =2 x3,14 x20 000 ~1,3 105 rad /s ;  |Z|~ 80. R2+(Lw)2=802=6 400. Lw ~80 ;  L ~ 6 10-4 H. Q16) Pour déterminer les valeurs de k et m, on va faire varier la masse de la membrane en ajoutant sur la membrane une petite masse m’. Quelle est alors la nouvelle pulsation de résonance ? w'0 = (k /(m+m')]½ ;  w0 = (k / m]½. Quelle courbe tracer pour obtenir une droite expérimentale permettant de déterminer séparément k et m ? On expliquera clairement la démarche. Supposons que m = 15 g, estimer les valeurs de k et de la compliance de suspension C = 1 / k. log(w'0 ) = 0,5 log(k) -0,5 log(m+m'). Mettre en abscisse  : log(m+m') et en ordonnée : log(w'0 ). L'ordonnée à l'origine permet de trouver k. Connaissant k, w0 = (k / m)½permet de trouver m. w0 = (k / m)½ =280 ; k / m =7,8 104 ; k = 7,8 104 x0,015 =1,2 103 N / m ; C =8,5 10-4 m /N.

menu