Physique chimie, concours Geipi Polytech  2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1. Partie A : L’hydrogénocarbonate de sodium, connu aussi sous l’appellation bicarbonate de soude, est un composé minéral de formule NaHCO3 aux multiples usages. Soluble dans l’eau, il se décompose en deux espèces ioniques : l’ion sodium Na+ et l’ion hydrogénocarbonate HCO3- .  I-1- Donner le schéma de Lewis de l’ion hydrogénocarbonate. 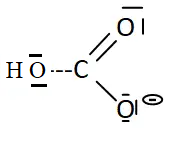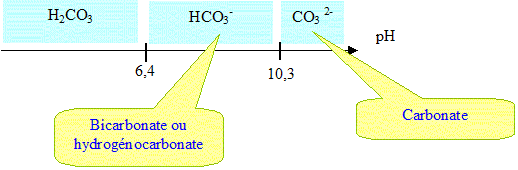L’ion hydrogénocarbonate est impliqué dans deux couples acidobasiques : HCO3- / CO32- de pKa1 = 10,3 et H2CO3 / HCO3- de pKa2 = 6,4 I-2- Quel terme permet de qualifier une telle espèce qui peut jouer le rôle d’un acide ou d’une base ? Amphotère.  I-3- Indiquer les espèces chimiques dominantes en fonction du pH (diagramme de prédominance).  Partie B : On dispose d’une solution aqueuse d’hydrogénocarbonate de sodium commerciale dont on veut vérifier la concentration. On se propose de doser un échantillon de volume V1 = 50,0 mL par une solution d’acide chlorhydrique (monoacide fort) de concentration 2,0⨯10-1 mol.L-1 selon la réaction : HCO3- + H3O+ --> H2CO3 + H2O.  On suit la valeur du pH en fonction du volume de la solution d’acide ajouté comme le montre la courbe de dosage ci-dessous. I-4- Calculer le pH de la solution titrante d’acide chlorhydrique. pH = -log (c) = -log (0,20) ~0,7.  I-5- La concentration massique indiquée sur le flacon commercial de la solution d’hydrogénocarbonate de sodium à titrer est : 16 g.L-1, déterminer la concentration molaire correspondante. 16 / M(NaHCO3) = 16 / 84=0,19 mol / L.  I-6- D’après la courbe de dosage pH = f(VHCl aq), mesurer le volume équivalent puis en déduire concentration réelle de la solution d’hydrogénocarbonate de sodium. 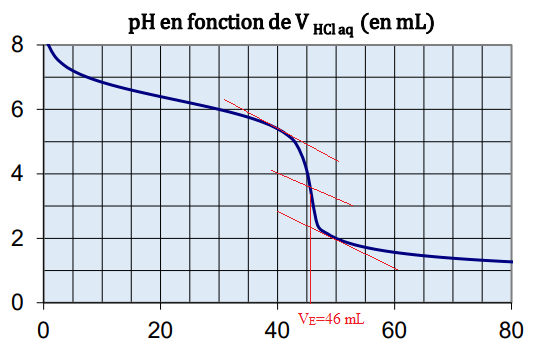C V1 = [HCl] VE ; C =0,20 x46 / 50 ~0,18 mol / L. Partie C : L’hydrogénocarbonate de sodium se décompose sous l’effet de la chaleur pour donner du carbonate de sodium, du dioxyde de carbone (gaz) et de l’eau (gaz) selon l’équation-bilan : 2 NaHCO3 solide --> Na2CO3 solide + CO2 gaz + H2O gaz.  On chauffe un échantillon de 0,050 mol d’hydrogénocarbonate de sodium jusqu’à obtenir une masse constante de solide blanc.  I-7- Déterminer le volume de gaz dégagé lors de l’expérience. n(CO2) + n(H2O) = n = 0,050 mol. Volume molaire des gaz : 24 L/mol. V = 0,050 x24 =1,2 L.  I-8- Déterminer la masse finale de produit solide à l’issue du traitement thermique n(Na2CO3) =0,5 n = 0,025 mol. M(Na2CO3) =106 g /mol. m = 0,025 x106=2,65 g. Exercice 2. L’électrification du parc automobile mondial à l’horizon 2050 devrait entraîner une multiplication par 4 de la demande de nickel entrant dans la fabrication des batteries. 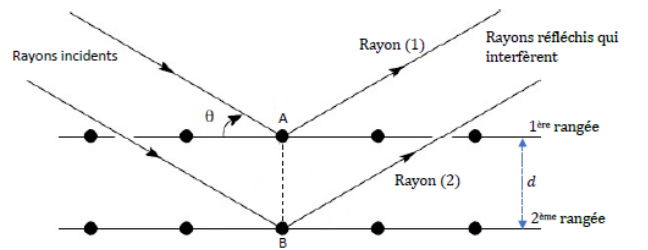On se propose ici d’analyser un cristal de nickel en déterminant la distance entre les plans d’atomes. Pour simplifier, on considère deux rangées d’atomes séparées par du vide et éloignées l’une de l’autre d’une distance d (voir figure ). Lorsqu’on envoie une onde de longueur d’onde l = 0,154 nm sur le cristal, les rayons réfléchis par les atomes interfèrent. Ici, on ne considère que les ondes qui vont interférer avec l’atome situé au point A d’une première rangée et l’atome situé au point B d’une deuxième rangée (voir figure). Les rayons incidents sont parallèles entre eux et forment un angle q avec les rangées d’atomes. Après avoir été réfléchis par les atomes, ils repartent parallèles entre eux et forment à nouveau le même angle q avec les rangées. Les ondes réfléchies vont alors interférer entre elles pour une valeur particulière de cet angle q. II-1- Afin que les interférences soient constructives, comment doivent vibrer les ondes correspondant aux rayons (1) et (2) ? Les ondes doivent être en phase ou décalées d'un nombre entier de longueur d'onde..  II-2- Afin d’illustrer la question précédente, choisir la situation correspondant à des interférences constructives. 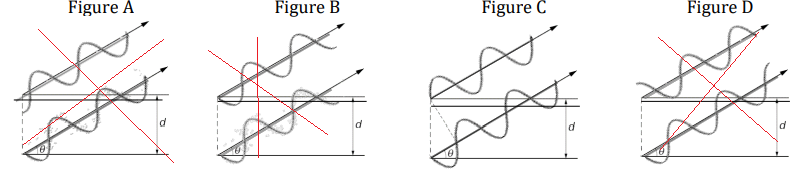II-3- Donner l’expression de la différence de chemin optique d à partir des longueurs des segments pertinents entre les points de la figure 2 ci-dessous. 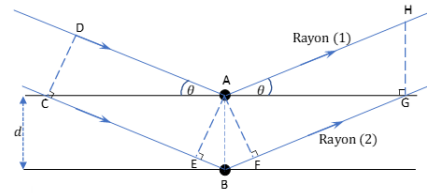II-4- Cocher la réponse donnant l’expression de la différence de chemin optique d = 2 EB =2 d sin q.  II-5- Quelle relation doit-il y avoir entre le chemin optique et la longueur d’onde pour que les interférences soient constructives ? d = k l avec k entier naturel. II-6- On obtient des interférences constructives pour un angle q = 25,9°. Dans le cas où la valeur de d est la plus petite, calculer la valeur de d . 2 d sin q = l  ; d = l / (2 sinq) =0,154 10-9 /(2 sin25,9)=1,76 10-10 m.  II-7- Le tableau ci-dessous représente le spectre en fréquence des ondes électromagnétiques. Montrer que l’onde utilisée appartient au domaine spectral des rayons X. f = c / l = 3,0 108 / (0,154 10-9) =1,9 1018 Hz. ... .... Exercice III. Lors de la mise au point de nouveaux pneumatiques, des tests d’adhérence sur circuit sont effectués. On étudie alors la force exercée par le sol sur le véhicule, qui est directement liée au contact des pneus sur la piste. Un véhicule d’essai de masse m = 700 kg repéré par le point M se déplace sur la portion de circuit horizontale représentée sur la figure. La trajectoire du véhicule y est représentée en pointillés. On donne  l’évolution au cours du temps de sa vitesse v(t) entre les points M1 et M4. L'axe vertical est ascendant. Mouvement dans la ligne droite entre M1 et M2 :  III-1- Donner les coordonnées du vecteur vitesse v du véhicule entre M1 et M2. Le temps t est exprimé en secondes, et les vitesses en mètres par seconde. On donne les constantes A, B et C dans les unités du système international : A = 4,90 ; B = 3,00 ; C = 35,0. vx = 0 ; vy = -Bt+C ; vz =0 . III-2- A partir de vos réponses à la question 1, déduire les expressions des coordonnées du vecteur accélération⃗ du véhicule, entre les points M1 et M2. ax=0 ; az=0 ; ay =-B.  En plus de son poids P, le véhicule subit la réaction du sol, qui se décompose en deux forces R⃗ (la réaction normale  est perpendiculaire au sol) et la réaction tangentielle f, tangente au sol, est due aux frottements des pneus sur la piste. Les frottements du véhicule avec l’air sont négligés.  III-3- A l’aide de la relation fondamentale de la dynamique appliquée au véhicule dans le référentiel terrestre, donner la relation entre R, f , P, a et m. III-4- Le mouvement du véhicule d’essai s’effectue dans un plan horizontal. Compléter le schéma en représentant les forces appliquées au véhicule au point M2. III-5- En déduire les expressions littérales puis les valeurs des forces au point M2. Suivant l'axe vertical : P = mg = R = 700 x 9,8 =6860 N Suivant l'axe horizontal : -f = m ax=m B. f = 700 x3,00 = 2100 N. Mouvement dans la courbe : étude dans le repère de Frenet  A partir du point M3, le pilote d’essai maintient une vitesse constante v3 = 10,0 m/s et suit jusqu’au point M4 une trajectoire de rayon constant r = 16,0 m. Dans toute la suite, on ne considère plus les forces N et P : tout se passe comme si le véhicule n’est soumis qu’à la force  f au cours de son mouvement.  III-6- Comment appelle-t-on le mouvement de la voiture entre M3 et M4 ? Mouvement circulaire uniforme.  III-7- Déduire les caractéristiques de la réaction tangentielle f subie par le véhicule d’essai au cours de son mouvement entre les points M3 et M4. f est dirigée vers le centre du cercle. f = m v23 / r  Pour les pneus testés, la force f dûe aux frottements avec la piste, ne peut pas dépasser la valeur de 9200 N. Si le mouvement du véhicule nécessite une valeur de f supérieure, alors le véhicule dérape. Pour un rayon r = 16,0 m, f vaut 4,38.103 N. III-8- Quelles autres trajectoires de rayon constant le pilote pourrait-il suivre à vitesse v3 constante dans la courbe sans risquer de déraper ? f r =m v23 = constante =4,38 103 x16 =7,008 104. f < 9200 ; r > 7,008 104 / 9200 ; r >7,6 m Trajectoires possibles : toutes les trajectoires de rayons supérieurs à 16,0 m et toutes les trajectoires de rayons supérieurs à 8,0 m.

menu