Dans un
canon de microscope électronique, un électron 𝐴 (masse m
, charge électrique −e) est émis, avec une vitesse initiale
négligeable, le long d’un axe Ox, par une plaque métallique P
1
portée à un potentiel nul. Cet électron est accéléré, dans le vide,
grâce à une grille métallique P
2 portée à un potentiel
constant Va = 100 V . Les plaques P
1 et P
2 sont
habituellement
appelées cathode et anode, respectivement

1. Quelle est la vitesse v de A lorsqu’il atteint l’anode ?
Le poids de l'électron est négligeable devant la force électrique.
Travail de cette force W = e Va.
Théorème de l'énergie cinétique entre P
1 et P
2.
½m v
2-0 = e Va ; v = (2 e Va / m)
½.
Réponse B.
2. Calculer v. On indique les valeurs approximatives des constantes fondamentales suivantes : m~ 9 × 10
−31 kg et la charge
élémentaire e ~ 1,6.10
−19 C
.
v =(2 x1,6 10-19 x100 / (9 10-31))½ ~6 106 m /s Réponse C.
3. Quelle est la longueur d’onde de De Broglie,
l d’un électron de vitesse v ? h ~ 6,63 × 10
−34 J. s désigne la constante de
Planck
l = h / p = h / (mv)= h / (
2 e Va / m)½.
Réponse A.
l=6,63 10
-34 /(9 10
-31 x6 10
6)=1,2 10
-10 m ~ 100 10
-12 m=100 pm.
Réponse C.
4. Une fois la vitesse v acquise, on s’arrange à la sortie (non représentée sur la figure) du canon pour que l’électron pénètre
dans une région où règne seulement un champ magnétique B , stationnaire et uniforme, dont la direction est perpendiculaire
à la direction de la vitesse incidente de l’électron. Que dire quant à la trajectoire de l’électron dans cette région ?
A) L’électron n’est pas dévié et suit donc une trajectoire rectiligne.
B) La trajectoire de l’électron est une parabole.
C) La trajectoire de l’électron est circulaire de rayon proportionnel à B.
D) La trajectoire de l’électron est circulaire de rayon proportionnel à Va
½ / B
.
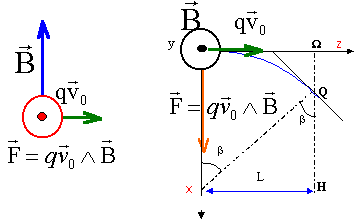
Le mouvement s'effectue dans le plan défini par la
vitesse et la force magnétique.
Cette force est centripète ; dans la base de
Frenet (suivant l'axe n) la 2ème loi de
newton s'écrit :
qv0B = mv20 / R soit R =
mv0 / (qB) = Cte.
la trajectoire est un arc de cercle.
v=v0 = (2 e Va / m)½ ; q = e.
R=(2 e Va m)½ / (eB). Réponse D.
5. Lorsque l’électron quitte la région où règne le champ magnétique, que peut-on dire de son vecteur vitesse v et de sa
trajectoire (on négligera l’influence du poids).
La force de Lorentz perpendiculaire à la vitesse, ne travaille pas. Le poids est négligé.
L'énergie cinétique, et donc la norme de la vitesse, de l'électron restent constantes. Réponse A.
A la sortie du champ magnétique, aucune force n'agit sur l'électron ;
d'après la première loi de Newton, l'électron est animé d'un mouvement
rectiligne uniforme. Réponse D.
6. On s’intéresse à l’angle
q, dit de déflexion magnétique, que forme la direction du vecteur vitesse v avec l’axe Ox lorsque A sort de la région
du champ magnétique. Cet angle est
q = [e /(2mVa)]
½BL
a,
où
a est un nombre réel et L une longueur ; précisément, L est la longueur de la trajectoire de l’électron dans la région du
champ magnétique. À l’aide d’une analyse dimensionnel, déterminer
a.
On pose w =eB / m, pulsation cyclotron ( rad / s).

w L a la dimension d'une vitesse ; wL / v est sans dimension.
Un angle est sans dimension. Donc a = 1.
q = e m / v BLa.
Réponse C.


