Mouvement de la valve d'une roue de vélo, glissade sur un hémisphère, concours ENAC 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... On s’intéresse à la trajectoire et aux grandeurs cinématiques (vitesse, accélération) de la valve d’une roue (centre 𝐶, rayon 𝑅) de vélo dans le référentiel du laboratoire R. Cette valve est assimilée à un point M. Le mouvement de M est analysé dans R ; on suppose qu’il s’effectue dans le plan Oxy, où O est l’origine du repère cartésien ; x et y désignent respectivement les coordonnées cartésiennes de M. 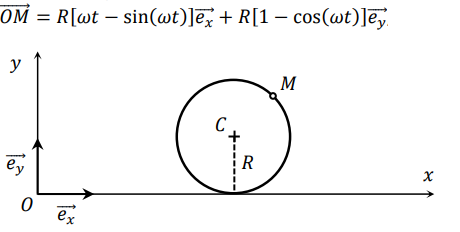w est une grandeur constante. 1.  Quelle est l’expression du vecteur vitesse v de M dans R ? 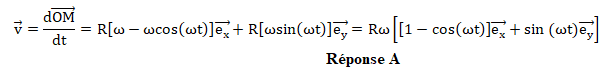 2. Déduire la norme du vecteur vitesse. v = Rw [(1-cos(wt))2 +sin2(wt)]½. v = Rw [2(1-cos(wt))]½ = 2½Rw [1-cos(wt)]½ . Réponse B.  3. Quelle est l'expression du vecteur accélération dans R ? Dériver l'expression du vecteur vitesse par rapport au temps. 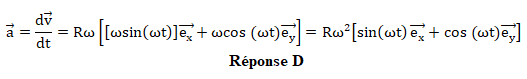  4. Parmi les propositions suivantes, lesquelles sont exactes ?  A) La vitesse de M ne s’annule jamais.  B) L’accélération de M ne s’annule jamais. Vrai.  C) Les composantes ay et vx s’annulent aux mêmes instants.  D) La vitesse de M s’annule aux instants t = 2 p n / w où n est un entier naturel. Vrai. La norme du vecteur vitesse s'annule si cos (wt) = 1. wt = 2pn ; t = 2 p n / w où n est un entier naturel. La composante ax de l'accélération de M s'annule si sin (wt) = 0 ; t =  2 p n / w où n est un entier naturel. La composante ay de l''accélération de M s'annule si cos (wt) = 0 ; t =  (2n+1) p  /(2 w) où n est un entier naturel. Les deux composantes de l'accélération ne peuvent pas s'annuler simultanément. La composante vx de l'a vitesse de M s'annule si cos (wt) = 0 ; t =  2 p n / w où n est un entier naturel.   5. Quelle est la distance parcourue par le centre C de la roue lorsque t = 2 p  / w ? 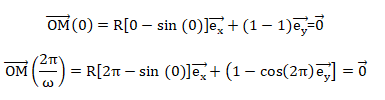A l'instant initial, la valve est en O, c'est à dire à la verticale du point C. A t = 2p/w, la valve se retouve à la verticale de C. Selon l'axe Ox, les points C et M ont avancé de la même distance 2pR. Réponse B.   6. On appelle rayon de courbure, r(𝑡), à la trajectoire en un point M à l’instant t, le rayon d’un cercle tangent particulier appelé cercle osculateur. Ce cercle unique " épouse au mieux la courbe en M" . 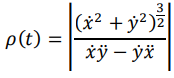On admet que l’expression du rayon de courbure est, ici : Donner l’expression de r(t) pour le mouvement de M. 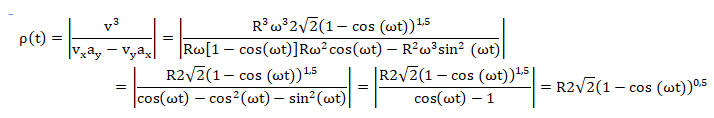Réponse D. ... .... Un corpuscule matériel A (masse m) glisse, sans frottement, sous l’action de son poids sur la surface d’un hémisphère de rayon r. On suppose que le mouvement de A s’effectue dans un plan vertical. Le référentiel terrestre, lié à l’hémisphère dans lequel on étudie le mouvement de A est supposé galiléen. Ce dernier est doté d’un repère cartésien d’origine O. À l’instant initial, A est situé au commet S de l’hémisphère et possède un vecteur vitesse v0 tangent à l’hémisphère. Dans tout l’exercice, on note g le champ de pesanteur ; g ~ 10 m. s −2 est sa norme. 1. Quelles sont les équations du mouvement de A ? Rn désigne la composante normale de la force de réaction du support hémisphérique. A est soumis à son poids et à l'action normale du support. 2. Quelles sont l’énergie cinétique, Ec, et l’énergie potentielle, Ep, de A ? Pour le calcul de cette dernière, la référence est prise à 0 en 𝑦 = 0. Ec = ½m (r j')2. Ep = mgy = mgr sin j. Réponses B et C. 3. Donner l’expression de la vitesse v de A en fonction de sa position. Seul le poids travaille et l'énergie mécanique reste constante. ½mv02 +mgr = ½mv2 +mgr sin j ; v02 +2gr = v2 +2gr sin j ; v2 =v02 +2gr(1-sin j) Réponse B. 4. Déduire de ce qui précède l’expression de la composante normale Rn de la force de réaction. Rn = -m r j'2 +mg sin j = mg sin j -m v2 / r. v2 =v02 +2gr(1-sin j). Rn =mg sin j -m / r [v02 +2gr(1-sin j) ] . Rn =mg sin j -m v02 /r -2mg +2mg sin j . Rn =3 mg sin j -m v02 /r -2mg . Réponse A. 5.  Quel est le sinus de l’angle j pour lequel A quitte la piste hémisphérique si v0 = 0. A quitte la piste dés que Rn s'annule. 3 mg sin j -m v02 /r -2mg = 0. 3 mg sin j  -2mg =0. 3  sin j  -2 =0. sin j  =2 / 3. Réponse C. Dans la suite de l’exercice, on prendra v0 = 0. 6.  Une fois le contact rompu, A évolue alors sans frottement dans le champ de pesanteur uniforme. Parmi les affirmations ci-dessous, identifier celles qui sont exactes. A) La trajectoire de A est rectiligne.  B) La vitesse de A selon l’axe Ox est nulle.  C) L’accélération de A possède deux composantes cartésiennes non nulles.  D) La vitesse de A lorsqu’il touche le sol est (2gr)½. Vrai. A est animé d'un mouvement de chute libre. L'accélération est dirigée selon la verticale descendante. La vitesse de A possède une composante selon chaque axe. Au contact avec le sol, la conservation de l'énergie mécanique donne : ½mv02 +mgr = ½mv2 avec v0 = 0. mgr = ½mv2 ; v2 = 2gr ; v = (2gr)½.

menu