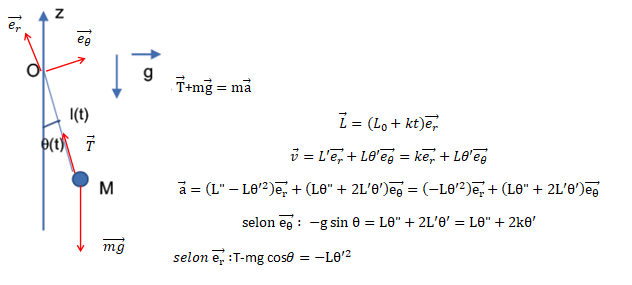Physique,
concours G2E ( Géologie, Eau, Environnement )2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
A.
Ascension et chute d'un sac de sable.
Une grue soulève verticalement un sac de sable de
masse m = 200
kg sur une hauteur h = 10 m. On néglige les frottements de l’air et on
choisira un axe vertical (Oz) ascendant, l’origine O étant au niveau du
sol. On donne l’accélération de la pesanteur g = 9,8 m.s−2.
1.Calculer le
travail du poids au cours de l’ascension et commenter son signe.
Travail résistant du poids en montée : W = -m g h = -200 x9,8 x10 =
-1,96 104 ~ -2,0 104 J.
2. Arrivé à la
hauteur h, le câble de la grue se rompt. Le sac tombe alors en chute
libre avec une vitesse initiale supposée nulle. A l’aide du théorème de
l’énergie cinétique, déterminer lavitesse v0 du sac assimilé
à un point matériel juste avant que celui-ci touche le sol. Faire
l’application numérique.
Travail moteur du poids en descente = m g h.
½mv02-0= mgh ; v02=2gh ; v0
= (2gh)½ =(2 x 10 x9,8)½ =14 m /s.
3.
Déterminer la loi horaire de la vitesse v(t) du sac et en déduire
l’expression de la durée de la chute libre puis sa valeur numérique.
Selon l'axe vertical ascendant : accélération : a =
-g ;
vitesse v(t) = -gt ( la vitesse initiale étant nulle).
t = |v| / g = 14 /9,8~1,4 s.
B. Mouvement pendulaire
d’un sac de sable.
Un sac de sable de masse m = 200 kg utilisé pour la construction de la
maison, assimilé à un point matériel M, est déplacé par une grue grâce
à un treuil (voir schéma ci-dessous). On néglige la masse du câble et
les frottements de l’air et on suppose que le système se comporte comme
un pendule simple de longueur variable, le câble étant enroulé sur le
treuil à vitesse constante. La longueur L du câble varie selon
l’équation horaire : L(t) =L0 + kt. k< 0 correspond au
cas où le sac remonte, k >0 correspond au cas où le sac descend. On
se place dans une base polaire d’origine O. On souhaite établir
l’équation différentielle vérifiée par q(𝑡) et commenter la solution
obtenue par analyse numérique.
4. Donner les expressions des
vecteurs position, vitesse et accélération dans la base choisie en
fonction de 𝑘, L(𝑡), q et q'.
5. Reproduire le
schéma ci-dessus et y indiquer les forces s’exerçant sur 𝑀.
6.
Exprimer la tension du câble en fonction de m, g, L(𝑡), q et q'
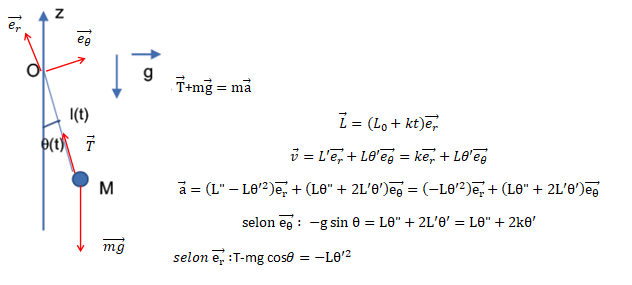
7. Dans le cadre
de petits mouvements (q
<< 1), montrer que l’équation différentielle vérifiée par q(𝑡) se présente sous la forme
canonique suivante :
q" +2k / L(t)q' + g/L(t)q=0.
sin q ~q radian ;
-g q = L q" +2kq' ; q" +2k / Lq' +g / L q= 0.
On donne ci-dessous l’allure de la courbe q(𝑡), obtenue après résolution
numérique de l’équation différentielle précédente pour 𝑘= −1 𝑚.𝑠−1
(remontée du sac de sable), q0
= 15°, L0 = 20 𝑚.
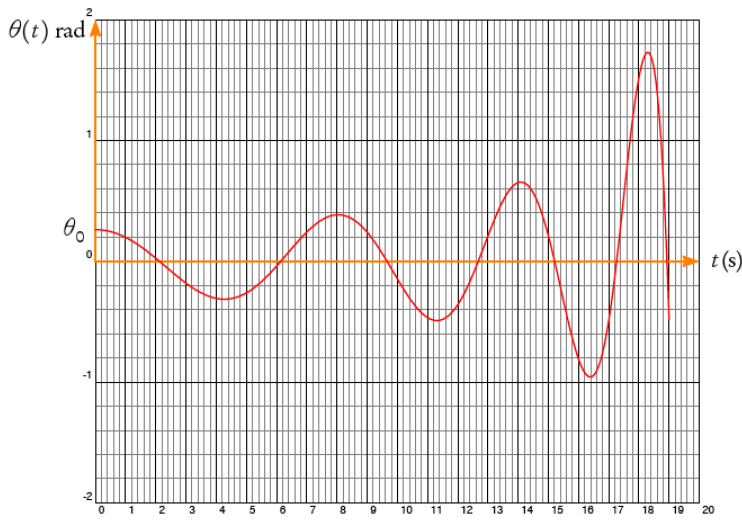
8. Calculer la tension du câble à
𝑡=0 𝑠.
T = mg cos q0 -L0
q'2
avec q'(t=0) = 0, la courbe
présentant un maximum.
T = 200 x9,8 x cos15=1,9 103 N.
9. A quel instant
la tension du câble est-elle maximale ? Commenter.
L(t) =20 -t.
T = 1,96 103 cos q
-(20-t)q'2.
1,96 103 cos q doit être maximum et (20-t)q'2doit être minimum.
Soit q = 0 et (20 -t)q'2 le plus petit possible soit q' nul.
C. Isolation thermique par
double vitrage.
L’isolation thermique de la maison met en jeu des fenêtres à double
vitrage. On cherche ici à comparer l’efficacité de l’isolation
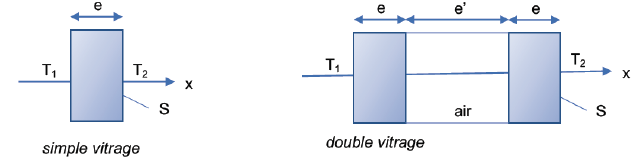
thermique par simple et par double vitrage. On considère dans un
premier temps, une plaque de verre d’épaisseur e = 4 mm et de
conductivité thermique lv
= 0,8 S.I. Les effets de bord seront négligés et on fera une étude
unidimensionnelle d’axe (Ox). La surface de la vitre perpendiculaire à
l’axe Ox est notée S. On négligera les transferts conducto-convectifs à
la surface du verre. On se reportera à la figure ci-dessous à gauche.
On suppose T1 > T2.
10. Ecrire la loi
de Fourier dans la symétrie du problème étudié en précisant la
signification des différentes grandeurs y intervenant. Interpréter le
signe figurant dans cette loi.
11.
Par analyse dimensionnelle, déterminer l’unité S.I. de la conductivité
thermique.
12.
On se place en régime permanent. Exprimer le flux thermique F traversant la vitre en fonction
de la différence de température D𝑇
de part et d’autre de la vitre, de lv
et des paramètres géométriques 𝑒 et 𝑆.
Le flux thermique à travers
une surface simple est : F
= lS (T1-T2)
/ e.
Flux en watt ; l conductivité
thermique en W m-1 K-1; S :
surface en m2 ; T1-T2 différence de
température en K ; e : épaisseur de la paroi en m. Le flux thermique va
du corps le plus chaud vers le corps froid.
13. Rappeler la
définition de la résistance thermique Rth d’un matériau et
préciser son unité.
Rth
= e / (lS)
exprimée en K W-1.
La résistance thermique indique la capacité de l'isolant à résister aux
variations de chaleur.
14.
Etablir l’expression de la résistance thermique Rth d’une
fenêtre simple vitrage en fonction de lv, e et 𝑆. Calculer 𝑅𝑡ℎ
pour 𝑆 = 4 m2.
Rth = 4 10-3 / ( 0,8 x4) = 1,25 10-3 K
W-1.
On s’intéresse maintenant à l’isolation par double vitrage « 4-16-4 »,
c’est à dire une vitre d’épaisseur 𝑒 = 4 mm, séparée par une couche
d’air sec d’épaisseur 𝑒’ = 16 mm d’une deuxième vitre d’épaisseur 𝑒 =
4 mm (voir figure ci-dessus à droite). La conductivité de l’air sec
vaut l𝑎 = 0,025
S.I.
15. Montrer que la
résistance thermique R'𝑡ℎ du double vitrage se met sous la
forme :
R'th=Rth(2+a)
où a est une constante à
exprimer en fonction de lv, l𝑎, 𝑒 et 𝑒’.
Conclure alors quant à l’efficacité de cette technique d’isolation.
R'th = 2e / (lvS)
+e'/(laS) ; Rth =
e/(lvS) ;
R'th = e / (lvS) [ 2+ e' lv / (ela)].
De plus en plus de maisons sont équipées de verres autonettoyants
(bioclean de Saint-Gobain par exemple) comportant des particules de
dioxyde de titane TiO2 semi-conducteur. Une lumière de
longueur d’onde adéquate permet d’arracher un électron à la couche
d’oxyde de titane (en le faisant passer de la bande de valence à la
bande de conduction). Ceci induit des phénomènes rédox à la surface du
TiO2 qui agit comme un catalyseur en dégradant les
salissures présentes sur le verre par production de radicaux hydroxyles.
La longueur d’onde maximale permettant d’arracher un électron est de
388 nm.
16. Rappeler les
deux modèles de description de la lumière et préciser lequel permet
d’expliquer l’existence d’une longueur d’onde maximale.
Modèle ondulatoire ( il explique les phénomènes de diffraction et
d'interférences) et modèle corpusculaire ( quantification de l'énergie
d'une onde).
17. Calculer, en
eV, l’énergie minimale à fournir pour arracher un électron à la couche
d’oxyde de titane.
E = h c / l = 6,62 10-34
x 3 108 / (388 10-9) =5,12 10-19 J
(3,2 eV).
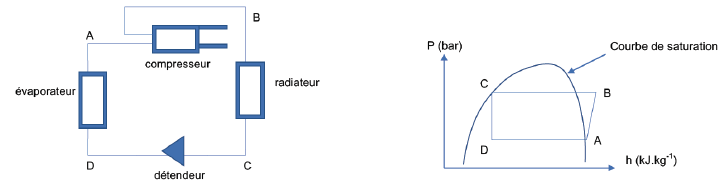
D Pompe à chaleur.
Pour maintenir la température de la maison constante, on utilise une
pompe à chaleur qui est une thermopompe à compression utilisant
l’ammoniac NH3 comme vapeur condensable (schéma ci-dessous).
Le cycle de transformations subi par le fluide est représenté dans le
diagramme de Mollier. (pression P en bar, en ordonnées et h enthalpie
massique en kJ.kg-1, en abscisses). Dans cette machine, le
fluide pris à l’état gazeux (vapeur juste saturante à la pression PA
et à la température q𝐴)
est comprimé de manière adiabatique jusqu’à l’état B (PB, q𝐵). Il est ensuite
refroidi puis entièrement liquéfié à pression constante (état C
correspondant au liquide juste saturant, température qC) dans un radiateur
au contact de l’air de l’habitation. Il traverse ensuite un détendeur
où il subit une détente isenthalpique qui ramène sa pression de PB
à PA. Il se trouve alors partiellement liquéfié (état D). Il
pénètre alors dans l’évaporateur (source froide) et se vaporise
complétement à la pression PA jusqu’au point A.
L’évaporateur et le radiateur ne possèdent pas de parois mobiles. On se
place en régime permanent. Dans les différents organes de la machine,
on négligera les variations d’énergie potentielle de pesanteur et
d’énergie cinétique.
Les données sont les suivantes :
Etat
|
P(bar)
|
q(°C)
|
h(kJ
kg-1)
|
A
|
3,5
|
-5
|
1760
|
B
|
15
|
|
1980
|
C
|
15
|
38
|
660
|
D
|
3,5
|
|
660
|
18. Rappeler la
définition de la pression de vapeur saturante.
Pression à laquelle la phase gazeuse d'une substance est en équilibre
avec sa phase liquide ou solide à une température donnée.
19. Donner la loi
de Laplace et rappeler ses conditions d’application. Calculer la
température qB au
point B.
Lors d'une transformation isentropique ( adiabatique réversible) : Tg P1-g = constante.
TB x PB1-g=TA x PA1-g ; TB =TA x (PA/ PB)1-g =(273-5)x(3,5/ 15)1-1,33 ~ 433 K( 160 °C).
20.
Reproduire sur la copie le diagramme (P,h) et
indiquer où se situe la courbe de rosée ainsi que la courbe
d’ébullition. Préciser l’état physique du système dans les différents
domaines. Quelle est la température qD
au point D ?
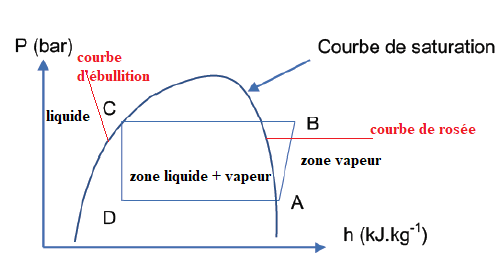
Détente isenthalpique de C à D : la pression varie et la température ne
change pas.
21. Rappeler
l’expression du premier principe sous forme de bilan enthalpique pour
les fluides en écoulement permanent (appelé encore premier principe
pour les systèmes ouverts ou encore « premier principe industriel ») en
précisant la signification physique des différents termes et appliquer
dans le contexte étudié.
La variation d'enthalpie d'un système ouvert est égale à la somme du
travail utile s'exerçant sur les parois mobiles et de la chaleur
échangée avec l'extérieur.
22. Déterminer les
variations d’enthalpie du système au sein de chaque organe de la pompe
à chaleur.
A --> B compresseur : 1980-1760=220 kJ.
B --> C radiateur : 660-1980=-1320 kJ.
C-->D détendeur : 660-660 = 0.
D --> A évaporateur : 1760-660 =1100 kJ.
23. Sachant que le
maintien de la température dans la maison impose une puissance de
chauffage Pth=10 kW, déterminer le débit massique Dm
d’ammoniac nécessaire.
dt = -QBC / Pth=1320
/ 10 =132 s
Dm = masse (1 kg ) / dt = 1 / 132 =7,6 10-3 kg /
s.
24. Calculer sur
un cycle, la puissance mécanique Pm=dW / dt reçue par le
fluide.
dW = 220 kJ ; dt = -QBC / Pth=1320 / 10 =132 s ; Pm
=220 /132~1,7 kW.
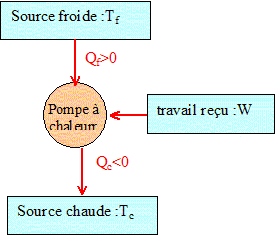
25. Expliquer à
partir d’un schéma où l’on symbolisera la pompe à chaleur et les
sources de chaleur chaude et froide, les échanges d’énergie Qc avec la
source chaude, Qf avec la source froide et W le travail échangé.
Préciser le signe de ses différentes grandeurs.
26.
Définir puis calculer l’efficacité e de la pompe à
chaleur.
coefficient
d’efficacité , notée e, ( réversibilité) : gain / dépense =|
chaleur cédéeau local |divisée par le travail reçu.
e = -Q c/ W = 1320 / 220 =6,0.
27.
Etablir l’inégalité de Clausius.
La variation d'entropie est nulle sur un cycle : Qc/Tc
+ Qf / Tf + Scrée = 0.
Dans le cas de l'irréversibilité : Scrée > 0.
Dans le cas de la réversibilité : Scrée
= 0.
Qc/Tc + Qf / Tf <
0.
28. Montrer que
l’efficacité de la pompe à chaleur est inférieure à une valeur maximale
emax que l’on calculera.
Efficacité maximale : chaleur cédée au local / travail reçu =Tc /
(Tc-Tf)
Température du local 19°C ou 292 K.
Température extérieure : -5 °C ou 268 K.
Efficacité maximale =292 / 24~ 12.
|
...
|
....
|
Etude du rendement
d'une éolienne.
La demande énergétique domestique va augmenter suivant les prévisions,
de 50 % d’ici à 2050. Ceci est lié à l’électrification croissante des
habitats (augmentation du nombre d’appareils électriques, mise en place
de bornes pour recharger les voitures électriques…). Il s’agit donc
d’augmenter la production d’électricité en développant les différentes
sources d’électricité possibles dont l’éolien qui produit aujourd’hui
environ 6% de la consommation nationale. On s’intéresse dans cette
partie à l’étude du rendement d’une éolienne. On rappelle qu’une
éolienne est un dispositif qui transforme l’énergie cinétique du vent
en énergie mécanique, le plus souvent transformée ensuite en énergie
électrique. L’éolienne de surface S est située à l’origine O d’un axe
Oz horizontal. La figure ci-dessous montre l’écoulement d’air de part
et d’autre de l’éolienne.
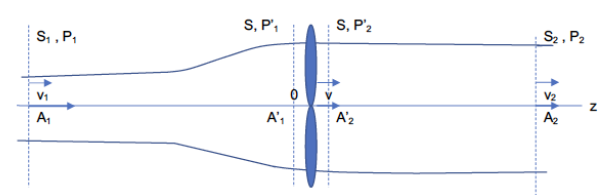
On note v1
et v2 la vitesse du vent en amont et en aval de l’éolienne.
On suppose également que la pression est égale à la pression
atmosphérique P0 sur ces deux surfaces S1 et S2.
On se place dans les conditions d’application de la relation de
Bernoulli. On note µ la masse
volumique de l’air.
29. Rappeler la
relation de Bernoulli et ses hypothèses d’application.
Pour un écoulement incompressible, parfait et stationnaire :
expression du théorème de Bernoulli en régime
stationnaire : p + ½µv2 + µgh = Cste.
On considère
une ligne de courant où figure quatre points : A1 loin de
l’éolienne en amont, A'1 immédiatement avant l’éolienne, A'2
immédiatement après et A2 loin de l’éolienne en aval.
30. Justifier, à
l’aide de la conservation du débit volumique qu’il ne peut y avoir de
discontinuité de la vitesse au niveau de l’éolienne. On notera v cette
vitesse.
En A'1 : Q = S v'1 ; en A'1 : Q = S v'2
; la conservation du débit volumique conduit à v'1 =v'2
= v.
C’est donc une
discontinuité de pression de part et d’autre de l’éolienne qui permet
son fonctionnement.
31. Ecrire la
relation de Bernoulli entre A1 et A′1 puis entre A2 et A′2. Pourquoi ne peut-on pas écrire
la relation de Bernoulli entre les points A′1 et A′2
?
Le vent étant horizontal : P0 + ½µv12
= P'1 +
½µv2 .
P0
+ ½µv 22 = P'2 + ½µv2 .
Entre A'1 et A'2 se trouve l'éolienne, l'énergie
de l'air n'est pas conservée.
32. En déduire l’expression de la
différence de pression P′1−P′2 en fonction de µ, v1
et v2.
P′1−P′2
=½µv12 -½µv 22.
33. La force exercée par le vent sur
les pâles de l’éolienne vaut F = (P′1−P′2).S. En
déduire la puissance P développée par cette force sur les pâles.
F = ½µS(v12-v22). P = F v =½µS(v12-v22)
v.
34. On peut montrer que v =0,5 (v1
+ v2). En déduire une nouvelle expression de P en fonction
de v1, v2, S et µ.
P = 0,25µS(v12-v22)(v1 + v2).
On définit le
rendement r de l’éolienne comme le rapport entre la puissance P
précédente et la puissance de l’énergie cinétique du vent Pcin 1
(non perturbé par la présence de l’éolienne, de vitesse v1,
de débit massique Dm,1 et traversant S) : r =P / Pcin1.
35. Exprimer
l’énergie cinétique élémentaire dEc,1 d’une particule de
fluide de vitesse v1 et de masse élémentaire dm.
dEc,1=½dm v12.
36. En déduire
l’expression de Pcin1= dEc,1 / dt en fonction de Dm,1 et v1 puis en
fonction de v1, S et µ.
Pcin1=½dm v12 /
dt ; Dm,1 = dm / dt ; Pcin1=½Dm,1 v12 .
Dm,1=µ
S v1 ; Pcin1=½µS v13 .
37. En déduire que le rendement de l
‘éolienne s’écrit : r = ½(1−x2)(1+x) avec x =v2/ v1.
P / Pcin 1
=0,25µS(v12-v22)(v1 + v2)
/ (½µS v13 ) =½(v12-v22)(v1 + v2) / v13 .
r =½(1-x2)(1+x).
38. Déterminer la valeur xmax
conduisant au rendement maximal puis calculer le rendement maximal.
On dérive r en posant u = 1-x2 et v = 1+x ; u' = -2x ; v' = 1.
u'v+v'u = -2x(1+x) +1-x2
=1-2x-3x2.
Solutions de 1-2x-3x2
=0.
Discriminant D
=4+12=16=42.
Solution positive retenue : (2-4)/(-6) =1 /3.
rmax =0,5(1-1/9) 4 /3 =0,59.
F. Etude d'une fibre
optique.
Grâce à sa simplicité d’installation, sa discrétion et sa fiabilité, la
fibre optique apparaît de plus en plus dans les habitations pour la
transmission de données numériques. On étudie ci-dessous une fibre
optique à « saut d’indice » constituée d’un coeur cylindrique en silice
de rayon a et d’indice n1, entouré d’une gaine en silicone
d’indice n2 et de rayon extérieur b. Les faces d’entrée et
de sortie sont perpendiculaires au cylindre d’axe Oz formé par la
fibre. L’ensemble, en particulier la face d’entrée, est en contact avec
l’air d’indice nair = 1,0.
On considère un rayon incident sur le coeur et contenu dans le plan Oxz
(voir figure ci-dessous). On note i l’angle d’incidence.
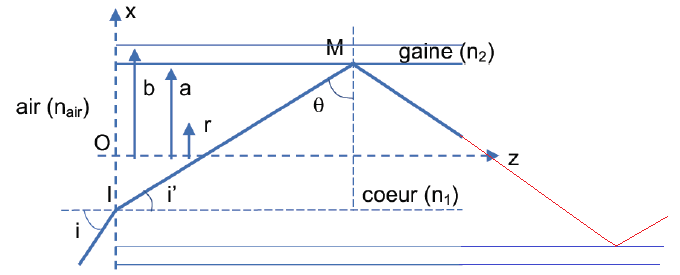
39. Quel est le
phénomène physique se produisant en I ? Quel est celui se produisant en
M ? Poursuivre sur votre copie le tracé du rayon lumineux dans la fibre.
En I : réfraction ; en M : réflexion totale.
40. Enoncer les
lois de la réfraction de Snell-Descartes. On s’appuiera de même sur un
schéma définissant les différentes grandeurs.
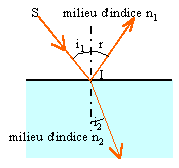
Les trois rayons incident, réfléchi et
réfracté sont dans le même plan ;
l'angle d'incidence i1 est égal à
l'angle de réflexion r. Les angles d'incidence
i1 et réfracté i2 sont
reliés par la relation : n1 sin
i1 = n2 sin
i2.
41. A quelles conditions un rayon lumineux subit-il une réflexion
totale sur un dioptre séparant un milieu incident d’indice n1 et un
milieu d’indice n2 ? Il est attendu une condition concernant les
indices optiques et une autre concernant l’angle d’incidence.
Lors du passage de la lumière d'un milieu d'indice n1 à un milieu d'indice n2 < n1, il existe un angle d'incidence limite ilim au dela duquel le rayon réfracté n'existe plus : seul le rayon réfléchi existe.
n1 sin
i1 = n2 sin i2 et
|sin i2| inférieur ou égal à
1.
n1 sin
ilim = n2 soit sin ilim = n2 /
n1 avec n2 < n1.
42. Déterminer en fonction en fonction de de 𝑛1 et 𝑛2 la condition
sur l’angle i pour que le rayon ait une propagation guidée dans le
coeur ?
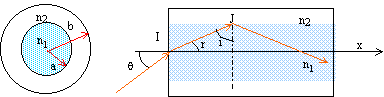 en I, dioptre air/coeur :
nair sin qi
= n1 sin r ; sin qi
= n1 sin r
(1).
en J, il y a réflexion
totale : sin ilim = n2 /
n1 ; les angles i et r sont
complémentaires soit sin r = cos i.
(1) donne : cos i = sin q / n1 ; sin q = n1 cos i ; sin qlim = n1 cos ilim ;
q doit donc être inférieur à qlim. 43. On appelle ouverture numérique du guide (O.N.) la quantité O.N.= sin i𝑚𝑎𝑥 où imax est la valeur maximale de l’angle i. Exprimer O.N. en fonction de n1 et n2.
O.N = sin qlim = n1 cos ilim.
De plus sin ilim =n2/n1.
cos2ilim = 1 -sin2ilim=1-(n2/n1)2.
O.N=n1[1-(n2/n1)2]½ =(n12-n22)½.
44. Calculer imax et O.N. pour n1=1,456 et n2=1,410.
sin ilim =n2/n1 = 1,410 / 1,456=0,9684 ; ilim =75,6 °.
O.N = (1,4562-1,4102)½=0,363.
45. On considère dans cette question une fibre à gradient d’indice «
parabolique » : dans le coeur, l’indice varie suivant la loi
n(r)=(n1−(n1−n2)r2/ a2), r étant la distance d’un point du coeur à
l’axe Oz. Tracer schématiquement et en justifiant, le rayon lumineux
dans le coeur. On pourra considérer le coeur comme un empilement de
couronnes concentriques d’indice lentement variable.
L'indice
de réfraction varie progressivement du centre vers la surface
extérieure de la fibre. On peut modéliser la fibre par un assemblage de
strates concentriques d'indice de réfraction légérement différents :
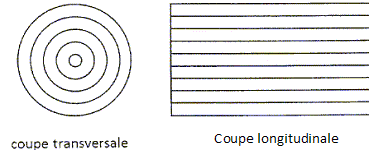
Un
rayon lumineux se propage en ligne droite dans chaque strate, il subit
une réfraction à chaque changement de strate. Quand son incidence est
trop élevée, il subit une réflexion totale, ce qui lui permet de rester
dans la fibre, comme le montre la figure ci-dessous :
G. Ecoulement de la peinture sur un mur.
On cherche à peindre les murs d’une pièce rectangulaire de la maison de
dimension longueur 6 m × largueur 4 m × hauteur 2,5 m avec 2 couches
d’une peinture dont le pouvoir couvrant vaut 12 m2 pour un litre de peinture.
46. Quel est le nombre de pots de peinture de volume 1,5 L nécessaires ?
Surface des murs S =2 (largeur + longueur) x hauteur =2 x 10 x2,5 = 50 m2.
50 / 12 =4,17 L pour une couche soit 8,3 L pour deux couches.
8,3 / 1,5 ~5,6 ( 6 pots).
47. Déterminer l’épaisseur de la couche de peinture déposée pour une couche de peinture appliquée.
S e = 4,17 10-3 m3 ; e =4,17 10-3 / 50=8,3 10-5 m =0,083 mm.
La peinture est assimilée à un fluide de viscosité dynamique h = 0,12 Pℓ et de masse volumique µ = 1,2 kg.L−1 ( 1,2 103 kg m-3)
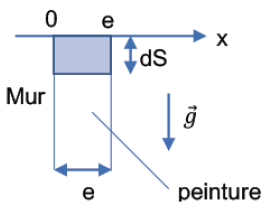
On s’intéresse ici à la résistance de la peinture aux coulures. On
considère une couche de peinture d’épaisseur e appliquée sur un mur
vertical. L’écoulement est modélisé par un écoulement Couette plan de
gradient de vitesse égale à 10 s−1. On travaille sur une
particule fluide définie entre x=0 et x=e et de surface dS. On note g
l’accélération de la pesanteur. On donne e = 0,080 mm.
48. Préciser l’unité S.I. de la viscosité dynamique.
Pascal seconde ( Pa s).
49. Calculer la vitesse de l’écoulement à l’interface peinture/air.
dv /dx = 10 ; v = 10 x +Cste.
La vitesse étant nulle en x=0, v(x) = 10 x.
v(e) =10 e = 10 x 8,0 10-5 = 8 10-4 m /s.
50. Définir puis calculer le nombre de Reynolds pour le problème étudié et conclure sur la nature de l’écoulement.
Ce nombre caractérise l'écoulement et en particulier la nature de son régime.
Re = U h / n.
U : moitié de la différence de vitesse entre les deux parois.
h : moitié de la distance entre les deux parois.
n : viscosité cinématique du fluide = viscosité dynamique / masse volumique =0,12 / 1200 =1 10-4 m2 s-1.
Re =4 10-4 x 4,0 10-5 / 10-4=1,6 10-4.
Re << 1, écoulement laminaire.
51. Exprimer la contrainte s exercée par la force de pesanteur sur la
particule fluide en fonction de µ, e et g. En supposant que la
peinture n’offre pas de résistance aux coulures, exprimer le gradient
de vitesse dv / dx lié aux coulures. On constate que lors du
séchage qui suit l’application aux murs, la viscosité de la peinture
augmente. Quel est l’intérêt ?
La peinture présente en fait une résistance aux coulures et se comporte
comme un fluide à seuil de Bingham : tant que la contrainte s
appliquée à la peinture est inférieure à une contrainte seuil s𝑆 >
0, celle-ci ne s’écoule pas ; si la contrainte dépasse s𝑆, la
peinture a un comportement de fluide visqueux newtonien. On a :
s < sS : dv/dx=0.
s > sS : s = sS +hdv/dx=0.
52. Représenter graphiquement la contrainte s en fonction du gradient de vitessė.
53. Dans l’exemple étudié ici, déterminer la contrainte seuil minimale s𝑆,𝑚𝑖𝑛 pour laquelle il n’y a pas de coulures.
54. Calculer s𝑆,𝑚𝑖𝑛.
|
|