Chimie,
mathématiques,
Concours technicien police scientifique, zone est 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Chimie.
1- La densité d’un gaz est mesurée
par rapport ... (1pt)
A – à l’eau
B – à l’oxygène
C – à l’air. Vrai.
D – au dioxyde de carbone.
2- La densité d’un
liquide est mesurée par rapport ... (1pt)
A – à l’eau. Vrai.
B – à l’oxygène
C – à l’air
D – à l’huile.
3- Lors de la
dilution d’une solution A, le nombre de moles de A est ... (1pt)
A – diminué. Vrai.
B – augmenté
C – constant.
4- Pour être
utilisée comme support de titrage d’une solution, la réaction doit être
: (1pt)
A – lente
B – rapide. Vrai.
C – totale. Vrai.
D – partielle.
5- Le produit
ionique de l’eau appelé Ke à 25°C est égal à : (1pt)
A – Ke = 1x10-7
B – Ke = 2x10-7
C – Ke = 1x10-14.
Vrai.
D – Ke = 2x10-14.
6- Ke est la
constante d’équilibre de la réaction : (1pt)
A – HA+ H2O <=> A- + H3O+
B – 2 H2O
<=> H3O+
+ HO-. Vrai.
C 2 H2O => H3O+ + HO-.
7- A concentration
égale, la solution qui correspond à la base la plus forte : (1pt)
A – est celle qui a la valeur du pH la plus grande. Vrai
B – est celle qui a la valeur du pH la plus petite
C – est celle qui a la valeur du pKA la plus grande. Vrai
D – est celle
qui a la valeur du pKA la plus petite.
8- Une espèce chimique capable d’accélérer une transformation
chimique sans en modifier les produits est : (1pt)
A – un réactif
B – un propulseur
C – un amphotère
D – un catalyseur. Vrai.
9- Une molécule
d’alcool possède un groupe : (1pt)
A – carbonyle
B – carboxyle
C – hydroxyle. Vrai.
D – amine.
10- Une molécule de
la famille des amides a la formule semi-développée de la forme : (1pt)

11- On veut
déterminer la valeur de la constante d’acidité de l’acide nitreux.
(4pts)
a – Ecrire
l’équation de la réaction de l’acide nitreux avec l’eau
HNO2 aq + H2O(l) = H3O+aq +
NO2-aq.
b – Dans une
solution d’acide nitreux, on détermine les concentrations suivantes :
[HNO2 ] = 1,9 x 10-4 mol.L-1 et [H3O+] = 3,1 x 10-4 mol.L-1.
Déterminer la valeur de la constante d’acidité KA du couple HNO2
/ NO2-.
KA = [H3O+][NO2-] / [HNO2] =3,1 x 10-4 x 3,1 x 10-4 / (1,9 x 10-4) =5,06 10-4.
c – En déduire son pKA.
pKA = - log (5,06 10-4) =3,3.
12- ( erreur dans le texte initial, remplacer 121 000 par 78 000 ainsi que les pourcentages ou bien conserver les nombres mais ce
n'est pas le polychlorure de vinyle).
Le PVC (Polychlorure de vinyle) est un polymère contient 56,7 % en
masse de chlore, 38,4% en masse de carbone, et 4,9 % en masse
d’hydrogène.
Les macromolécules de ce polymère ont une masse molaire moyenne de 78
000 g.mol-1 pour une degré de polymérisation de n=1250.
Données : masses molaires atomiques M(C)=12 g.mol-1 , M(H)=1
g.mol -1, M(Cl)=35,4 g.mol-1.
(6pts)
a - Déterminer la
masse molaire puis la formule brute du monomère de ce plastique. (3pts)
CxHyClz.
12 x / 38,4 = y /2 = 35,4 z / 56,7 = M / 100.
M = 78 000 / 1250 =62,4 g / mol.
x = 0,624 x38,4 / 12 ~2.
y =0,624 x4,9 / 1 ~3.
z =0,624 x56,7 / 35,4 ~1.
C2H3Cl.
b – En déduire la formule
semi-développée de ce monomère. (1pt)
H2C=CHCl.
c – Déterminer le
nom de ce monomère. (1pt)
Chloroéthène ou chlorure de vinyle.
d – Ecrire
l’équation-bilan de la réaction de polyaddition. (1pt)
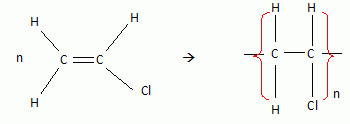
|
...
|
....
|
Mathématiques.
Exercice 1 : Probabilités
– 3 points
Lors d’un concours administratif, les candidats doivent choisir une
épreuve obligatoire entre deux matières, mathématiques ou chimie.
Ils ont également la possibilité de choisir une langue vivante, de
manière optionnelle.
Parmi les candidats, 54 % ont choisi les mathématiques, et 32 % de ceux
qui ont choisi les mathématiques ont également pris l’option langue
vivante.
Un premier candidat se présente devant le jury.
Déterminer la probabilité que le candidat ait choisi la dominante
chimie et l’option langue vivante.
100-54=46 % ont choisi la chimie.

Il manque une information
dans le sujet ( par exemple, le pourcentage de candidats ayant choisi
une option langue vivante).
Exercice 2 : Suites
– 3 points
Le directeur d’un laboratoire souhaite effectuer une enquête de
satisfaction auprès de ses clients. La première année, seulement 20 %
s’avèrent satisfaits. Le laboratoire travaille alors à améliorer ses
résultats et espère une augmentation de 5 points par an.
Au bout de combien d’années d’enquête le directeur espère-t-il obtenir
100 % de satisfaction ?
u0 = 20 ; u1 = u0 x1,05 ; un
= u0 x1,05n .
20 x1,05n = 100 ; 1,05n =5.
n ln(1,05) = ln(5) ; n ~ 32,98 soit 33.
Exercice 3 -Fonctions
– 8 points
1- Soit f la
fonction définie sur l’intervalle [0 ; 8] par :
f(x)=0,5 x3-12 x2+65,625 x+20.
Déterminer f ’(x) pour tout réel x appartenant à l’intervalle [0;8] et
montrer que f ’(x) =(x - 3,5)(1,5 x – 18,75).
f '(x) = 0,5 * 3 x2 -12 *2 x+65,625.
f '(x) = 1,5 x2-24x+65,625.
Solutions de 1,5 x2-24x+65,625 = 0.
D =242-4 *1,5*65,625=182,25=13,52.
Solutions x1 = (24-13,5) /3 =3,5 et (24+13,5) /3 =12,5.
f '(x) = 1,5 (x-3,5)(x-12,5) = (x - 3,5)(1,5 x – 18,75).
2- Étudier le signe
de f ’(x) puis en déduire le tableau de variations de f.

3- La concentration
limite d’un résidu de pesticide dans l’eau de consommation a été fixée
à 50
mg.L-1. Suite à une suspicion d’épandage illégal de ce
pesticide, des tests sont effectués sur un
captage d’eau pendant 8 jours. Soit f la fonction qui modélise le taux
de résidu du pesticide, x jours
après le début des tests,
• Quel sera le taux maximal de résidu de pesticide atteint durant ces 8
jours ?
• Quel sera le taux de de résidu attendu à 8 jours ?
Exercice 4 – Loi uniforme
- 6 points
Une perquisition est demandée par un service d’enquête, avec demande
d’assistance de la Police Scientifique entre 18h30 et 20h45, sans
confirmation de l’heure exacte. Un seul effectif est positionné en
astreinte pour répondre aux diverses demandes.
Une seconde intervention était déjà programmée pour effectuer des
constatations à l’occasion d’une découverte de personne grièvement
blessée.
Quelle est la probabilité que la perquisition ait lieu en même temps
que les constatations qui dureront de 19h à 19h30 ?
18 h 30 : a =0 ; 20 h 45 ; b = 2,25 ; 19 h : c = 0,5 ; 19 h 30 : d = 1.
Probabilité que la perquisition ait lieu en même temps que les
constatations :(d-c) / (b-a) = 0,5 / 2,25~0,22.
|
|