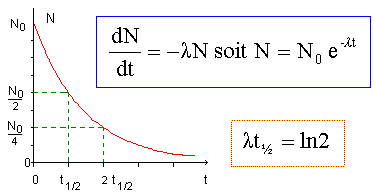Mathématiques,
sciences, concours technicien de la police technique et
scientifique 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Mathématiques
Exercice 1 ( 12 points) .
Un
technicien doit intervenir sur 4 constatations successives suite à des
faits de cambriolages. A chaque mission, il a une probabilité p = 0,25
de relever au moins une trace papillaire sur les surfaces manipulées
par les auteurs. Cette probabilité reste fixe pour chaque mission, quel
que soit le résultat de la mission précédente.
1. Comment
appelle-t-on l'expérience aléatoire d'une unique mission telle qu'elle
est décrite ci-dessus ? Définissez une variable aléatoire X
correspondant à cette expérience et donner la loi de probabilité
associée.
Chaque constatation est indépendante des autres et deux issues sont
possibles : relever au moins une trace ou bien ne relever aucune
trace. Soit X une variable aléatoire suivant la loi binomiale de
paramère p = 0,25 et n = 4.
2. Soit Y la variable aléatoire indiquant à l'issue des 4 constatations
le nombre de missions ayant donné lieu à la révélation d'au moins une
trace papillaire sur les surfaces manipulées par les auteurs. Quelle
loi suit cette varaible aléatoire et quels sont ces paramètres ?
Y suit la loi binomiale de paramètres p = 0,25 et n = 4.
3. Donner l'arbre
de probabilités représentant la succession des 4 missions, les issues
possibles et la pondération par les probabilités de chaque issue.
4. En
utilisant cet arbre, donner la probabilité de l'événement A " aucune
trace papillaire n'a été relevée à l'issue des 4 missions". Conclure
sur les chances de trouver au moins une trace papillaire à l'issue des
4 missions. 
p(A) = 81 / 256 ~0,316.
Probabilité de trouver au moins une trace = 1 - P(A) = 175 / 256 ~ 0,684.
5. Retrouver ce résultat en exprimant P(Y=1), P(Y=2), P(Y=3) et P(Y=4) à l'aide des coefficients binomiaux.
P(Y=1) =(4 1) x0,25 x0,753 ~0,422.
P(Y=2) =(4 2) x0,252 x0,752 ~0,211.
P(Y=3) =(4 3) x0,253 x0,75 ~0,047.
P(Y=4) =(4 4) x0,254 x0,750 ~0,004.
P(Y=1) +P(Y=2) +P(Y=3) +P(Y=4) =0,683.
Exercice 2 (8 points). Soit u la suite numérique réelle définie par u 0 = 0,5 et u n+1 = u n2 -u n+1.
1. Calculer u 1 et u 2 et indiquer quelles conjectures vous pouvez faire sur la monotonie et la convergence de u.
u 1 = 0,5 2 -0,5 +1 = 0,75.
u2 = 0,752 -0,75 +1 = 0,8125.
La suite est monotone et croissante.
2. Considérons la fonction f définie sur [0 ; 1] par f(x) =x2-x+1. Etudier les variations de f.
f '(x) = 2x-1.
Si x > 0,5, f(x) est strictement croissante.
Si x < 0,5, f(x) est strictement décroissante.
Si x = 0,5, f(x) présente un minimum : f(0,5) = 0,75.
3. Montrer que 0 < un < 1.
un+1 =f(un).
Initiation : u0 = 0,5 la propriété est vraie au rang zéro.
Hérédité : 0 < un < 1 est supposée vraie.
f(x) est croissante sur [0,5 ; 1] :
f(0,5) < f(un ) < f(1).
0,75 < un+1 < 1.
0 < un+1 < 1. la propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est vraie pour tout n entier naturel.
4. Montrer que u est croissante et en déduire qu'elle converge.
un+1 -un =u2n - 2un +1=(un-1) 2 > 0.
La suite est croissante et u0 = 0,5.
0 < un < 1. La suite est bornée par 1.
Donc la suite converge vers 1.
Chimie
Exercice 1 (7 points)
1. Déterminer
la formule brute, la formule semi-développée et la formule topologique
de la molécule suivante : 2-cyanoprop-2-ènoate de méthyle.
2. Combien de groupement fonctionnels cette molécule possède t-elle ? Donnez leurs noms.

3. Déterminer sa masse molaire. M = 111 g / mol.
4. En présence d'eau, cette molécule forme une longue chaine moléculaire.
a. Comment appelle t-on ce type de réaction ?
Polymérisation ; le 2-cyanoprop-2-ènoate de méthyle est le monomère.
b. L'humidité favorise cette réaction, quel anion est susceptible de l'initier et pourquoi ?
c. Quelle propriété découle de cette réaction ?

L'ion hydroxyle HO- joue le rôle de nucléophile.
Exercice 2. (10 points).
On considère une solution d'acide éthanoïque V = 10 mL, c =0,1 mol / L, pH = 2,9.
On donne 10-0,1 ~1,26 ; 1,262 ~1,59.
1. Quelle est la formule chimique de cet acide ? Donnez le nom et la formule de sa base associée.
CH3-COOH ; CH3-COO- ion éthanoate.
2. Ecrire l'équation de la réaction de cet acide avec l'eau et donner le tableau d'évolution de la réaction.
CH3-COOH aq + H2O(l) = CH3-COO- aq +H3O+aq.
état
|
avancement (mol)
|
CH3-COOH aq |
+ H2O(l) |
=CH3-COO- aq |
+H3O+aq. |
initial
|
0
|
10-3
|
solvant
|
0
|
0
|
final
|
xf=10-pH V=10-2,9 x 0,01~1,26 10-5
|
10-3-xf =9,87 10-4
|
xf |
xf |
3. Calculer la constante d'acidité Ka.
Ka = [CH3-COO- aq] [H3O+aq] / [CH3-COOH aq] =xf2 /((1-xf) V)=(1,26 10-5)2 / (9,87 10-6 )=1,6 10-5.
4. En déduire le pKa.
pKa = - log(1,6 10-5) ~4,8.
5. Tracer le diagramme de prédominance et indiquer quelle espèce prédomine en solution.
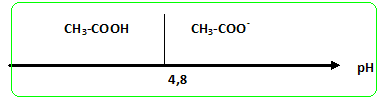
A pH inférieur à pKa, la forme acide CH3COOH prédomine.
6. Que se passe t-il si la quantité initiale d'acide éthanoïque vaut n0=2,52 10-5 mol ?
.
état
|
avancement (mol)
|
CH3-COOH aq |
+ H2O(l) |
=CH3-COO- aq |
+H3O+aq. |
initial
|
0
|
2,52 10-5
|
solvant
|
0
|
0
|
final
|
xf
|
2,52 10-5-xf
|
xf |
xf |
1,6 10-5 =xf2 /((2,5210-5-xf) V)=xf2 /((2,5210-5-xf) 0,01).
1,6 10-7 (2,5210-5-xf) =xf2 .
xf2 +1,6 10-7 xf -4,0 10-12 =0.
Discriminant = (1,6 10-7)2 +4*4 10-12 ~1,6 10-11 ~(4 10-6)2.
xf = (-1,6 10-7 +4 10-6) / 2 ~1,9 10-6 mol.
[ H3O+aq]= 1,9 10-6 / 0,01 =1,9 10-4 ; .pH =3,7.
ou plus simplement : Ka ~ xf2 / (n0V).
xf2 ~Ka n0 V=1,6 10-5 x 2,52 10-7 ~4 10-12 ; xf ~ 2 10-6 mol.
|
...
|
....
|
Exercice 3 (3 points)
1) Qu'est ce qu'un isotope ?
Deux isotopes ne diffèrent que par leur nombre de neutrons. Ils ont le même numéro atomique Z.
126C ( 6 protons et 6 neutrons) et 146C ( 6 protons et 8 neutrons).
2) Définissez les deux types de radioactivité ß.
ß- : émission d'un électron 0-1e; ß + émission d'un positron 01e.
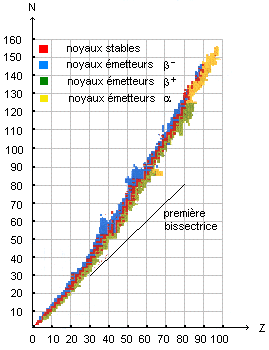
3) Quel est le lien entre la position d'un noyau sur le diagramme ( N, Z) et les deux types de radioactivités précédentes ?
4) Qu'est ce que la décroissance radioactive et en cinétique de réaction chimique de quoi est-elle l'analogue ?
En cinétique chimique, réaction d'ordre 1.
Soit un échantillon contenant N0 noyaux
radioactifs à la date t0 =0 choisie comme
date initiale. Soit N le nombre de noyaux radioactifs (non
désintégrés) encore présents
dans l'échantillon à la date t.
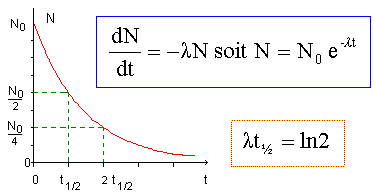
l est la constante
radioactive, caractéristique d'un
radioélément.
La demi-vie radioactive,(ou période)
notée t½, d'un échantillon de noyaux
radioactifs est égale à la durée au
bout de laquelle la moitié des noyaux radioactifs
initiaux se sont désintègrés.
5. On considère la
désintégration alpha d'un échantillon d'uranium 238 en thorium 234
ayant une activité initiale de 98 000 Bq et une constante radioactive l = 4,9 10-15 s. Ecrire l'équation de désintégration et déterminer le nombre initial de noyaux instabmes dans l'échantillon.
23892 U--> 23490 Th +42 He
N= A / l = 98 000 / (4,9 10-15)=2,0 1019 noyaux.
|
|