Mathématiques, concours Police Technique et Scientifique 2021. ( zone Ouest) En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Question 1 :   2 points. On considère la suite géométrique (un) telle que u0 = -5 et q = 3. La valeur de la somme S = u0 +u1 +... +u9 est : A. 148 001 ; B. 150 000 ; C. -147 500. D. -147 620 Vrai S = u0 (1-q10) / (1-q) =-5 (1-310) /(1-3) =147 620. Question 2 : 4 points. 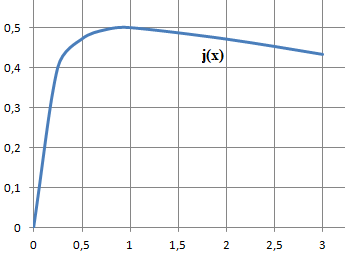Soit j définie sur [0 ; +oo[ par j(x) = x½ / (x+1). Déterminer le signe de la dérivée de cette fonction. On pose u = x½, v = 1+x ; u' = ½x-½ ; v' = 1. (u'v-v'u) / v2 = [(x+1)½x-½- x½ ] / (1+x)2. Le signe de la dérivée est celui du numérateur :(x+1)½x-½- x½ = x½[(x+1)  /(2x) -1) =x½[(1-x) / 2x] x-½ et x sont positifs ; si x appartient à [0 ; 1[, j '(x) > 0 ; si x = 1; j '(x) = 0 ; si x > 1; j'(x) < 0. Question 3 : (8 points) Le nombre d'habitants d'une région est donné par la fonction f(t) = 12 exp(0,05 t) exprimée en millions d'habitants pour l'année 2000 +t. 1. A partir de quelle date la population aura-t-elle triplée ? f(0) = 12 ; 3 f(0) = 36 = 12 exp(0,05 t). 3 =exp(0,05 t) ; ln(3) =0,05 t ; t ~22. (année 2022). 2. Cette région ne  peut pas nourrir plus de 20 millions de personnes. Pendant combien d'années après 1990, la nourriture sera t-elle suffisante ? f(t) = 12 exp(0,05(-10) = 20. 20 /12 = exp(0,05 t) ln(20 / 12) = 0,05 t ;  t ~ 10. (année 2010). Réponse (20 ans). ... .... Question 4 : (12 points) L'azote de l'atmosphère est transformé en carbone 14 radioactif sous l'effet du rayonnement cosmique. Les êtres vivants contiennent du carbone 14 qui est renouvelé constamment. A leur mort, il n'y a plus d'emprunt de 14C à l'extérieur et le 14C qu'ils contiennent se désintègre. Le temps écoulé depuis la mort d'un ête peut être évalué en mesurant la proportion de carbone 14 qui lui reste. Soit N(t) le nombre d'atomes de 14 C à la date t exprimée en années.. La vitesse de désintégration est proportionnelle à N(t) : dN(t) dt= -0,0001238 N(t). 1. En appelant N0 le nombre d'atomes de 14C initial, démontrer que N(t) = N0 exp(-0,0001238 t) dN(t) dt +0,0001238 N(t) =0. Solution de cette équation différentielle : N(t) = A exp(-0,0001238 t) avec A une constante. N(t=0) = N0 = A. N(t) = N0 exp(-0,0001238 t). 2. Quel est le  pourcentage d'atomes de carbone 14 perdu au bout de 20 000 ans. N(t= 20 000 )= N0 exp(-0,0001238 x20 000) =0,084 N0. 1-N(t=20 000) / N0 =1-0,084 =0,916 ( 91,6 %). 3. On appelle période ou demi-vie du 14 C le temps au bout duquel la moitié des atomes se sont désintégrés. Déterminer la période du carbone 14. 0,5 N0 = N0 exp(-0,0001238 t½). ln (0,5) = -ln(2) =-0,0001238 t½. t½ =5 599 ans. 4. On analyse des fragements d'os trouvés dans une grotte. Ils ont perdu 30 % de leur teneur en carbone 14. Déterminer l'âge du fragment d'os. 0,70 N0 = N0 exp(-0,0001238 t). ln(0,70) = -0,0001238 t. t =2 881 ans. Question 5 : (4 points) Dans un pays 10 % des plages sont atteintes par des algues toxiques. On modifie le processus de rejet chimique puis on prend un échantillon aléatoire de 150 prélèvements et on constate que 18 présentent des traces d'algues toxiques. Ce nouveau traitement a -t-il un impact sur le pourcentage de plages polluées ? 18 / 150 = 0,12 (12 %). Ce nouveau traitement n'a pas d' impact sur le pourcentage de plages polluées .

menu