Question
1 : Soit (un) une suite géométrique de raison 3 et de premier terme u0 = 21.
La somme S= u0+u1+u2+…+u5 est égale à
A. 6542 ; B. 2541 ; C. 7644. Vrai
S = u0 (1-q6) / (1-q) =21 (1-36) /(1-3) =7644.
Question 2 : Soit pour tout x de R, f(x) = ln(x
2+1)-x , alors :
A) f est croissante sur R
B) La limite de f en plus l'infini est plus l'infini.
C)
La limite de f en moins l'infini est plus l'infini. Vrai
f '(x) =2x / (x2+1) -1=(2x-x2-1) / (x2+1) = -(x-1)2 / (x2+1) < 0 et f(x) décroissante.
f(x) = ln [x2(1+1 /x2)] -x =ln(x2) +ln(1+1 /x2) -x =2 ln(x)+ln(1+1 /x2) -x.
f(x) = x[ 2 ln(x) / x +1 /x ln(1+1 /x2) -1]
En plus l'infini : ln(x) / x tend vers zéro par croissance comparée ; ln(1+1 /x2) tend vers zéro.
f(x) tend vers -1 /x soit moins l'infini.
Question 3 : En moins l'infini, la limite de exp(1-1 /x) est égale à :
A) 0 ; B) -oo ; C) e vrai.
En moins l'infini, -1 /x tend vers zéro.
Question 4 : L’équation différentielle y’=2y+3 a pour solutions les fonctions définies sur R par :
A) y(x) =C e2x.
B) y(x) =C e2x -1,5. Vrai
C) y(x) =C e2x +3. C est un réel.
Solution générale de y' -2y =0 : y(x) = C e2x.
Solution particulière de y’-2y =3.
y = -3 / 2
Solution générale de y’=2y+3 : y(x) =C e2x -1,5.
Question
5 : La dérivée de la fonction f définie par f(x) = ex /x est :
A) -ex / x2.
B) (x-1)ex / x2. Vrai.
C) xex / (x-1).
On pose u=ex et v = x ; u' = ex ; v' = 1.
(u'v-v'u) / v2 =(xex-ex) / x2.
Question 6 : L’écriture simplifiée de A= ln ( 3-5½) + ln ( 3+5½) est :
A) ln(4) vrai
B) ln(3) / 5½.
C) ln(6).
A = ln[(3-5½)(3+5½)] =ln(32-5)=ln(4).
Question 7 : 1 / e-2x est égal à :
A) e-2 *ex ; B) e2x vrai; C) ex /e2.
Question 8. Une primitive de la fonction f définie par f(x)=e3 x+1 sur R est :
A) e3x+1 / (3x) ;
B) e3x+1 / 3 vrai; C) 3e3x+1 .
Question 9 : La dérivée de la fonction f définie par f(x)=ln(3 x2+5) est :
A) 3x / (3 x2+5) ; B) (3 x2+5) ; C) 6x / (3 x2+5) vrai.
Question 10. Le nombre des effectifs d’un commissariat à la fin de l’année 2021+n est égal à
350-75×(2/3)n. À long terme, combien le commissariat comptera-t-il d’effectifs ?
A) 350 vrai; B) 700 ; C) 0.
(2/3)n tend vers zéro si n devient grand ; 75×(2/3)n va tendre vers zéro.
Exercice1 : (2,5 points)
Un sac opaque contient des munitions de différents calibres :
- Cinq munitions de calibre 7 mm
- Deux munitions de calibre 9 mm
- Une munition de calibre 11 mm
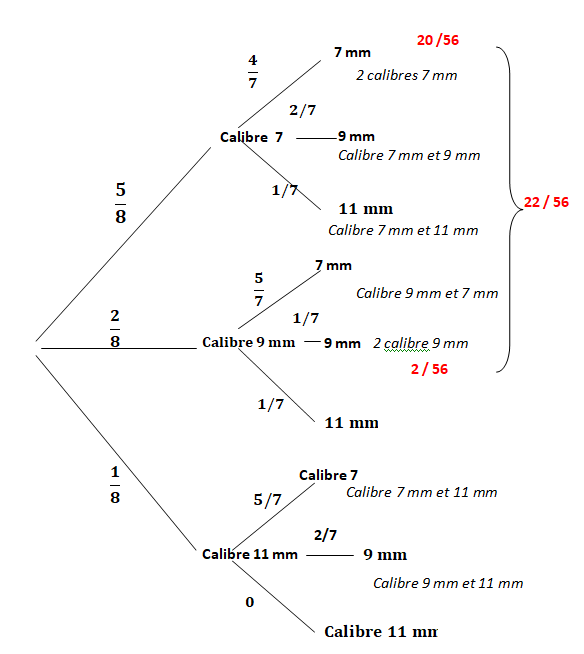
On extrait successivement et sans remise deux munitions.
On veut déterminer la probabilité d’extraire deux munitions de même calibre.
1. Représenter sur
un arbre tous les possibles en indiquant sur les branches
correspondantes la probabilité d’extraire deux munitions de chaque
tirage lors des deux tirages.
1. En déduire la probabilité d’avoir le couple (7mm, 7mm), (9mm, 9mm), (11mm, 11mm).
2. En déduire la probabilité d’extraire deux munitions de même calibre.