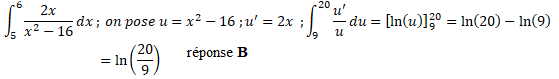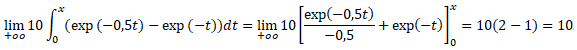Mathématiques.
Concours Ecole de Santé des Armées 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
1. ( 6 points)
QCM 1.
Un candidat doit répondre à un Vrai-Faux contenant 4 questions. Pour
chacune des questions, une réponse est vraie, l'autre est fausse. Le
candidat, n'ayant aucune connaissance sur les questions, choisit au
hasard entre les deux réponses possibles. Il a 1 point pour une réponse
exacte et 0 sinon.
La probabilité que le candidat obtienne au moins la moyenne à ce QCM est :
Notes possibles : 0 ; 1 ; 2 ; 3 ; 4.
Au moins la moyenne : 2 ; 3 ; 4.
Loi binomiale de paramètre n = 4 et p = 0,5.
P(X=2) + P(X = 3) +P(X=4) =0,6875 = 11 / 16. Réponse C.
QCM2
Pour traiter une maladie, on utilise deux médicaments :
• 80% des patients qui utilisent le premier médicament ont une réaction ;
• 30% des patients qui utilisent le deuxième médicament ont une réaction.
Les réactions aux deux médicaments sont indépendantes.
On note X la variable aléatoire correspondant au nombre de médicaments pour lesquels un patient a une réaction.
L'espérance mathématique de X vaut :
E(X) = 0,8 +0,3 = 1,1. Réponse C.
QCM3
Un virus sévit dans une population. On sait que dans cette population 20% des individus sont malades.
Un test diagnostique est mis en place. La probabilité qu'un individu
ait un test positif sachant qu'il est malade est 0,8 ; la probabilité
qu'un individu ait un test négatif sachant qu'il n'est pas malade est
0,8.
La probabilité qu'un individu ayant un test positif soit malade est :
On définit les événements suivants : M " la personne est malade" et T " le test est positif".
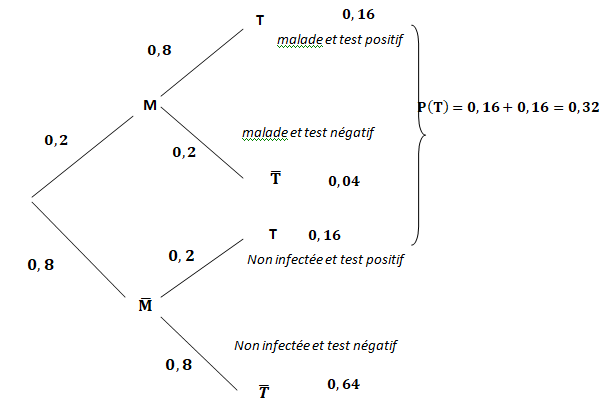
0,16 / 0,32 = 0,5 ; réponse A.
QCM4.
Soit une suite (un ) géométrique de raison 2 et une suite (vn ) géométrique de raison 3. Alors :
A. la suite sn = un + vn est arithmétique de raison 5. Faux
un =u0 x2n ; vn =v0 x3n ; un + vn diffère de sn=s0+5n.
B. la suite sn = un + vn est géométrique de raison 5. Faux.
C. la suite pn ·= un x vn est arithmétique de raison 6. Faux.
pn ·=u0 v0 x6n.
D. la suite Pn = un x Vn est géométrique de raison 6. Vrai.
QCM5
La limite de ln(x-2) / (2-x) quand x tend vers 2+ est :
On pose X = x-2 ; ln(X) / (-X) = -ln(X) / X.
En zéro, ln(X) tend vers -oo ; X tend vers zéro ; -ln(X) / X tend vers +oo.
Réponse C.
QCM6.
Dans R, l'équation ln(x + 3) + ln(x + 2) = ln(2):
A. n'admet pas de solution
B; admet une unique solution. Vrai
C. admet deux solutions
D. autre réponse.
Domaine de définition : ]-2 ; +oo[.
ln[(x+3)(x+2)] = ln(2) ; (x+3)(x+2) = 2 ; x2 +5x+4=0.
D = 52-4*4 =9 ; x1 = (-5+3) /2 =-1 ; x2 = (-5-3) /2 =-4.
Exercice 2 ( 6 points).
QCM7.
On considère la fonction f définie sur l'intervalle [-4 ; 4) par: f(x) = 1 + (x - 4)exp( 0,25x ).
Alors sur [-4 ; 4).
A. f est croissante
B. f est décroissante
C. f est convexe. Vrai.
D. f est concave.
Calcul de f '(x) en posant u = x-4 et v = exp(0,25x).
u' = 1 ; v' = 0,25 exp(0,25x) ; u'v+v'u = exp(0,25x)+0,25(x-4)exp(0,25x) =0,25 x exp(0,25x).
Sur [-4 ; 0 ], f '(x) < 0 et f(x) est décroissante ; Sur [0 ; 4 ], f '(x) > 0 et f(x) est croissante.
Calcul de f '(x) en posant u = 0,25x et v = exp(0,25x).
u' = 0,25 ; v' = 0,25 exp(0,25x) ; f ''(x) = 0,25 exp(0,25x) +0,252 x exp(0,25x)=0,25 exp(0,25x) ( 1+0,25x).
Sur [-4 ; +4 ], f "(x) est positive ou nulle : f(x) est convexe.
QCM8.
Soit la fonction f définie sur l'intervalle ] 4; +oo [par: f(x) =2x/(x2-16).
Alors l'intégrale suivante est égale à :
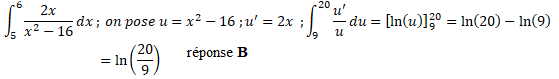
QCM9.
On considère· les droites d1 et d2 dont on donne une représentation paramétrique :
d1 : x= -3t + 1 ; y = -2t - 1; z = 6t + 4 avec t réel.
d2 : x = 2t'-2 ; y = -t'+3 ; z = 3t'-5 avec t ' réel.
Les droites d1 et d2 sont :
A. strictement parallèles
B. confondues
C. sécantes
D. non coplanaires.
Coordonnées d'un vecteur directeur de d1 : ( -3 ; -2 ; 6).
Coordonnées d'un vecteur directeur de d2 : ( 2 ; -1 ; 3).
Ces deux vecteurs ne sont pas colinéaires : les droites ne sont pas parallèles.
Hypothèse : elles sont sécantes et ont un point commun.
-3t+1 = 2t'-2 ; -3t = 2t'-3 ; t = -2/3 t'+1.
-2t-1 =-t'+3 ; -2t = -t'+4 ; t =0,5 t'-2, impossible. Les droites ne sont pas sécantes.
N'étant ni parallèles, ni sécantes, elles ne sont pas coplanaires. Réponse D.
QCM 10
Une tumeur, dont la surface triple chaque jour, met 12 jours pour
recouvrir totalement la surface S d'un certain organe. Combien de
jours, trois de ces tumeurs mettraient-elles pour recouvrir totalement
la surface de cet organe en supposant que les zones infectées par ces
trois tumeurs ne se recouvrent pas ?
Surface couverte par une tumeur en un jour : s ; en deux jours : 3s ; en trois jours : 9 s.
Suite géométrique de raison 3, de premier terme s.
Somme des termes : S = s(1-312) / (1-3) =s (312-1) / 2.
Surface couverte par trois tumeurs en un jour : 3s ; en deux jours : 9s ; en trois jours : 27 s.
Suite géométrique de raison 3, de premier terme 3s.
Somme des termes : S = 3s(1-3n) / (1-3) = 3s(3n-1) / 2.
312-1 =3(3n-1)=3n+1-3 ; 3n+1=312+2 ; (n+1)ln(3) =ln(312+2) ; n+1=12 ; n =11. Réponse A.
QCM 11.
Soit la fonctionfdéfinie sur R par: f(x) = x(x2+1)½. La dérivée f ' de la fonction f a pour expression :
On pose u = x et v = (x2+1)½ ; u'=1 ; v' =x(x2+1)-½ ; u'v+v'u = (x2+1)½ +x2 (x2+1)-½ ; réponse C.
QCM12.
Dans un pays, 80% des habitants ont une couverture vaccinale contre une maladie donnée.
On interroge au hasard 40 habitants et l'on considère que .la
population du pays est suffisamment importante pour assimiler cette
expérience aléatoire à un tirage aveè remise.
On pose X = nombre d'habitants vaccinés.
X suit la oi binomiale de paramère n = 40 et p = 0,8.
p(X=0)~ 0; p(X=40)~0 ; E(X) = 40 x0,8 = 32. Réponse C..
|
...
|
....
|
Exercice 3 .( 8 points).
A) On considère l'équation différentielle (E) : y' + y = 5 exp(-0,5t) sur l'intervalle [ 0; + oo [;
1) Démontrer que la fonction u définie sur [ 0; + oo [ par·: u(t) = 10 exp(-0,5t) est solution de (E).
u'(t) = -5exp(-0,5t) ; repport dans (E) :
-5exp(-0,5t)+10 exp(-0,5t)=5 exp(-0,5t) est vérifiée.
2) Résoudre l'équation différentielle (E0 ) : y' + y =0.
y = A exp(-t) avec A une constante.
3) En déduire toutes les solutions de (E).
y = A exp(-t) +10 exp(-0,5t).
4) Déterminer la fonction solution de (E) qui s'annule en O.
0= A exp(0) +10 exp(0) = A+10 ; A = -10.
y = -10 exp(-t) +10 exp(-0,5t).
B) Un
médicament est injecté par voie intramusculaire. Il passe dans le sang,
puis est éliminé par les reins. Une étude a permis de constater que la
concentration de ce médicament, en mmol. L-1, dans le sang à l'instant t, en heures, est donnée par :
f(t) = 10(exp(-0,5t)-exp(-t). L'injection a lieu à t=0.
1) Étudier les variations de la fonction f sur l'intervalle [ 0 ; + oo [.
f '(t) = 10 [ -0,5exp(-0,5t)+exp(-t)].
f '(t) = 0 si exp(-0,5t)=2 exp(-t) ; -0,5t = ln(2)-t ; t =2 ln(2)=ln(4) ~ 1,39.
Si x < 2 ln(2), f '(t) >0 et f(t) est croissante ; si x > 2 ln(2), f '(t) <0 et f(t) est décroissante.
2).Calculer la valeur de l'extremum de f.
f(ln(4)) = 10(exp(-0,5 ln(4))-exp(-ln(4)) = 10 (1/ exp(0,5 ln(4))-1/exp(ln(4))=10 (1/ 2-1/4)=2,5.
3) Déterminer la limite de f en +oo.
Quand t tend vers +oo, les termes en exponentielle tendent vers zéro et f(t) tend vers zéro.
4) Dresser le tableau de variation complet de la fonction f sur] 0 ; + oo [.
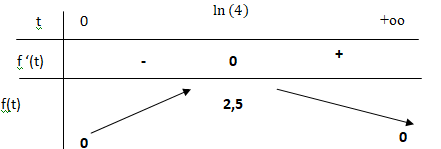
5) Soit C la courbe représentative de la fonction f.
a) Déterminer l'équation de la tangente à C au point d'abscisse O.
y = f '(0) t = 5 t.
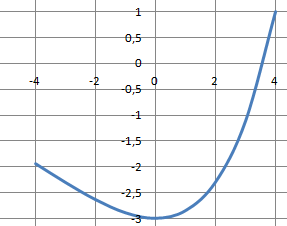
b) Tracer une allure de C dans un repère orthonormé.
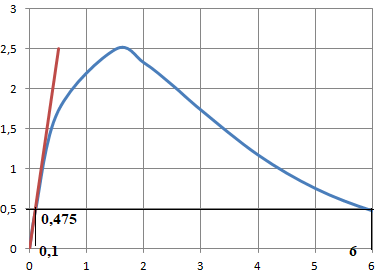
6) On estime que le médicament est éliminé dès que· sa concentration dans le sang redevient inférieure à 0,475 mmol. L-1.
a) Justifier que l'équation f(t)=0,475 admet deux solutions dans l'intervalle] 0; + oo [ .
f(0) = 0 et f(ln(4) = 2,5 ; de plus la fonction est croissante sur [0 ; ln(4)].
La fonction tend vers zéro si t tend vers +oo et f(ln(4) = 2,5.
De plus la fonction est décroissante sur [ ln(4) ; +oo[.
D'après le théorème des valeurs intermédiaires ( ou d'après le tableau
de variations ) l'équation f(t)=0,475 admet deux solutions dans
l'intervalle] 0; + oo [
b) Résoudre l'équation : f(t)=0,475 dans] 0; + oo [.
10(exp(-0,5t)-exp(-t) = 0,475 ;
exp(-0,5t)-exp(-t) = 0,0475.
exp(-0,5t)-exp(-0,5t-0,5t) = 0,0475.
exp(-0,5t)-exp(-0,5t) x exp(-0,5t) = 0,0475.
On pose X = exp(-0,5t) >0.
X2-X+0,0475 = 0.
D = (-1)2 -4 x0,0475 =0,81 = 0,92.
X1 = (1-0,9) / 2 = 0,05 ; X2 = (1+0,9) / 2 = 0,95.
-0,5t1 =ln(0,05) ; t1 ~ 6 h.
-0,5t2 =ln(0,95) ; t2 ~ 0,1 h.
c) En déduire l'instant à partir duquel le médicament est éliminé.
Le médicament est éliminé au bout de 6 heures..
7) En pharmaceutique, on appelle ASC d'une concentration, en ·mmol. L-1, le nombre suivant :
a) Calculer l'ASC de cette concentration.
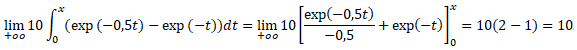
b) Interpréter graphiquement la valeur obtenue.
Aire comprise entre la courbe C et l'axe des abscisses.
8) a) Montrer que la courbe représentative C de la fonction f présente un point d'inflexion en un réel x0 de [ 0; + oo [ que l'on précisera.
b) En donner une interprétation pour la courbe C et pour la concentration.
f '(t) = 10 [ -0,5exp(-0,5t)+exp(-t)].
f "(t) = 10 [0,25 exp(-0,5t)-exp(-t)].
f "(t) s'annule et change de signe pour 0,25 exp(-0,5t)=exp(-t).
ln(0,25 exp(-0,5t) = -t ; ln(0,25) -0,5t = -t ; ln(4) = 0,5 t ; t = 2 ln(4) = 4 ln(2).
En ce point la concavité de la courbe change.
La vitesse de disparition du médicament commence à décroître à partir de ce point.
|
|