Top
Gun, différentes phases du vol d'un avion,
Concours EMIA 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Partie A. Vol en montée.
Absence de vent. l'axe vertical est orienté vers le haut.
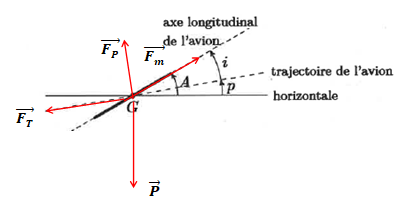
p : pente, angle de l'horizontale vers la trajectoire de l'avion.
A : assiette, angle de l'horizontale vers l'axe longitudinal de l'avion.
i : incidence, angle de la trajectoire vers l'axe longitudinal.
On s'intéresse au mouvement du centre d'inertie G de l'avion, de masse m = 2,3 103 kg et soumis aux forces suivantes :
son poids P, la force motrice Fm des réacteurs dont la direction est l'axe longitudinal,
la portance FP = 0,5 r Sv2Cp perpendiculaire à la trajectoire de l'avion
la traînée de même direction que la trajectoire mais de sens opposé, de norme FT = 0,5 r Sv2Ct.
r = 1,2 kg m-3, masse volumique de l'air supposé incompressible ;
S = 220 m2, surface caractéristique de l'avion :
v : vitesse de l'avion par rapport à l'air.
Cp = 0,24 ; Ct = 0,008.
1- Représenter les forces. Quelle force maintient l'avion en l'air ?
P = m g =2,3 103 x9,8 ~2,3 104 N.
La portance maintient l'avion en l'air.
On suppose : i = 0 donc ( A = p) ; une pente p= 10° et une montée d'un mouvement rectiligne uniforme.
2. Préciser ce qu'est un mouvement rectiligne uniforme. Que vaut l'accélération dans ce cas ?
Dans un mouvement rectiligne uniforme, le vecteur vitesse est constant et le vecteur accélération est nul.
3. Ecrire la seconde loi de Newton et la projeter dans la direction de la trajectoire et la direction orthogonale.
Selon la trajectoire : -FT -mg sin (A) + Fm =0.
Selon la normale à la trajectoire : FP -mg cos (A) = 0.
4. En déduire que v = [2mg cos A / (rSCp)]½. Calculer v.
-0,5 r Sv2Cp -mg cos (A) = 0.
r Sv2Cp =2mg cos (A) ; v = [2mg cos A / (rSCp)]½.
v=[2 x2,3 10 3 x9,8 cos(10) / (1,2 x220x0,24)] ½=26,5 m /s.
Vol en virage.
On suppose que le virage suit un arc de cercle de rayon R = 200 m à la vitesse constante v = 60 m /s.
1. Donner la formule de l'accélération pour un mouvement circulaire uniforme et faire l'application numérique.
a N = v 2 / R =60 2/200=18 m s -2.
2. Comment appelle t-on la force à laquelle le pilote est soumis ?
Force d'inertie centrifuge.
Partie B. Le mur du son.
1. Rappeler la valeur approximative de la vitesse du son dans l'air.
c =340 m /s.
2. Un avion se déplace à mach 2. Quelle est la relation simple entre la vitesse du son et celle de l'avion notée v ?
v = 2 c.
3.
Donner l'expression de la distance da parcourue par l'avion durant le
temps T. En déduire l'expression de la distance parcourue parcourue par
le son d s en fonction de d a.
d a = v T ; d s = c T ; da = 2 ds.
On fait le schéma suivant pour représenter la situation. La position de l'avion est représentée aux instants t et t+T.
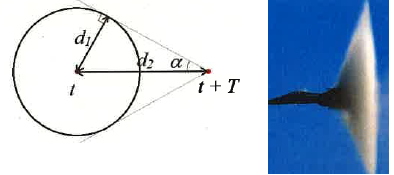
4. Identifier d1 et d2 : laquelle est ds, laquelle est da ?
d2 : distance parcourue par l'avion pendant la durée T ; d1 distance parcourue par le son durant la même durée T.
5. En déduire la valeur de l'angle a.
sin a = d1 / d2 = 0,5 ; a ~30°.
On souhaite généraliser cette relation à un avion se déplaçant à une vitesse v quelconque.
6. Montrer que sin a = c / v.
La figure
ci-dessous décrit quant à elle les ondes émises par un avion ayant une
vitesse v > vson. Les surfaces d’ondes s’alignent alors
suivant un cône.
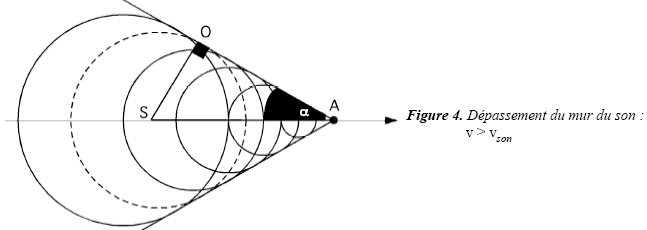
- Pendant le temps t, l’avion parcourt la distance SA. En déduire une
relation entre SA, v et t. Pendant ce même temps t, l’onde partie de S
- en pointillés dans la figure ci-dessus - parcourt la distance SO.
sin a = SO/SA = vson / v.
7. En déduire la vitesse de l'avion de la photo.
a est de l'ordre de 70 ° ; v = c / sin 70 = 340 / 0,94 ~360 m /s.
8. Expliquer en quoi est due la déflagration que l'on entend lorsqu'un avion passe le mur du son.
Lorsqu’il
accroît sa vitesse et qu’il atteint la célérité du son, les ondes de
pression s’accumulent devant le nez de l’avion. Lorsqu’il dépasse la
célérité du son (on dit qu’il passe le mur du son), il se produit alors
des ondes de compression et de dilatation qui provoquent ce fameux «
bang ».
|
...
|
....
|
De l'orage dans l'air.
un
orage est le résultat d'accumulation de charges à la base d'un nuage,
dû aux frottements entre différentes couches d'air. Quand la charge
accumulée devient trop forte, une décharge électrique apparaît avec la
surface de la terre chargée à l'opposé.
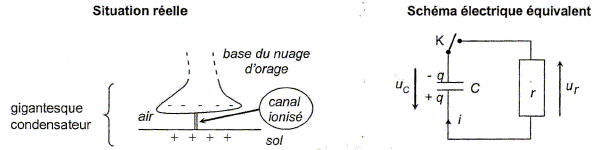
1. L'air est-il normalement conducteur ?
L'air constitué de molécules de diazote et de dioxygène n'est pas normalement conducteur.
2. Justifier le modèle de " gigantesque condensateur" de la figure.
Par temps d'orage, on peut comparer le
système {base du nuage - sol} à un
gigantesque condensateur constitué par l'air
placé entre le bas du nuage et le
sol.
L'isolant entre les deux armatures est
l'air ; dans certaines conditions, il devient
localement conducteur. Il s'établit alors un
canal ionisé entre le sol et le nuage dans
lequel une ou plusieurs décharges se
produisent. Ces décharges constituent la
foudre.
On donne la valeur de la tension de claquage de l'air rendant possible le passage du courant : 3600 kV / m.
3. Sachant que la base du nuage se trouve à l'altitude h = 1,5 km, calculer la tension uc 0 aux bornes du condensateur juste avant l'éclair.
uc 0 = 3600 x1,5 103 =5,4 106 kV.
4. Montrer que la tension uc(t) aux bornes du condensateur obéit à l'équation différentielle suivante après fermeture de l'interrupteur K.
Loi des mailles : ur+uc(t) = 0 ; ur = r i ; i = dq /dt = Cduc(t) / dt.
r Cduc(t) / dt+uc(t) = 0.
On pose t = r C ; duc(t) / dt+uc(t) / t = 0.
5. Résoudre cette équation et dessiner l'allure de la courbe.
uc(t) = A exp(-t / t) avec A une constante.
uc(0) = A =uc 0 ; uc(t) = uc 0 exp(-t / t).
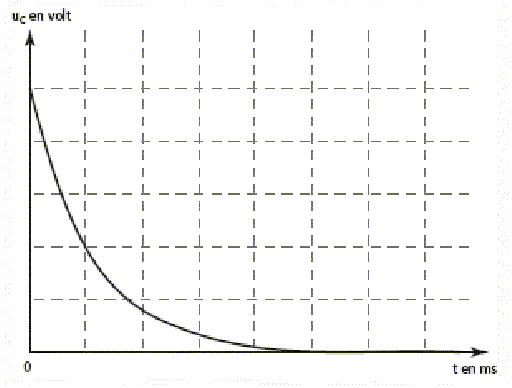
6. On donne t = 30 ms. Quelle est la durée totale de la décharge à 99 % ? Commenter.
uc(t) = uc 0 exp(-t / t) ; 0,99 uc 0 = uc 0 exp(-t / 30).
0,99 = exp(-t / 30) ; ln(0,99) = -t / 30 ; t ~ 0,3 ms.
Cette valeur est très inférieure à la durée d'observation de l'éclair.
7. Expliquer pourquoi le pilote est en sécurité même si un éclair frappe l'appareil.
La carlingue métallique de l'avion fait office de cage de Faraday.
L'éclair se déplace à la surface de l'avion sans pénétrer à l'intérieur.
Quand la charge électrique s'accumule à l'extérieur d'une boîte
métallique, les électrons dans le métal se déplacent pour annuler toute
charge se trouvant à l'intérieur.
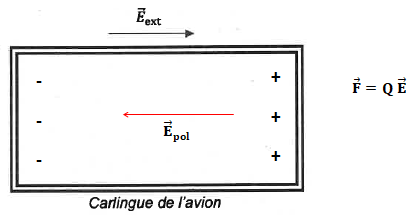
8. Donner
l'expression de la force de Lorentz exercée par un champ
électrique E sur une charge q. Reproduire le schéma ci-dessous en
représentant les charges positives et négatives qui apparaissent sur la
carlingue à cause du champ extérieur. Indiquer également la direction
du champ de polarisation Epol créé par ce déplacement de charges.
9. Montrer à l'aide
du théorème de Gauss que si le champ émectrique E est nul dans un
certain volume V, alors la charge Q contenue à l'intérieur de ce volume
est nécessairement nulle.
Soit un point M situé à
l'intérieur de la sphère, à une
distance OM=x du centre.
Par raison de symétrie le champ est radial.
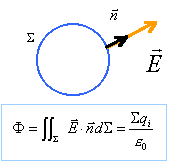
On considère une sphère
S , de centre O et de
rayon x.
D'après le théorème de Gauss, le
flux du vecteur champ électrique à travers la
surface S est nul car
il n'y a pas de charge à l'intérieur de
S.
si x < R, le champ électrique est nul à
l'intérieur de la sphère.
Arme nucléaire .
1. Définir ce qu'est une réaction de fission nucléaire.
Dans une réaction de fission nucléaire, un noyau lourd " fissile" donne
naissance à deux noyaux plus légers. La réaction se fait avec perte de
masse et dégagement d'énergie.
2. Sous l'action d'un neutron un noyau de plutonium 239 23994Pu peut fissionner en libérant plusieurs neutrons et deux noyaux fils. Si la fission produit 3 neutrons et un noyau de Tellure 13552Te, quelle est la composition du second noyau fils ?
23994Pu +10n --> 13552Te + 310n +AZX.
Conservation de la charge : 94 = 52 +Z ; Z =42 ( molybdène Mo).
Conservation du nombre de nucléons: 239+1 = 135+3+A ; A = 102.
3. Calculer la perte de masse Dm.
Dm = m(13552Te) + 2(10n) +m(AZX) -m(23994Pu) =134,91645+2*1,00866+101,910297-239,05216=-0,208093 u.
1 u = 1,66054 10-27 kg ; Dm =-0,208093 x 1,66054 10-27 =-3,455 10-28 kg.
4. Déterminer l'expression puis l'énergie dégagée par la fission d'un seul noyau de plutonium 239.
E = |Dm|c2 =3,455 10-28 x(3 108)2 =3,1 10-11 J.
5..Connaissant l'énergie dégaggée par une bombe nucléaire (8,78 1013 J), calculer le nombre de noyau de plutonium 239 ayant réagi.
8,78 1013 / (3,1 10-11 ) =2,8 1024.
6. En déduire le rendement = nombre de noyaux ayant réagi / nombre initial de noyaux.
Initialement 6,4 kg de plutonium . M(Pu) =239 g / mol.
6,4 103 / 239 =26,78 moles.
Nombre de noyaux initiaux : 26,78 *NA = 26,78 *6,02 1023 =1,61 1025 noyaux.
Rendement : 2,8 1024 / (1,61 1025)=0,17 ( 17 %).
La montre à quartz du pilote.
On donne la courbe de réponse en tension d'un quartz soumis à différentes fréquences d'excitation.
1. Donner la fréquence de résonance du quartz.
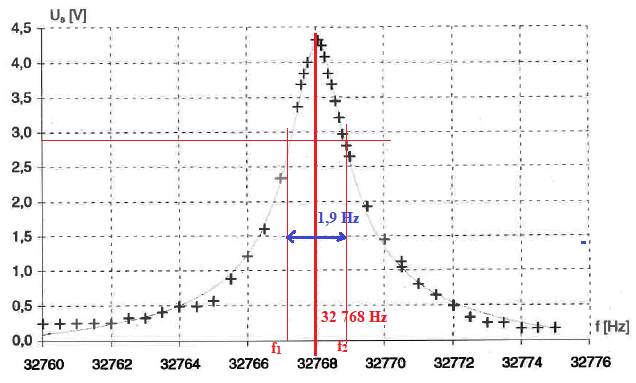
On pose f1 et f2 les fréquences correspondant à l'amplitude maximale divisée par 2½.
2. Exprimer le facteur de qualité Q..
Q = fréquence de résonance / bande passante = fr / |f2-f1|
3. Déterminer graphiquement f1 et f2 puis calculer Q. Conclure.
4,3 / 2½ ~2,86 V.
Q = 32768 / 1,9 ~ 3,4 104.
Q est très grand, l'oscillateur est très sélectif.
La fréquence de résonance de ce cristal de quartz dépend de la
température. La montre est réglée pour fonctionner correctement à T0=25°C. On modélise l'écart de fréquence par rapport à cette fréquence de référence f0 par :
Df / f0 = A(T-T0) + B(T-T0) 2+ C(T-T0) 3.
Le quartz étudié présente une fréquence de résonance f0 = 32 764,4 Hz à 25°C et f1 = 32 764,0 Hz à T1 = 50°C.
4. Déterminer l'angle de coupe du quartz à l'aide de la figure.
Df / f0 =(f1-f0) / f0 = -0,4 / 32 764 x 106 ~ -12 ppm.
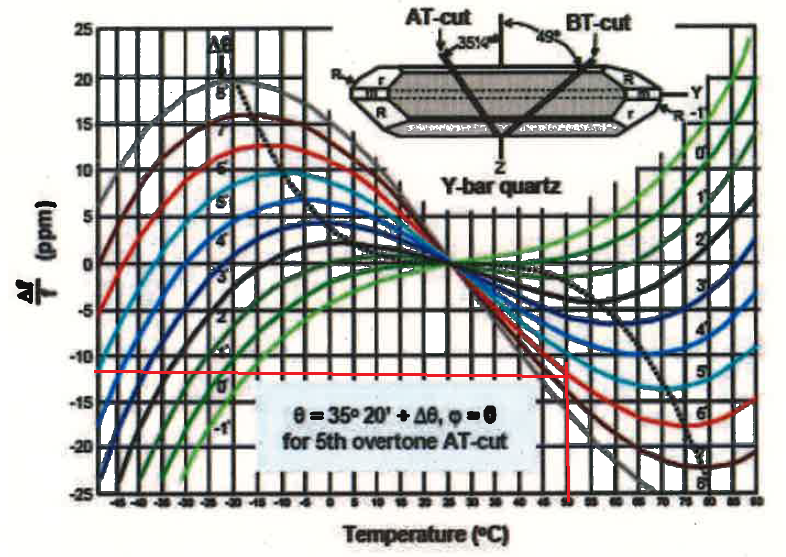
La courbe la plus proche est la courbe rouge. Dq ~ 6 minutes d'arc.
Angle de coupe : q = 35° 20' +6 = 35° 26'.
5. Calculer la valeur du coefficient A si B et C sont négligeables quand |T-T0| < 50°C.
Df / f0 = A(T-T0) ; A = -12 / 25~ -0,5 ppm °C-1.
6. Déterminer en secondes le décalage entre l'heure vraie et l'heure indiquée par la montre, au bout d'une journée à 50°C.
La fréquence de résonance diminue si la température s'élève. La période, inverse de la fréquence, croît. La montre retarde.
Df / f0 = -12 ppm.
1 jour = 24 x3600 =86400 s ; retard :12 10-6 x 86400 ~1 s.
|
|