Mathématiques,
Concours EMIA 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. Nombres complexes..
1- Ecrire le complex w = (1+i) / (2-3i) sous forme algébrique..
w = (1+i) ( 2+3i) / (4+9)=((2+3i2) +i(2+3)) / 13= (-1+5i) / 13.
2. Résoudre l'équation suivante :
On pose : z = x +iy avec x et y réels.
x+iy-i = 3(x-iy) -1.
x+i(y-1) = 3x-1-3iy ;
Egalité des parties réelles : x = 3x-1 soit x = 0,5.
Egalité des parties imaginaires : y-1 = -3y soit y = 0,25.
z = 0,5 +0,25 i.
3. On considère les nombres complexes a = 1+i et b = 3½-i.
a. Ecrire ces
nombres sous forme exponentielle. En déduire l'écriture de ab sous
forme exponentielle et en déduire les valeurs de cos (p/12) et sin(p/12).
Module de a : |a| = (12+12)½ = 2½.
a / |a| =1 /2½ + i / 2½= cos(p/4) + i sin (p/4) ; a =2½ exp(ip/4).
Module de b : |b| = (3+12)½ = 2.
b / |b| =3½ / 2-0,5 i = cos(-p/6) + i sin (-p/6) ; b =2 exp(-ip/6).
ab =2 * 2½ exp(ip/4-ip/6 ) =2 * 2½ exp(ip/12) = 2 * 2½ cos (p/12) + 2 * 2½ i sin (p/12).
ab = (1+i)( 3½-i) = 3½+1 +i(3½-1).
cos (p/12) =(3½+1) / (2 * 2½) ; sin (p/12) =(3½-1) / (2 * 2½).
Exercice 2. calculs algébriques.
1. Ecrire les quantités suivantes sans valeuurs absolues.
A(x) = |-x+2|.
Si x < 2, A(x) = -x+2.
Si x > 2, A(x) = x-2.
B(x) = |3x2-x-2|.
Solutions de 3x2-x-2 = 0 : D =1+24=25 = 52.
x1 = (1+5) / 6 = 1 et x2 = (1-5) / 6 = -2/3.
Si x appartient à [-2 /3 ; 1], B(x) =-3x2+x+2.
Si x appartient à ]-oo ;-2 /3 ] union [1 ; +oo[ , B(x) = 3x2-x-2.
2. Donner les solutions des équations suivantes :
(E1) (2x-3)2 = (7x+5)2.
4x2+9-12x =49x2+25+70x.
45x2+82x+16=0 ; D =822 -4*16*45= -3884 = 3884 =622.
x1 = (-82-62) / 90= -1,6 ; x1 = (-82+62) / 90= -2 / 9.
ou bien : 2x-3 = 7x+5 et 2x-3 = -7x-5 soit x = -1,6 et x = -2 /9.
(E2) : |-2x2+2x+1| = 3.
Solutions de -2x2+2x+1=0 ; D = 4+8=12 = (2*3½)2.
x1 = (-2+2*3½) / (-4) = (1-3½) / 2 ~-0,37 ; x2 = (-2-2*3½) / (-4) = (1+3½) / 2 ~1,36.
Si x appartient à [-0,37 ; 1,36] : |-2x2+2x+1| = -2x2+2x+1 = 3 ; -2x2+2x-2 = 0 ; x2-x+1 = 0.
Discriminant : D = 1-4=-3 =3i2= (3½i)2.
x1 = (1+3½i) / 2 et x2 = (1-3½i) / 2. .
Sinon : -2x2+2x+1 étant négatif : 2x2-2x-1 = 3 ; 2x2-2x-4 =0 ; x2-x-2 =0
Discriminant : D = 1+8=9 = 32.
x1 = (1+3) / 2 = 2 et x2 = (1-3) / 2 =-1.
3. Résoudre les inéquations suivantes :
|-4x+3| < 1 avec x réel.
Si x < 3 / 4 : -4x+3 < 1 ; -4x < -2 ; x appartient à ]0,5 ; 3/4[.
Sinon : -3+4x < 1 ; 4x < 4 ; x appartient à ]3 /4 ; 1[.
(x+1) / (x-2) < (x+2) / (x+3) avec x différent de 2 et -3.
(x+1)(x+3) < (x+2)(x-2) ; x2+4x+3 < x2-4 ; 4x+3 < -4 ; 4x < -7 ; x < -7 /4 et x différent de -3.
Exercice 3. Géométrie.
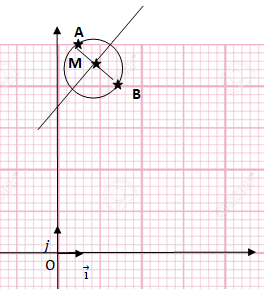
A(1 ; 10) ; b(3 ; 8).
1. Déterminer les équations cartésiennes du cercle de diamètre [AB] et de la médiatrice du segment [AB].
Coordonnées du centre du cercle : (xA+xB) / 2 = 2 ; (yA+yB) / 2 = 9.
AB = [(3-1)2+(8-10)2]½= 8½=2 x2½.
Rayon du cercle : R =AB / 2 = 2½.
Equation du cercle : ( x-2)2+(y-9)2 = R2 =2..
La médiatrice du segment [AB] est perpendiculaire au segment en son milieu M (2 ; 9).
Coefficient directeur de la droite (AB) : (yB-yA) / (xB-xA) = -2 / 2=-1.
Coefficient directeur de lamédiatrice : 1.
Equation de la médiatrice : y = x +b.
M appartient à la médiatrice : 9 = 2 +b ; b = 7. y = x+7.
2. A(1 ; 0 ; 1) ; B(1 ; 1 ; 1) ; C(0 ; 1 ; 2).
a. Justifier que ces points ne sont pas alignés.
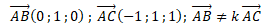
Ces vecteurs n'étant pas colinéaires, ces points ne sont pas alignés.
b. Donner une équation cartésienne du plan (ABC).
ax +by +cz +d = 0.
A appartient à ce plan : a+c+d =0. (1).
B appartient à ce plan : a+b+c+d =0. (2).
C appartient à ce plan : b+2c+d =0. (3).
(2)-(1) donne : b=0.
(3) devient : 2c+d =0 ; d = -2c.
(1) devient : a=c= -½d..
ax +az -2a = 0 ; x+z-2=0.
c. Les points D(1 ; 2 ; 3) et E(2 ; 1 , 0) appartiennent-ils au plan (ABC) ?
Si D appartient à ce plan : xD +zD-2 =0 ; 1+3-2=2 différent de zéro. D n'appartient pas à ce plan.
Si E appartient à ce plan : xE +zE-2 =0 ; 2+0-2=0 . E appartient à ce plan.
.
Exercice 4- Dérivées, primitives..
1. Calculer les dérivées des fonctions suivantes sur ]0 ; +oo[.
f(x) = ln(3x) + ln(x3) ; f '(x) = 1 / x +3x2 / x3 =1 /x+3/x=4 /x.
f(x) = (ln(x))2 ;on pose u = ln(x) ; u' = 1/x ; (u2)' ) 2uu' ; f ' (x) = 2 ln(x) / x.
f(x) =exp(2x2-1) ; on pose u = 2x2-1 ; u' = 4x ; f '(u) = u' exp(u) ; f '(x) = 4x exp(2x2-1).
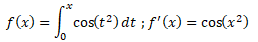
2. Calculer les intégrales suivantes :
 . .
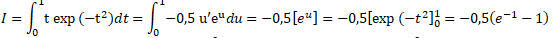
On pose u = -t2 ; u' = -2t.
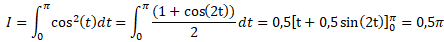
3.a Soit k entier naturel non nul. Calculer :
 b.
b. Soit n un entier naturel supérieur ou égal à 2. Montrer que :
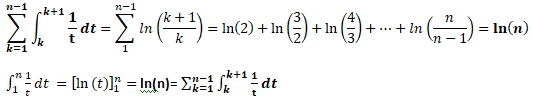
c. Déduire de ce qui précède une simplification de la somme suivante pour n > 2.
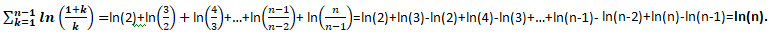
d. Déterminer si elle existe la limite de cette somme.
Quand n tend vers l'infini, ln(n) tend vers plus l'infini.
Exercice 5. Probabilités.
1.
Une urne contient 6 boules blanches et 4 boules rouges. On extrait
trois fois une boule de l'urne avec remise et on note X la varible
aléatoire indiquant le nombre de boules blanches obtenues.
a. Quelle est la loi de probabilité de X.
Loi binomiale : les tirages sont identiques et indépendants et il y a deux issues possibles.
Paramètres : nombre de boules n = 10 ; probabilité de tirer une boule blanche p =6/10 =0,6.
2. Quelle est la probabilité d'obtenir 3 boules blanches ?
p(X=3 ) = (10 3) 0,63 (1-0,6)10-3 =10*9*8 / (2*3)*0,63 *0,47 =0,0425.
c. Quelle est l'espérance de X ?
np = 10 x0,6 = 6.
d. Quele est la variance de X ?
npq = 10 x0,6 x0,4=2,4.
2. On considère un
dé à 6 faces numérotées de 1 à 6. Ce dé est truqué de façon à ce que la
probabilité d'obtenir un numéro soit proportionnelle à ce numéro..
Autrement dit , il existe un réel l >0 tel que :
quelque soit k appartenant à [1 ; 6], P(X=k) = l k.
a. Déterminer la valeur de l.
l +2l +3l+4l+5l+6l = 1 ; l = 1/ 21.
b. Quelle est la probabilité d'obtenir un numéro pair ?
P(X=2) + P(X=4) + P(X=6)=2l +4l +6l =12 / 21.
c. Déterminer l'espérance de X.
k
|
1
|
2
|
3
|
4
|
5
|
6
|
P(X=k)
|
1 /21
|
2 /21
|
3 /21
|
4 /21
|
5/21
|
6/21
|
E(X) = [1/21 +2*2/21 +3*3/21+4*4/21+5x5/21+6*6/21=13 /3.
|
...
|
....
|
Exercice 6 : Suites.
La suite (un) est définie par u0 = 1,5 et un+1 = (un-1)2+1 pour tout n > 0.
1. Etudier les variations de la fonction f(x) =(x-1)2+1 sur ]1 ; 2[.
f '(x) = 2(x-1) > 0 sur ]1 ; 2[.
f(x) est strictement croissante de 1 à 2 sur cet intervalle.
2. Montrer que pour tout n entier, 1 < un < 2.
un+1 =f(un) ; f(un) appartient à ]1 ; 2[ ; donc 1 < un < 2.
3. Etudier la monotonie de la suite et en déduire qu'elle converge.
f(un) est strictement croissante ( donc monotone) sur ]1 ; 2[.
f(un) appartient à ]1 ; 2[.
un+1 =f(un) : la suite est donc croissante et bornée par 2 : donc elle converge.
4. Déterminer la limite de cette suite.
A la limite l : l = (l -1)2+1.
l2-3l +2= 0 ; D =9-8=1 ; l =(3+1) / 2 = 2.
Exercice 7 . Fonction.
f(x) = ln(1-x2) -ln(3x)+ln(2)
1. Préciser le domaine de définition I.
f(x) = ln(2((1-x2)/(3x)).
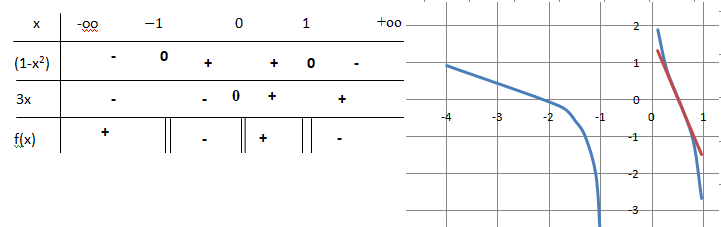
I est ]-oo ; -1[ union ]0 ; 1[.
2. Déterminer les limites de f aux extrémités de I.
((1-x2)/(3x)= (1/x-x) / 3.
En -oo : 1/x tend vers zéro et f(x) tend vers +oo.
En -1-: (1/x-x) / 3 tend vers zéro et f(x) tend vers -oo.
En 0+ : (1/x-x) / 3 tend vers +oo et f(x) tend vers +oo.
En 1-: (1/x-x) / 3 tend vers zéro et f(x) tend vers -oo.
3. Justifier que f est dérivable et déterminer l'expression de sa dérivée.
f(x) est la somme ou la différence de fonctions dérivables : donc f est dérivable.
f '(x) = -2x /(1-x2) -1 /x = - [2x2+1-x2] / [(1-x2) x] = [x2+1] / [(x2-1) x].
4. Déterminer les variation de f sur I.
Le signe de la dérivée est celui de (x2-1) x :
sur ]-oo ; -1[ : (x2-1) x < 0 et f(x) est strictement décroissante.
sur ]0 ; 1[ : (x2-1) x < 0 et f(x) est strictement décroissante.
5..Déterminer une équation de la tangente à la courbe en x = 0,5.
y = a x+b avec a = f '(0,5) = [0,52+1] / [(0,52-1) *0,5]= -10 /3.
Le point de coordonnées (0,5 ; f(0,5) appartient à la tangente :
f(0,5) = ln(2((1-0,52)/(3*0,5)=ln(1)=0
0=-10/3 *0,5 +b ; b = 5 /3 ; y = -10 x /3 +5/3.
Exercice 8. Polynômes.
P(x) = x3+x+1= (x-a)(x-b)(x-c)
1. Montrer que ab+ac+bc=1.
(x-a)(x-b)= x2-(a+b)x+ab.
(x2-(a+b)x+ab)(x-c)=x3-(a+b+c)x2+(ac+bc+ab)x -abc.
On identifie : ab+ac+bc=1.
2. Calculer a+b+c.
On identifie : a+b+c=0.
3. En développant (a+b+c)2, en déduire que a2+b2+c2=-2.
(a+b+c)2= a2 +b2 +c2 +2ac+2bc+2ab= a2 +b2 +c2 +2=0..
4. Effectuer la division enclidienne de x4 par P.
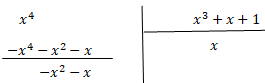
x4=x (x3+x+1) -x2-x.
5. Déduire des questions précédentes la valeur de a4+b4+c4.
(a2+b2+c2)2=a4+b4+c4+2(a2b2+b2c2+a2c2)=4.
(ab+ac+bc)2 =a2b2+b2c2+a2c2+2(a2bc+b2ac+c2ab)=1.
Or a2bc+b2ac+c2ab= abc(a+b+c)=0.
a4+b4+c4= 4-2(a2b2+b2c2+a2c2)=4-2=2.
Exercice 9. Matrices.
1. Calculer le produit PQ. En déduire que la matrice P est inversible et déterminer son inverse.
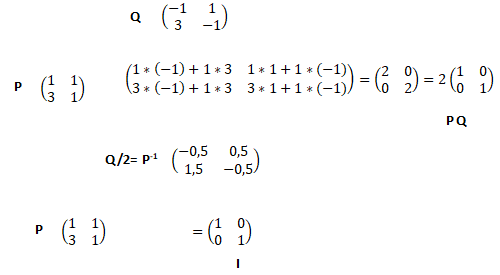
2. Calculer D = P-1AP.

3. Montrer que ND = DN si et seulement si b = c = 0.
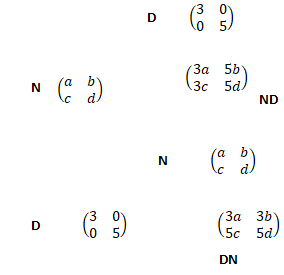
4. Soit la matrice N telle que N2=D. Montrer que ND = DN.
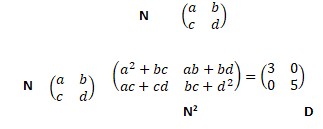
On identifie ab+bd=0 ; b(a+d)=0 soit b=0 ou bien a = - d.
a2+bc = 3 et bc +d2 = 5 ; donc a = -d n'est pas à retenir.
ac+cd=0 ; c(a+d)=0 soit c=0.
5. Déduire des questions précédentes toutes les matrices N telles que N2 = D.
b = c = 0 ; a2= 3 ; d2 = 5.
6. En déduire un moyen d'obtenir toutes les matrices M telles que M2 = A.
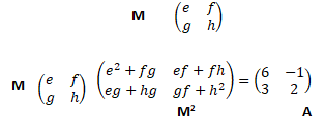
On identifie :e2+fg = 6 ; ef+gh = -1 ; eg+hg=3 ; gf+h2 = 2.
|
|