Les intégrales de Wallis,
Concours CAPLP maths sciences 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
On considère la suite d’intégrales ((Sn) définie pour tout entier naturel n par
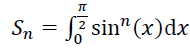
12. Les premiers termes.
a. Calculer S0 et S1.
S0 =[x]0 p/2=p/2.
S1 =[-cos(x)]0 p/2=1.
b. Soit x réel. Exprimer sin2(x) en fonction de cos(2x) et en déduire la valeur de S2.
sin2(x)=(1-cos(2x) / 2.
S2 =0,5[x-0,5sin(2x)]0 p/2=0,5 x p/2= p/4.
c. Après avoir justifié que, pour tout réel x, on a sin3(x)=sin(x)−sin(x) cos2(x), calculer la valeur de S3.
sin3(x)= sin(x) sin2(x)= sin(x) [1-cos2(x)] =sin(x)−sin(x) cos2(x).
Primitive de sin(x) cos2(x) : on pose u = cos(x) ; u' = -sin(x).
−sin(x) cos2(x)= u'u2. Primitive de u'u2= u3/3=cos3(x) / 3.
S3=[-cos(x)+cos3(x) / 3]0 p/2= 1-1/3 =2/3.
13. Sens de variation de la suite.
a. Justifier que pour tout nombre réel x appartenant à l’intervalle [0 ; p/2] et tout entier naturel n, on a : 0 < sinn+1(x) < sinn(x).
0 < x < p/2 entraîne 0 < sin(x) < 1 entraîne 0 < sinn+1(x) < sinn(x)
. b. En déduire que la suite (Sn) est convergente.
D'après les propriétés de l'intégrale d'une fonction continue :

La suite est à termes positifs, décroissante et minorée par 0 : donc elle converge.
14. Limite de la suite.
a. Démontrer, à l’aide d’une intégration par parties, que pour tout entier naturel n, Sn+2=(n+1) / (n+2)Sn.
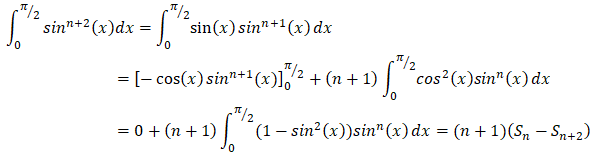
Sn+2=(n+1)(Sn-Sn+2)=(n+1) Sn-(n+1)Sn+2.
(n+2)Sn+2 =(n+1) Sn.
b. Montrer que la suite (Rn) définie par Rn=(n+1)SnSn+1 est constante et donner la valeur de cette constante.
Rn+1=(n+2)Sn+1Sn+2 =(n+2)Sn+1 (n+1) / (n+2)Sn=(n+1)Sn Sn+1 =Rn=constante.
Valeur de la constante : R0 = (0+1)S0 S1 =p/2.
c. En déduire que (Sn) a pour limite 0.
(n+1)SnSn+1 =p/2.
0 < Sn+2 < Sn+1 < Sn.
Sn+2 / Sn =(n+1) / (n+2) < Sn+1 / Sn < 1.
donc Sn+1 ~ Sn ; Sn2 ~ p /(2n) ; Sn tend vers zéro si n devient très grand.
15. Application aux calculs des termes.
a. À l’aide de la relation de récurrence trouvée précédemment, retrouver la valeur de S3 déjà obtenue à la question 12.
(n+1)SnSn+1 =p/2.
(2 +1)S2 S3 = p/2.
3 p/4 S3 = p/2.
S3 =2 / 3.
b. Donner l’expression générale de Sn selon la parité de n.
(n+2)Sn+2 =(n+1) Sn. En posant 2p =n+2 :
S2p=(2p-1) / (2p) S2p-2 .
S2p-2= (2p-3) / (2p-2) S2p-4 .
S2p=(2p-1) (2p-3) S2p-4 / [2p (2p-2)] = ... =(2p-1) (2p-3)....x1 / [2p (2p-2)x ... x 2] S0.
S2p=(2p-1) (2p-3)....x 1x[2p (2p-2)x ... x 2] / [2p (2p-2)x ... x 2]2 p/2.
S2p=(2p) ! / (2p p!)2 p/2.
De même :
S2p+1=(2p) / (2p+1) S2p-1 .
S2p+1= 2p (2p-2) / [(2p+1)(2p-1)] S2p-3 .
S2p+1=(2p (2p-2) (2p-4)S2p-5 / [(2p+1)(2p-1) (2p-3)] = ... =2p (2p-2)....x2 / [(2p+1) (2p-1)x ... x 3] S1.
S2p+1=[(2p (2p-2) (2p-4)]2 / [ [(2p+1) (2p-1)x ... x 3][(2p) (2p-2)x ... x 2] ]
S2p+1=(2pp!)2 / (2p+1)! .
|