Une
loi de probabilités,
Concours CAPLP maths sciences 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
On considère la fonction g définie sur l’intervalle [0; p] par g(x) = 15 / 16 sin5(x) et sa courbe C dans un repère orthogonal.
16. Dans cette question, on cherche l’expression d’une primitive de la fonction g sur [0; p].
a. Rappeler la formule générale du binôme de Newton.
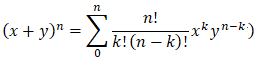
b. Développer l’expression (eit−e-it)5.
n = 5 ; x = it ; y = -it.
(eit−e-it)5=e5it -5e4it e-it+10e3it e-2it-10e2it e-3it+5eit e-4it-e-5it.
(eit−e-it)5=e5it -5e3it +10eit -10e-it +5 e-3it-e-5it.
c. En déduire que pour tout réel x,
sin5(x) =1 / 16 sin(5x) -5/16 sin(3x) +5/8 sin(x).
eit= cos (t) + isin(t) ;e-it= cos (t) - isin(t) ;
(eit−e-it)=2i sin (t).
(eit−e-it)5=25i sin5 (t).
(eit−e-it)5= cos(5t) + i sin(5t) -5(cos(3t) -5 i sin(3t) +10(cos(t) + 10 i sin(t) -10(cos(t) +10 i sin(t) +5 (cos(3t) -5i sin(3t) -cos(5t) +i sin(5t).
Identifier les parties imaginaires : 2sin(5t)-10 sin(3t)+20 sin(t) = 25 sin5 (t).
sin5 (t) =1 / 16 sin(5t)-5 / 16 sin(3t)+5/8 sin(t).
sin5 (t) =g(x) = 15 / 16 (1 / 16 sin(5t)-5 / 16 sin(3t)+5/8 sin(t).
d. En déduire une primitive de la fonction g sur l’intervalle [0; p].
G(x) = 15 / 16[-1 / 80 cos(5t) +5/48 cos(3t)-5/8 cos(t) ]+ constante.
|
...
|
....
|
17.
a. Montrer que 15 / 16 [G(p)-G(0) ]=1.
G(p)-G(0) =-1 / 80 cos(5p) +5/48 cos(3p)-5/8 cos(p) -[-1 / 80 cos(0) +5/48 cos(0)-5/8 cos(0) ].
G(p)-G(0) =1 / 80-5 /48 +5 /8 +1 /80-5 /48 +5 /8 = 1 /40 -5 / 24+5 /4=(3-25+150) / 120=128 /120.
15 / 16 [G(p)-G(0) ] =128 x15 / (120 x16)=1.
b. En déduire que g définit la fonction densité de probabilité d’une variable aléatoire à densité.
Sur l'intervalle [0 ; p],
g(x) est continue et positive ; l'aire du domaine compris entre l'axe
des abscisses et la courbe C sur cet intervalle est égale à 1 ( unité
d'aire).
On note X la variable aléatoire de densité g et P la probabilité associée définie, pour tout t appartenant à [0 ; p] par P(X < t) =G(t) - G(0).
18. Montrer que P(X < 0,5 p)=P(X > 0,5 p)=0,5.
P(X < 0,5 p)=15 / 16 [G(0,5p)-G(0)] =15 / 16 [0+1/80-5/48+5/8]=15 / 16 (3-25+150)/ 240=15 / 16 x128 / 240=1920 /3840 =0,5.
P(X > 0,5 p)=15 / 16 [G(p)-G(0,5p)] =15 / 16 [1/80-5/48+5/8-0]=15 / 16 (3-25+150)/ 240=15 / 16 x128 / 240=1920 /3840 =0,5.
19. En admettant que P(X < 0,25 p)~0,02, donner une valeur approchée de P(X < 0,5 p<0,75 p).
Par raison de symétrie P(X < 0,5 p<0,75 p)~ 0,5-0,02~0,48.

20. Montrer qu’il existe un unique t0 appartenant à [0,25 p ; 0,5 p] tel que P(X < t0) = 0,3.
Sur [0,25 p ; 0,5 p], g(x) est strictement croissante, positive, de 0,178 à 0,938.
P(X < 0,25 p)~0,02 ; P(X < 0,5 p)=0,5.
D'après le théorème des valeurs intermédiaires, il existe un unique t0 appartenant à [0,25 p ; 0,5 p] tel que P(X < t0) = 0,3.
21. Par la méthode de votre choix, déterminer une valeur approchée de t0 à 0,01 près.
P(X < t0)=15 / 16 [G(t0)-G(0)] =0,3.
15/16G(0) = 15/16(-1 /80+5 /48 -5 /8 )= -0,5.
15 / 16 G(t0) +0,5 ~0,3 ; G(t0)~ -0,8533.
15 / 16[-1 / 80 cos(5t) +5/48 cos(3t)-5/8 cos(t) ]~0,8533.
-1 / 80 cos(5t) +5/48 cos(3t)-5/8 cos(t)~ -0,213

t0 ~1,35
22. Dans cette question, on cherche à calculer l’espérance de la variable aléatoire X.
a. Pour tout nombre k réel non nul, déterminer l’expression de l’intégrale suivante :
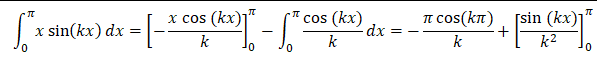
b. En déduire l’espérance de X.
g(x) = 15 / 16 (1 / 16 sin(5t)-5 / 16 sin(3t)+5/8 sin(t).
E(X) = -15 / 16 p [cos(5p) / 80-5 cos(3p)/48+5 cos(p) / 8]= -15/16p[-1/80 +5/48-5/8]~1,57.
|
|