Corrigé
mathématiques, exercices 1 et 2,
Concours CAPLP maths sciences 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exrcice 1. QCM.
1. Un fabriquant de
gâteaux souhaite faire des offres promotionnelles.
Affirmation
: « En tant que consommateur, il est préférable d’avoir une réduction
tarifaire de 20 % plutôt que 24 % de produit en plus pour le prix
initial ». Vrai.
Prix initial 1 € le kg.
Prix après réduction : 0,80 € le kg.
Prix avec 24 % de produit en plus : 1 / 1,24 =0,806 € le kg.
2. Un domino est
constitué de deux cases, chaque case contenant un nombre de points
compris entre 0 et 6.
Affirmation :
« Il y a 28 dominos différents ». Vrai.
0 0 ; 0 1 ; 0 2 ; 0 3 ; 0 4 ; 0 5 ; 0 6 ;
1 1 ; 1 2 ; 1 3 ; 1 4 ; 1 5 ; 1 6 ;
2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 ;
3 3 ; 3 4 ; 3 5 ; 3 6 ;
4 4 ; 4 5 ; 4 6 ;
5 5 ; 5 6 ; 6 6.
3. Soit (un)
la suite définie par u0=1,5 et, pour tout n entier naturel, un+1=2
/ (3-un) .
Affirmation :
« La suite vérifie l’inégalité : 1 < un < 2 ». Vrai.
u1=2 /1,5=4 /3 ; u2 =6 /5.
Initialisation : la propriété est vraie au rang zéro.
Hérédité : 1 <
un < 2
est supposée vraie.
Si un =1 ; un+1 = 1 ; Si un =2 ; un+1 = 2 ; 1 < un+1 < 2.
Conclusion : la propriété est vraie au rang 0 et héréditaire ; elle est
vraie pour tout entier naturel n.
4. Soit k un nombre entier
naturel non nul. On pose pour tout réel x, fk(x))=x-2+ke-x
et on note Ck sa courbe représentative. On admet que pour
tout entier naturel k non nul, la fonction fk admet un
minimum et on appelle Ak le point de la courbe Ck
correspondant.
Affirmation
: « Les points Ak appartiennent tous à une même droite ». Vrai.
Dérivée f 'k(x) =1-ke-x.
La dérivée s'annule pour e-x =1/k ; ex=k ; x =
ln(k) ; abscisse du minimum.
Ordonnée du minimum ; ln(k)-2 +1=ln(k)-1.
A1(0 ; -1) ; A2(ln(2) ; ln(2)-1) ;
A3(ln(3) ; ln(3)-1) ;
Les points Ak
appartiennent à la même droite : y = ax+b.
ln(k)-1= a ln(k)+b. a = 1 ; b = -1.
5. Un sujet
de physique est créé par l'un des trois professeurs M. Lavoisier, M.
Newton et M. Galilée. Statistiquement, on sait que 35 % des sujets sont
écrits par M. Lavoisier, 40 % sont écrits par M. Newton et que les
autres sujets sont écrits par M. Galilée. Les étudiants savent que 20 %
des sujets écrits par M. Lavoisier traitent de la relativité, que la
moitié des sujets écrits par M. Newton portent sur le thème de la
relativité et que 80 % des sujets écrits par M. Galilée portent sur le
thème de la relativité.
Lors de l’épreuve, ils découvrent un sujet sur le thème de la
relativité.
Affirmation
: « La probabilité qu’il ait été écrit par M. Newton est égale à 0,40
». Faux.

0,2 / 0,47 ~0,43.
6. La
fonction f désigne une fonction définie sur R qui vérifie, pour tous
réels x et y, f(x+y)=f(x)+f(y) et telle que la limite de f(h) / h tende
vers zéro si h tend vers zéro.
Affirmation
: « Seule la fonction identité répond à ces conditions ». Vrai.
7. On considère
l’équation différentielle 4y"−12y'+9𝑦=1.
Affirmation :
« Il existe une solution à cette équation différentielle qui est
strictement négative sur R ». Faux.
Equation caractéristique de 4y"−12y'+9𝑦=0 : 4r2-12r+9=0.
Discriminant D =
122-4*4*9=0 ; solution r = 12 / 8=1,5.
Solution générale de 4y"−12y'+9𝑦=0 : y = (a x+b) e1,5x
avec a et b réels.
Solution particulière de
4y"−12y'+9𝑦=1 : y = 1/9.
Solution générale : y = (a
x+b) e1,5x +1/9.
Pour a = b = -1 : y = -( x+1) e1,5x +1/9.
8. Le plan est muni d’un repère
orthonormé. On considère la droite d d’équation paramétrique
x=1−2t ; y=5−t, avec t réel et le cercle C de centre O (5 ;2) et de
rayon 4.
Affirmation
: « Le point A de la droite d de coordonnées (3 ; 6) dans le
repère est le point le plus proche du cercle C ». Faux.
Equation du cercle : (x-5)2+(y-2)2=16.
Le point le plus proche du cercle appartient à la tangente au cercle :
(3-5)2 +(6-2)2=4+16=20 diffère de 16.
9. Soit (un) une suite
définie par u0=2 et un+1=un / (1+un).
Affirmation
: « La suite (un) est décroissante minorée par 0 et converge
vers 0 ». Vrai.
un+1-un=un (1/ (1+un)-1)=un
(-un/
(1+un)) < 0. La suite
est décroissante.
u1=u0 /
(1+u0)=2/3 ; u1 =2 /5 ; u2 =2 / 7 .
un+1=1 / (1/un+1) tend vers zéro
si un tend vers zéro.
La suite est décroissante et minorée par zéro, donc elle converge vers
zéro.
.
10. Soit l’ensemble E des matrices
carrées de taille 2×2 à coefficients réels.
Affirmation :
« La matrice A= (12 02) est
diagonalisable dans E». Vrai.
Déterminant (A-l I)=(2-l)2-0 =0 d'ou l = 2.
La matrice de dimension 2 ne possède qu'une valeur propre, la matrice
n'est pas diagonalisable.
11. On considère la
proposition suivante : « Si deux matrices B et C carrées de taille 3×3
sont égales, alors pour toute matrice A carrée de taille 3×3, on a A x
B = A x C ».
Affirmation
: « La proposition réciproque est vraie ». Faux.
Si A est inversible : A-1 x A x B = A-1 x A x C
alors B = C.
Exercice 2.
Partie 1 : La fonction sinus.
1. Le plan est muni d’un
repère orthonormé. On note (C) le cercle trigonométrique de centre O et
Mx le point de (C) tel que x soit une mesure en radian de
l’angle orienté (i ; OMx). Rappeler la définition des
nombres cos(x) et sin(x) pour tout x réel.
Le cosinus de x noté cos(x) est l'abscisse de Mx.
Le sinus de x noté sin(x) est l'ordonnée de Mx.
2. Montrer que
l’aire d’un triangle dont on connaît l’un des angles et les longueurs des côtés
adjacents à cet angle est égale à :
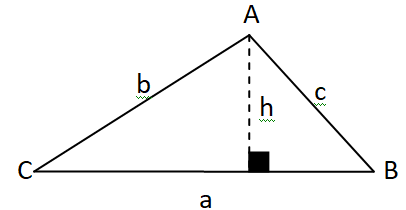
Aire = a h / 2 ; sin C = h / b dans le triangle rectangle de
gauche.
h = b sin C ; aire = a b sin C / 2.
3. En vous appuyant
la figure ci-dessous, démontrer à l’aide de la question précédente
l’égalité suivante :
sin(a + b) = sin(a) cos(b) + sin(b) cos(a) pour tous réels positifs a
et b vérifiant 0 < a + b < p.
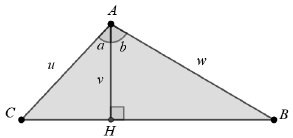
sin a = CH / u ; cos a = v / u ; sin b = BH / w ; cos b = v / w.
Aire du triangle ABC = u w sin (a+b) / 2.
Aire du triangle ACH = CH v / 2 = u v sin(a) / 2 ; aire du triangle ABH = BH v / 2 = w v sin(b) / 2.
u w sin
(a+b) = u v sin(a)
+w v sin(b).
sin (a+b) = v / w
sin(a) +v /
u sin(b).
v / w= cos (b) ; v / u = cos (a).
4. À l’aide de
l’exponentielle complexe, montrer que l’égalité de la question 3 est
vraie pour tous les réels a et b.
exp(i(a+b)) = exp(ia) x exp(ib).
exp(i(a+b)) =cos (a+b) + i sin(a+b).
exp(ia) = cos (a) + i sin(a) ; exp(ib) = cos (b) + i sin(b).
exp(ia) x
exp(ib)= cos (a) cos(b)-sin(a) sin(b) +i [cos (a) sin(b) +sin(a) cos(b)].
Identifier partie imaginaire et partie réelle.
|
...
|
....
|
Partie 2 : Étude d’une fonction.
On considère la fonction f définie sur R par f(x) = sin5(x).
On note C sa courbe dans le repère orthonormé (O; i, j).
5.a. Montrer que la
fonction f est 2p-périodique
et impaire sur R.
f(x) = sin4(x) sin(x); f(-x) =sin4(-x) sin(-x) =
-sin4(x) sin(x)= - f(x).
La fonction f est impaire.
f(x) =sin(x) *sin(x)*sin(x)*sin(x)*sin(x) ; sin(x) = sin(x+2p).
La fonction f est 2p-périodique
b. Montrer que
pour tout t appartenant à [0; p/2], f(p/2-t) =f(p/2+t).
sin(p/2-t) = sin(p/2+t).
sin5(p/2-t)
= sin5(p/2+t).
c. Justifier que
l’étude de la fonction f peut être limitée à l’intervalle [0, p/2].
Soit a
appartenant à [0 ; p/2]
: sin (a) = - sin (p+a).
Soit a
appartenant à [p
;3 p/2] : sin (p/2+a)
= sin (a).
Pour tout t appartenant à [p;
3p/2] : sin(p/2-t) = sin(p/2+t).
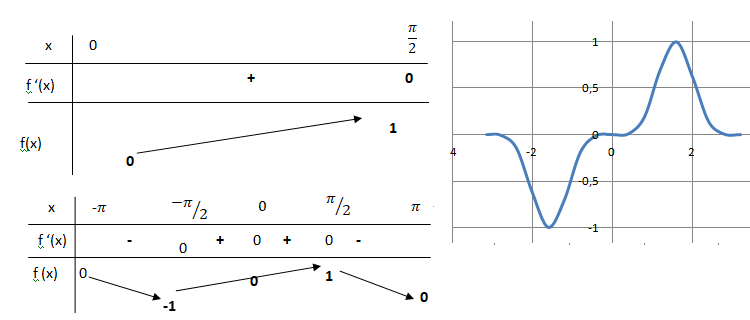
6. Dresser le
tableau de variation de la fonction f sur l’intervalle [0, p/2] et en déduire celui de
f sur l’intervalle [−p,
p].
f '(x) = 5 cos(x) sin4(x).
Le signe de f '(x) est celui de cos(x).
7. Déterminer
l’équation des tangentes à la courbe respectivement aux points
d’abscisse 0, d’abscisse p/4,
puis d’abscisse p/2.
f '(0) =0 ; équation de la tangente y = 0x+b ; f(0) = 0 ; b=0 ; y = 0.
f '(p/4 )=5 x0,7075
~0,88.
f(p/4 )=0,18 ;
équation de la tangente y = 0,88x +b ; 0,18 = 0,88 x3,14/4 +b ; b
=-2,58.
y = 0,88x -2,58.
f '(p/2 )=0.
f(p/2 )=1 ;
équation de la tangente y = b =1. y =
1.
8. Démontrer que la
fonction f admet un unique point d’inflexion sur l’intervalle [0, p/2].
Calcul de f ''(x) en posant u = cos (x) et v = sin4(x).
u' = -sin(x) ; v' = 4 cos(x) sin3(x).
f ''(x) = u'v+v'u = -sin5(x) +4 cos2(x) sin3(x)=sin3(x)
[4 cos2(x) -sin2(x)]=sin3(x) [4 cos2(x)
-(1-cos2(x)]=sin3(x) [ 5cos2(x)-1].
Sur l’intervalle [0, p/2].
:
sin3(x) croît de 0 à 1.
5cos2(x)-1 s'annule et change de signe pour x ~63,4 °.
9. Représenter une
allure de la courbe C de la fonction f sur l’intervalle [− p, p].
10. En utilisant la
méthode des rectangles à gauche et à droite avec 5 rectangles dont la
longueur de la base est de p/10,
donner un encadrement
de 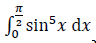 . .
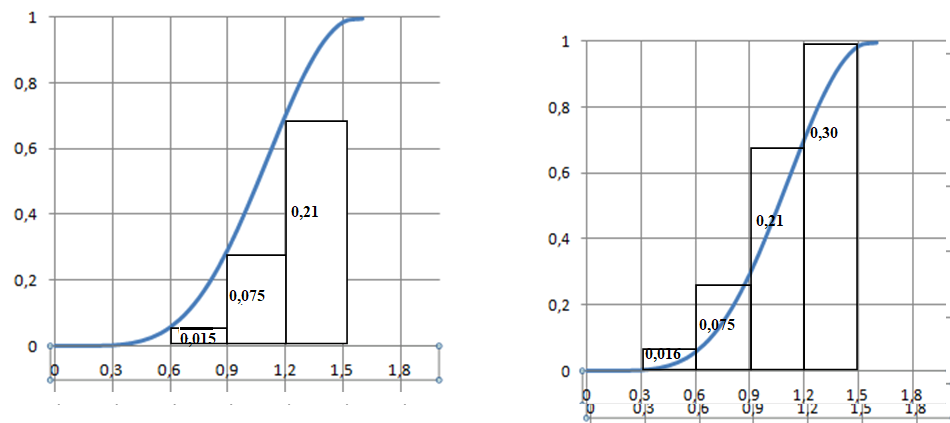
0,30 <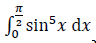 < 0,60. < 0,60.
|
|