Physique
chimie,
BTS 2023 bioanalyses et controles.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
L'acide tartrique. Partie A . Découverte de la chilarité. (8,5 points). 1. Définir les termes "dextrogyre" et énantiomères.
Les substances dextrogyres font tourner le plan de polarisation de la lumière polarisée vers la droite.
Les énantiomères sont des molécules, image l'une de l'autre dans un miroir plan.
2. Dessiner en représentation de Fischer la forme L(+) de l'acide tartrique.
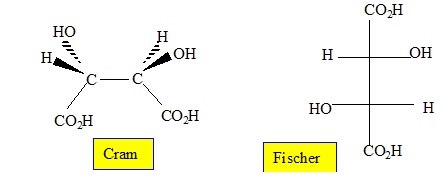 3.
3.4. Entourer et nommer les groupes fonctionnels de cette molécule. Repérer par un astérisque les atomes de carbone asymétriques.
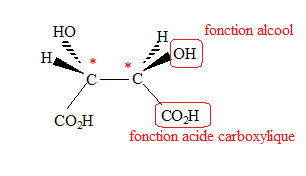 5.
5. Déterminer la configuration absolue de ces atomes de carbone. 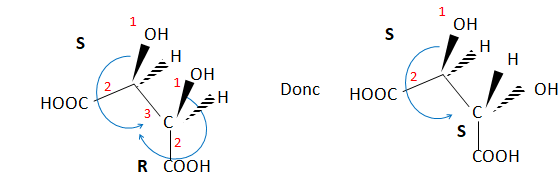 6.
6. Sur le spectre IR de la forme D(-) de l'acide tartrique. Identifier les deux bandes (a) et (b).
(a) bande large et forte vers 3300 cm -1 : O-H alcool lié
(b) : bande fine et forte vers 1750 cm -1 : C=O acide.
B. Réactions autour de l'acide tartrique ( 7 points).
L'acide tartrique C4H6O6 peut être obtenu par oxydation de l'acide maléique C4H4O4 par du permanganate de potassium en milieu basique.
7. Ecrire les deux demi-équations d'oxydoréduction ( en milieu acide pour simplifier) et en déduire l'équation de la réaction.
MnO4-aq / Mn2+aq : 2 fois { MnO4-aq + 8H+aq +5e- = Mn2+aq +4H2O(l). }
C4H6O6 / C4H4O4 : 5 fois {C4H4O4 +2H2O(l)= C4H6O6 aq + 2H+aq +2e- .}
2MnO4-aq + 16H+aq +10e- +5C4H4O4 +10H2O(l)= 2Mn2+aq +8H2O(l) + 5C4H6O6 aq + 10H+aq +10e-.
2MnO4-aq + 6H+aq +5C4H4O4 +2H2O(l)= 2Mn2+aq + 5C4H6O6 aq .
L'acide maléique et l'acide fumarique sont deux diastéréoisomères
correspondant à l'acide but-2-ène-1,4-dioique. L'acide maléique est de
configuration Z, l'acide fumarique est de configuration E.
8. Représenter ces isomères.
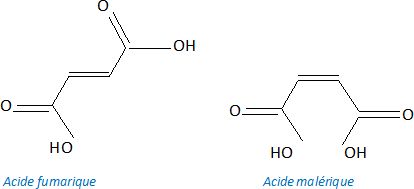
En présence d'éthanol en excès,
en milieu acide, l'acide tartrique subit une double estérification.
L'ester obtenu a pour formule brute C8H14O6.
9. Ecrire l'équation de cette réaction.

10. Identifier A et E.
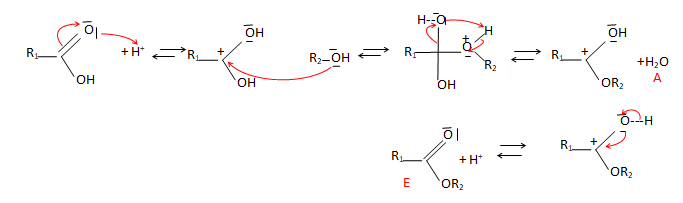
11. Quel est le rôle de H+ ?
Catalyseur.
|
| .
. |
....
|
Partie C. Polarimétrie. 7 points
Un technicien prépare une solution S1 d'acide L(+) tartrique de concentration c1
= (150 ±3) g / L. Il souhaite contrôler cette concentration par
polarimétrie. Il prépare une gamme étalon à partir d'une solution mère
de concentration 200 g / L ( 200 kg m-3)..
En utlisant un tube de longueur L = 30,0 cm, il mesure le pouvoir rotatoire a de chaque solution. L'incertitude type de la mesure est 0,06°.
c(g/L)
|
0
|
40
|
80
|
120
|
160
|
200
|
a(°)
|
0
|
1,5
|
3,1
|
4,4
|
6,1
|
7,3
|
12. Le pouvoir rotatoire spécifique [a] de l'acide L(+)-tartrique vaut +0,125° m2 kg-1. Que signifie le signe + ?
Déviation du plan de polarisation de la lumière polarisée vers la droite.
13. Vérifier
que ces mesures suivent la loi de Biot et concordent avec la valeur du
pouvoir rotatoire spécifique de l'acide l(+) - tartrique.
Loi de Biot : a = [a] L C.
a en degré ; [a] =0,125 ° m2 kg-1. L longueur du tube en m. C concentration en kg m-3.
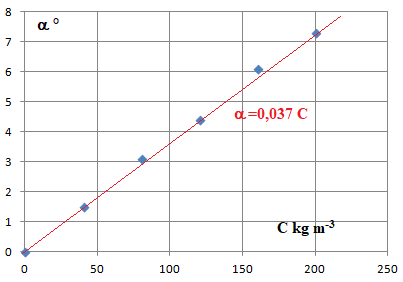
La loi de Biot est bien vérifiée.
[a] L= 0,125 x 0,30=0,0375 m3 kg-1.
14. Déterminer la concentration massique de la solution S1. Il mesure a = 5,6°pour la solution S1.
C = a / ( [a] L)=5,6 / 0,037=151 kg m-3.
u(C) = C u(a) / a =151 x 0,06 / 5,6=1,6 ~2.
C = (151±2) kg m-3.
La préparation du technicien est valide.
Partie D. Titrage pHmétrique de l'acide tartrique. (6,5 points).
On dilue 10 fois la solution S1. On dose V1 = 5,0 mL de S1 diluée par une solution d'hydroxyde de sosium telle que Cb =0,10 mol / L.
16 Comment préparer 50,0 mL de solution S1 diluée ?
Fiole jaugée de 50,0 mL. prélever 5,0 mL de solution S1 à l'aide d'une pipette jaugée. Verser dans la fiole jaugée. Compléter avec de l'eau distillée jusu'au trait de jauge. Agiter.
pKa1(C4H6O6 / C4H5O6-) = 3,04 ; pKa2( C4H5O6- / C4H4O6 2-) = 4,37.
17. Pourquoi n'observe t-on qu'un seul saut de pH ?
Les 2 pKa sont très proches l'un de l'autre.
18. Déterminer le volume équivalent.
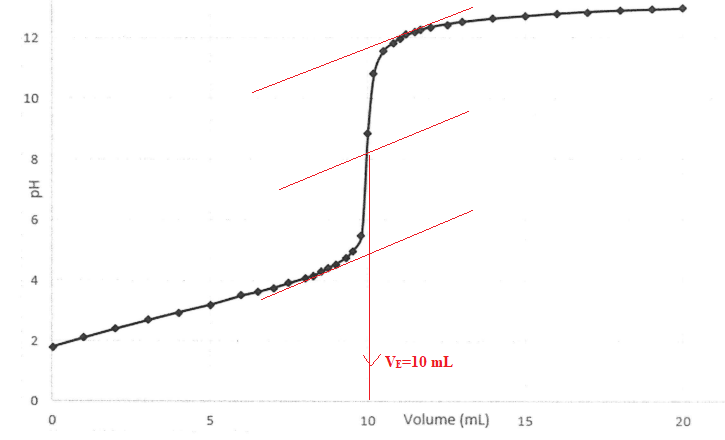
19. Quelle est la concentration C1 de la solution S1 ?
C4H6O6 aq + 2HO-aq --> C4H4O6 2-aq + 2H2O.
A l'équivalence : n(HO-)=2n(C4H6O6 ).
CbVE = 2 C1dilué V1.
C1dilué =CbVE / (2 V1) =0,1 x 10 / (2 x5,0) =0,1 mol / L ; C1 = 10 C1dilué =1,0 mol / L.
La préparation du technicien est valide.
Partie E.Solubilité de l'hydrogénotartrate de potassium KC4H5O6( 4,5 points).
M(KC4H5O6) = 188,2 g / mol ; produit de solubilité Ks = 9,2 10-4.
20. Equation de la dissolution de ce solide dans l'eau.
KC4H5O6(s) -->K+aq + C4H5O6- (aq).
21.22. Exprimer la solubilité s en fonction de Ks puis la calculer en g / L.
Ks = [K+aq] [C4H5O6- (aq)] =s2.
s = (9,2 10-4)½=3,03 10-2 mol / L.
3,03 10-2 *188,2 =5,7 g / L.
Partie F. Etude des cristaux d'acide tartrique au microscope ( 6,5 pts).
Taille d'un cristal d'acide tartrique : AB = 100 µm.
Microscope : objectif f '1 = 4,0 mm ; oculaire f '2 = 2,0 cm. Intervalle optique D=16,0 cm.
Distance minimale de vision distincte dm = 25 cm.
23. Indiquer la position de l'image intermédiaire pour avoir l'image définitive à l'infini.
L'image intermédiaire A1B1 se trouve au foyer objet de l'oculaire.
24. Calculer le grossissemant commercial.
G = D dm / (f '1 f '2) =0,16 x 0,25 / (4 10-3 x 2 10-2)=500.
25. Montrer que l'angle q sous lequel on voit la cristal à l'oeil nu à la distance dm vaut 4 10-4 rad.
tan q ~q =AB / dm = 100 10-6 / 0,25 =4 10-4 rad, proche du pouvoir séparateur de l'oeil 310-4 rad, donc la résolution sera médiocre.
26. Calculer l'angle q' sous lequel est vu le cristal à travers le microscope.
q' = G q = 500 x 4 10-4 =0,2 rad. la résolution est bien meilleure.
|
|