Mathématiques, Amérique du Sud, DNB 2023.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Exercice1.  (20 points).

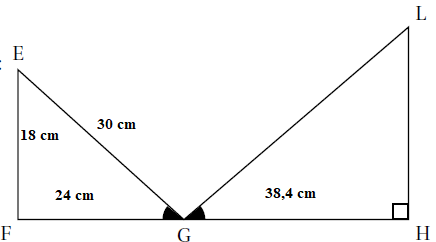1. Montrer que le triangle EFG est rectangle en F.
EF2 +FG2 =152+242= 900 ; EG2 = 302 = 900.
EF2 +FG2 =EG2 . La relation de Pythagore étant vérifiée, le triangle EFG est rectangle en F.
2. Calculer la mesure de l’angle EGF. Donner l’arrondi au degré près.
tan EGF = EF / FG = 18 / 24 =0,75.
Cet angle mesure environ 37 °.
3. Montrer que les triangles EGF et LGH sont semblables.
Des triangles ayant des angles deux à deux égaux, sont semblables.
4. Quel est le coefficient d’agrandissement qui permet de passer du triangle EFG au triangle LHG ?
GH / FG = 38,4 / 24 =1,6.
5. Quel est le périmètre du triangle LGH ?
Périmètre du triangle EFG : 30 +18 +24 = 72 cm.
Périmètre du triangle LGH : 1,6 x 72 =115,2 cm.
.
Exercice 2 21 points.

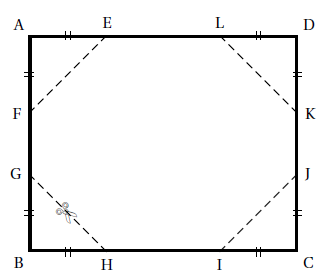
À partir d’une feuille rectangulaire de dimension 10 cm sur 8 cm, on coupe les quatre coins de manière
identique.
On obtient ainsi un polygone FELKJIHG et quatre triangles rectangles isocèles égaux
AD = 10 cm; AB = 8 cm.
Les deux parties sont indépendantes.
Première partie : on suppose que AE = 3 cm.
1. Quelle est l’aire du triangle AEF ?
AE x AF / 2 = 3 x3 / 2 = 4,5 cm2.
2. En déduire l’aire du polygone FELKJIHG.
10 x 8 -4 x4,5 = 80-18=62 cm2.
Deuxième partie :
On souhaite que l’aire du polygone FELKJIHG soit de 60 cm2.
Pour cela, on fait varier la longueur AE et on observe l’effet sur l’aire du polygone FELKJIHG.
On note x la longueur AE exprimée en cm.
3. a. Exprimer l’aire du triangle AEF en fonction de x.
A = 0,5 x2.
b. Montrer que l’aire du polygone FELKJIHG, en cm2, est donnée par l’expression 80−2x2.
8 x10 -4A = 80 -4 x0,5 x2 = 80-2x2.
4. On considère la fonction f : f(x)= 80−2x2.
À l’aide d’un tableur, on a produit le tableau de valeurs ci-dessous :

 A
 B
 C
 D
 E
 F
 G
 H
 I
 J
1
 x
 0
 0,5
 1
 1,5
 2
 2,5
 3
 3,5
 4
2
 f(x)
 80
 79,5
 78
 45,5
 72
 67,5
 62
 55,5
 48
Proposer une formule qui a pu être saisie en B2 avant d’être étirée vers la droite.
=80-2*B1*B1
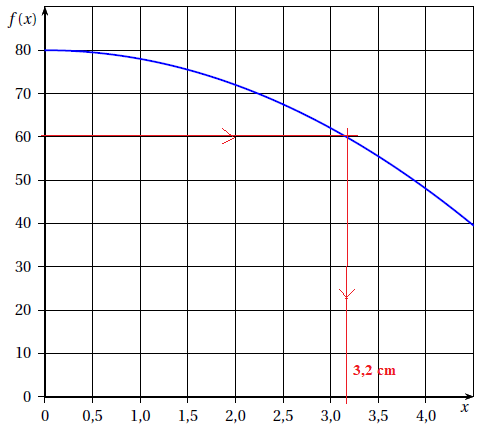
5. Voici la courbe représentative de la fonction f :

a. La fonction f est-elle affine?
Non, le graphe n'est pas une droite.
b. Par lecture graphique, déterminer une valeur approchée de la longueur AE permettant d’obtenir un polygone FELKJIHG d’aire égale à 60 cm2.
c. Trouver par le calcul la valeur exacte de cette longueur.
60 = 80 -2x2 ; 20 = 2x2 ; x2 = 10 ; x = 10½~3,16 cm.

Exercice 3. 20 points.
Pour chacune des affirmations, indiquer si elle est vraie ou fausse en justifiant la réponse.
1. On considère le tableau ci-dessous :
Nombre de baguettes
 1
 2
 3
 4
Prix en €
 1,10
 2,20
 3,30
 4
Affirmation 1 : « Le prix est proportionnel au nombre de baguettes. »
Vrai pour l'achat de 1, 2 ou 3 baguettes ; Faux pour l'achat de 4 baguetttes.
2. On considère ci-dessous le point A sur une droite graduée :

Affirmation 2 : « L’abscisse du point A est un nombre décimal. »
2 + 2 x0,125 = 2,25. Vrai.
3.On considère cet engrenage qui est composé d’une roue A à 8 dents et d’une roue B à 12 dents.

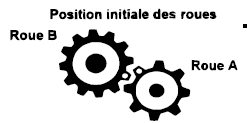
Affirmation 3 : « Cet engrenage sera dans la même position au bout de 6 tours pour la roue A et de 4 tours pour la roue B. »
6 x8 = 4 x12 = 48. Vrai.
4. Affirmation 4 :
« Pour tout nombre x, l’égalité suivante est vraie :
(x +8)(2x −1) =2x2 −(8−15x).
(x +8)(2x −1) =2x2-x+16x-8=2x2+15x-8=2x2 −(8−15x). Vrai.

.
.
....

 Exercice 4 16 points
Une usine fabrique des bougies parfumées en cire de forme cylindrique.
Les questions 1, 2 et 3 sont indépendantes.

Une bougie est composée de cire et de parfum.
Le volume de cire nécessaire à la fabrication d’une bougie correspond au 9 / 10 du volume de cette bougie.
1 cm3 de cire a unemasse de 0,7 g.
1. a. Montrer que le volume d’une bougie est d’environ 339 cm3.
pr2h=3,14 x 32 x12~339 cm3.
b. Quelle est la masse de cire nécessaire pour une bougie ? On donnera une valeur approchée au gramme près.
Volume de cire : 339 x9 / 10 ~305 cm3.
Masse de cire : 305 x0,7 ~214 g.
2. Au mois de novembre, l’usine a fabriqué des bougies de 4 parfums différents :
vanille, miel, lavande et jasmin.
Les bougies au miel représentent 22% de la production du mois de novembre.
Quel est le pourcentage de bougies à la lavande fabriquées au mois de novembre?

Production du mois de novemnre : N ;
nombre de bougies à la vanille : 0,25 N soit 25 %.
nombre de bougies à la lavande = nombre de bougies au jasmin = N (1-0,22-0,25) / 2 =0,265 N soit 26,5 %.

3. Durant les trois premiers mois de l’année suivante, l’entreprise se donne pour objectif de produire en moyenne 7 900 bougies par mois.
En janvier, elle fabrique 6 500 bougies et 8 000 en février.
Quel est le nombre de bougies à produire en mars pour atteindre l’objectif ?
Nombre moyen de bougies fabriquées en 3 mois : 3 x7900 =23 700.
Production de mars : 23 700 -6500 -8000 =9 200.

Exercice 5. 23 points.
On dispose d’une roue dont les 4 secteurs ont tous la même aire et sont numérotés : 1; 2; 3; 4.
On dispose également d’une urne contenant 3 boules numérotées : 2 ; 3 et 4.
Les boules sont indiscernables au toucher.
On considère l’expérience aléatoire suivante :
« On fait tourner la roue puis on tire au hasard une boule dans l’urne. On forme alors un nombre entier à deux chiffres tel que :
• Le chiffre des dizaines est le numéro indiqué par la flèche sur la roue.
• Le chiffre des unités est le numéro de la boule tirée dans l’urne. »
Exemple : Si la flèche indique le numéro 1 sur la roue et que la boule tirée dans l’urne porte le numéro 3, on forme le nombre 13.
1. Écrire la liste des 12 issues possibles.
12 ; 13 ; 14 ; 22 ; 23 ; 24 ; 32 ; 33 ; 34 ; 42 ; 43 ; 44.
2. Déterminer la probabilité de l’évènement : «Obtenir un nombre impair ».
13 ; 23 ; 33 ; 43 soit 4 possibilités sur 12 : probabilité de tirer un nombre impair = 0,25.
3. On considère l’évènement A : « Le nombre formé est un nombre premier et inférieur à 30 ».
a. Quelle est la probabilité de l’évènement A?
13 ; 23 : p(A = 2 /12 = 1 / 6.
b. Quelle est la probabilité de son évènement contraire ?
1-1 /6 = 5 / 6.
À l’aide de cette expérience aléatoire, on crée un jeu de hasard.
Le joueur gagne s’il obtient un multiple de 11.
4. Montrer que la probabilité d’obtenir un multiple de 11 est égale à 0,25.
22 ; 33 ; 44 soit 3 possibilités sur 12 ; probabilité de gagner : 3 / 12 = 1/4 = 0,25.
5. On souhaite simuler ce jeu à l’aide d’un logiciel de programmation.
On a rédigé le script ci-dessous :

a. Écrire sur la copie comment compléter les deux cases vides de la ligne 5. Ne pas justifier.
b. Écrire sur la copie comment compléter les deux cases vides de la ligne 6. Ne pas justifier.

c. On a cliqué sur le drapeau et voici le résultat du programme :
« La fréquence d’apparition d’un multiple de 11 est 0,23. »
Pourquoi le résultat est-il différent de celui obtenu dans la question 4 ?
Plus le nombre de tirages est grand, plus la proportion de multiples de 11 se rapproche de 0,25.

  
menu