Mathématiques, DNB Polynésie 09 /2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice1. QCM (16 points). 1. 1. Une augmentation de 9% correspond à une multiplication par . . .. 1+ 9 / 100 = 1,09. Réponse C. 2. On considère la figure ci-dessous. On précise que : • (DE) et (BC) sont parallèles; • E est un point de [AC] ; • D est un point de [AB] ; • E = 2 cm, EC = 5 cm, ED = 3 cm. Quelle est la longueur BC? 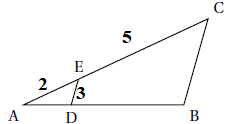Relation de Thalès : BC / ED = AC / AE = 7 / 2 = 3,5.. BC = 3,5 ED = 3,5 x 3 = 10,5 cm. . Réponse C. 3.  Le tableau ci-dessous donne la répartition des élèves de 5e d’un collège en fonction du sexe et de la langue vivante 2 choisie : allemand espagnol italien filles 10 43 26 garçons 7 42 32 On interroge au hasard un élève de 5e parmi tous les élèves de 5e de ce collège. Quelle est la probabilité que l’élève interrogé ait choisi l’italien en deuxième langue vivante? (26 +32) / (10+7+43+42+26+32) =58 / 160~0,36. Réponse B. 4. On reprend la situation de la question 3. et on interroge au hasard un élève de 5e parmi tous les élèves de 5e de ce collège. Quelle est la probabilité que l’élève interrogé soit une fille qui ne fait pas d’allemand ? (43+26) / 160 =69 / 160 . Réponse C. Exercice 2 25 points 1. On considère le programme A défini par le schéma ci-dessous : 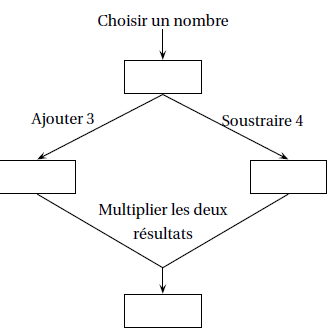a. Vérifier que le résultat est 60 si le nombre choisi au départ est −8. -8-4 = -12 ; -8+3= -5 ; -12 x(-5) = 60. b. On appelle x le nombre de départ et on admet que le résultat obtenu avec le programme de calcul est donné par l’expression : (x +3)(x −4). Résoudre (x +3)(x −4) =0. x+3 =0 soit x = -3 ; x-4 =0 soit x = 4. En déduire quels nombres de départ il faut choisir pour obtenir 0 comme résultat. Il faut choisir 4 ou -3. 2. On rappelle que x désigne le nombre de départ du programme de calcul et que le résultat obtenu avec le programme de calcul est donné par l’expression : (x +3)(x −4). On appelle f la fonction qui, à x, associe le résultat du programme de calcul. La représentation graphique Cf de la fonction f est donnée. a. Montrer que f (x) = x2−x −12. (x+3)(x-4) = x2+3x-4x-12 = x2−x −12. b. Calculer f(0,5). f(0,5) = 0,52 -0,5 -12 = -12,25. c. Déterminer graphiquement les antécédents de −6 par la fonction f . 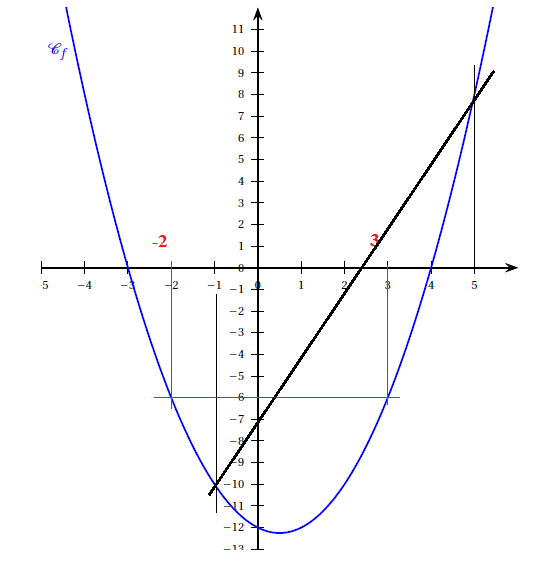2. On considère la fonction g définie par g(x) =3x −7. On a utilisé un tableur pour réaliser un tableau de valeurs de cette fonction. A B 1 x g(x) 2 -5 -22 3 -3 -16 4 -1 -10 5 5 8 a. Quelle formule a-t-on écrite dans la cellule B2 avant de l’étirer vers le bas? =3*A2-7 b. Tracer la représentation graphique de la fonction g. c. Déterminer graphiquement les nombres qui ont la même image par les fonctions f et g. -1 et 5 Exercice 3. 19 points. Dans cet exercice, toutes les longueurs sont exprimées en pixel. Un professeur de mathématiques souhaite élaborer un programme avec ses élèves permettant de construire la figure ci-contre composée de 10 carrés. Le côté du premier carré à trace rmesure 300 pixels. Le côté de chaque carré construit ensuite mesure 20% de moins que celui du carré précédent. La figure n’est pas en vraie grandeur. Aucune justification n’est attendue pour les questions 2., 3. a., 3. b. et 4. 1. Montrer que le côté du 2e carré mesure 240 pixels. 300 -0,2 x 300 =240 pixels. 2. Le professeur distribue aux élèves le bloc « Carré »d’instructions qui permet de tracer un carré de côté donné. Pour cela, il a créé une variable «Côté » qui correspond à la longueur du côté du carré à tracer. Compléter les lignes 2 et 4 de ce bloc. 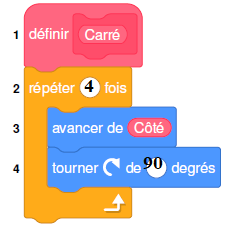3. Le script ci-dessous permet de réaliser les dix carrés de la figure souhaitée. On rappelle que l’instruction « s’orienter à 180 » signifie que le lutin est dirigé vers le bas. a. Donner les coordonnées du stylo lorsqu’il commence à tracer le premier carré. 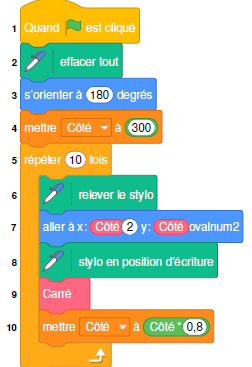x = 300 ; y =300. 3. b. Parmi les 4 propositions suivantes, quelle est celle qui correspond au tracé des deux premiers carrés ? 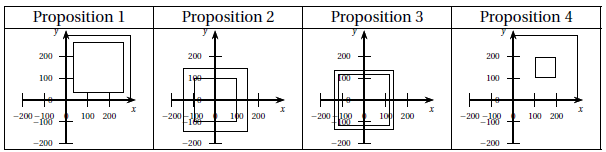Proposition A. c. Quelle est la longueur du dernier carré tracé avec le script précédent ? Arrondir au pixel.  300x0,89~40 pixels. 4. On veut diminuer l’épaisseur des traits lorsqu’on passe de la construction d’un carré au suivant pour obtenir la figure suivante. Pour cela, on souhaite utiliser les deux instructions suivantes : • Instruction A : ajouter −1 à la taille su stylo • Instruction B : mettre la taille du stylo à 11 Pour chaque instruction, indiquer les numéros des lignes du script de la question 2 entre lesquelles elle peut être insérée afin d’obtenir cette figure. Entre la ligne 9 et la ligne 10. . . .... Exercice 4 20 points Les propriétaires d’une maison souhaitent créer une rampe d’accès à leur terrasse. Cette rampe devra avoir la forme d’un prisme droit à base triangulaire comme représenté sur le schéma en perspective cavalière ci-dessous : Les figures ci-dessus ne sont pas à l’échelle. On donne les informations suivantes : • la hauteur [AC] de la rampe mesure 30 cm ; • AB = 124 cm; • la longueur BE de la rampe mesure 9 m; • l’angle ACB est un angle droit. 1. Déterminer la mesure de l’angle ABC que doit faire la rampe avec le sol du jardin. On arrondira au degré près. Sinus de cet angle = AC / AB = 30 / 124=0,242. Cet angle mesure environ 14°. 2. Montrer que la longueur BC doit être environ égale à 120 cm. BC2 + AC2 = AB2 ; BC2  = AB2 - AC2= 1242-302=14 476 ; BC ~120 cm. 3. Pour réaliser cette rampe, les propriétaires envisagent de se faire livrer 2 m3 de béton. Ce volume est-il suffisant ? Aire du triangle ABC : AC x BC / 2 = 0,30 x 1,20 /2 = 0,18 m2. Volume de béton = aire du triangle ABC x BE =0,18 x 9 = 1,62 m3. Le volume  de 2 m3 sera sufisant. 4. En utilisant le volume de 2 m3 de béton, sans modifier les longueurs AC et BE de la rampe, quelle serait la valeur de BC ? On arrondira au centimètre près. Aire du triangle ABC  = 2 / BE = 2 / 9 m2. 2 / 9 = AC x BC / 2 ; BC = 4 / (9 AC) = 4 /(9 x 0,3) =1,48 m. Exercice 5 20 points. La transat Jacques Vabre est une course de bateaux qui relie la ville du Havre, en France métropolitaine, à la ville de Fort-de-France, en Martinique. 1. Avec la précision permise par la carte, donner la latitude et la longitude de la ville de Fort-de- France repérée par une croix sur la carte ci-dessus. Latitude : 15 ° nord ; longitude : 62° ouest. 2. Lors de l’édition 2021, 75 bateaux ont participé à cette course, répartis dans quatre catégories en fonction du parcours à réaliser : Class 40, Ocean Fifty, Imoca, Ultim. Le tableau ci-dessous présente les catégories, les effectifs engagés, les distances parcourues et le palmarès de la Transat : nombre de bateaux de la catégorie distance du parcours nom du bateau vainqueur de la catégorie durée de la course du vainqueur class 40 43 4600 milles Redman 21 jours 22 heures 33 minutes ocean Fifty 7 5800 milles Primordial 15 jours 13 heures 27 minutes imoca 20 5800 milles linkedout 18 jours 1 heure 21 minutes ultim 5 7500 milles Maxi Edmond de Rothschild 16 jours 1 heure 48 minutes Information : Un mille nautique est une unité demesure marine qui équivaut à 1,852 km environ. a. Montrer que le bateau LinkedOut met 2 jours 11 heures et 54 minutes de plus que le bateau Primonial pour effectuer son parcours. 18 jours 1 heure 21 minutes - 15 jours 13 heures 27 minutes. 17 jours 25 heure 21 minutes - 15 jours 13 heures 27 minutes. 17 jours 24 heure 81 minutes - 15 jours 13 heures 27 minutes. Soit 2 jours 11 heures 54 minutes. b. Calculer la moyenne des distances parcourues par l’ensemble des 75 bateaux. On arrondira cette distance à l’unité près. (43 x 4600 +27 x5800 +5 x7500 ) / 75=(197 800 +156 600 +37 500 ) / 75=5 225 milles. c. La vitesse moyenne du bateau Redman a été d’environ 8,7 milles / h. Montrer que la vitesse moyenne du bateau Maxi Edmond de Rothschild a été environ 2,2 fois plus grande que celle du bateau Redman. 16 jours =16 x24 heures =384 heures. 48 / 60=0,8 heure. Durée : 384 +1+0,8 =385,8 heures. Vitesse de ce bateau = 7500 / 385,8=19,4 milles / heure. 19,4 / 8,7 ~2,2. d. Un journaliste affirme que la distance parcourue par un bateau de la catégorie Ocean Fifty est environ égale à un quart de périmètre de l’équateur de la Terre. En sachant que le rayon de l’équateur est de 6 370 km, le journaliste a-t-il raison ? 5800 x1,852=10 741,6 km. Circonférence de la Terre à l'équateur : 2 x3,14 x 6370=40 024 km. 40 024 / 4 =10 006 km. Le journaliste a raison.

menu