Mathématiques, DNB Métropole Antilles 09 / 2023.

Exercice1. QCM (20 points).
1. Citer trois diviseurs de 84.
84 = 2² x3 x7.
Réponse B : 2, 3 et 4.

2. La pyramide SABCD est un agrandissement de coefficient 2 de la pyramide SA′B′C′D′.
Par quel nombre doit-on multiplier le volume de la pyramide SA′B′C′D′ pour obtenir le volume de la pyramide SABCD?

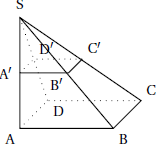
Volume = 1 /3 base x hauteur.
La base est multipliée par 4 et la hauteur par 2. Le volume sera multiplié par 8. Réponse B.
3. Quelle est la valeur de l’expression : x² +3x-5 pour x =2.
2² +3*2 -5 =5. Réponse B.
4. Dans un sac opaque, on dispose de huit boules numérotées de 1 à 8.
On tire une boule au hasard. Quelle est la probabilité d’obtenir un multiple de 2?
2 ; 4 ; 6 ; 8 soit 4 possibilités sur 8.
Probabilité de tirer un multiple de 2 : 4 / 8 = 0,5. Réponse A.
5. Le triangle DEF est l’image du triangle ABC par une homothétie de centre O. Quel est son rapport ?

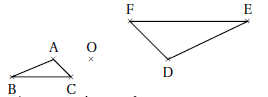
OD / OA = 2.
A et D sont situés de part et d'autre de 0. Le rapport d'homothétie vaut -2. Réponse A.

Exercice 2 14 points
1. On souhaite tracer le losange ci-dessous de côté 50 pas à l’aide du bloc losange.
On a écrit le script ci-dessous avec le logiciel Scratch. Recopier les lignes 3 et 6 sur la copie en les complétant.

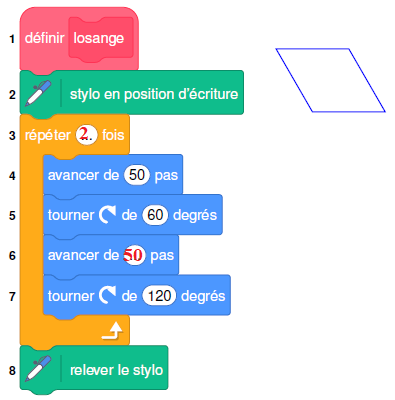2. Préciser sur votre copie quelle figure est associée à chaque script 1, 2 ou 3. Aucune justification n’est demandée.

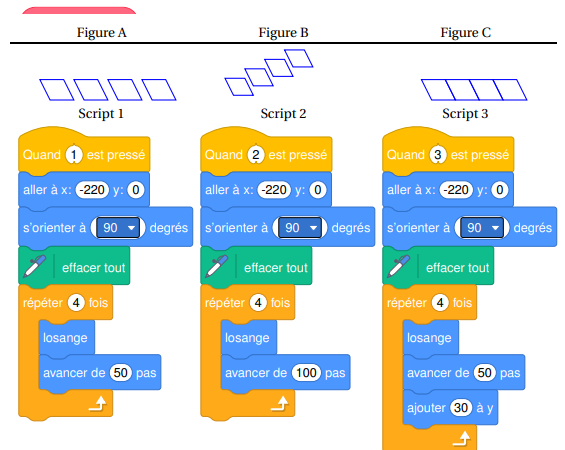
Association des scripts : Script 1 figure C ; Script 2 figure A ; Script 3 figure B.

3. Dans la figure ci-dessous obtenue par le programme associé, décrire une transformation qui permet d’obtenir le losange ABCD à partir du losange EDCF. Préciser ses caractéristiques.

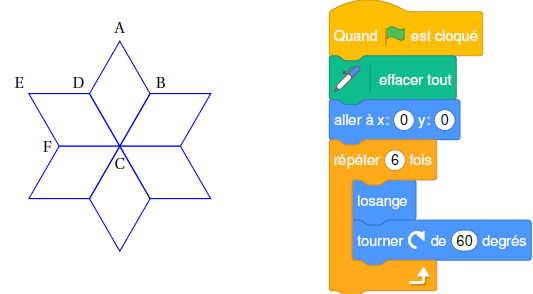
Rotation d'angle 60° et de centre C.

Exercice 3. 22 points.
Une piscine propose deux tarifs d’entrée pour l’année 2023.
Tarif A : 5,90 € l’entrée.
Tarif B : 4,40 € l’entrée avec une carte d’abonnement de 30 € valable toute l’année.
1. a. Quel est le prix total pour 10 entrées avec le tarif A ?
10 x 5,9 = 59 €.
b. Quel est le prix total pour 10 entrées avec le tarif B ?
10 x4,4 +30 = 74 €.
2. On note f et g les fonctions qui modélisent les prix, en euro, respectivement du tarif A et du tarif B en fonction du nombre x d’entrées. Donner l’expression de f (x), puis celle de g(x).
f(x) = 5,9 x ; g(x) = 4,4 x +30.
3. a. Résoudre l’équation 5,90x = 4,40x +30.
5,9x-4,4x = 30 ; 1,5 x = 30 ; x = 30 / 1,5 ; x = 20.
b. Quel est le nombre d’entrées pour lequel les tarifs A et B donnent le même prix à payer ?
20 entrées.
4. On relève le nombre d’entrées par mois durant une année.

mois	jan	fév	mars	avril	mai	juin	juillet	aout	sept	oct	nov	déc
nombres d'entrées	12500	13700	10400	13600	12300	11700	10400	11600	10200	13800	12600	11800

a. Calculer le nombre moyen d’entrées par mois.
(12 500 +13700 +10400 +13600+12300+11700+10400+11600+10200+13800+12600+11800) / 12 = 12050.
b. Calculer l’étendue du nombre d’entrées par mois.
13800-10200=3600.
5. La piscine a la forme d’un pavé droit de longueur 50 m, de largeur 25 m et de profondeur 3 m.
En admettant qu’elle soit entièrement remplie, déterminer en m³, le volume d’eau qui sera évacué pour réaliser la vidange.
50 x 25 x 3 = 3 750 m³.