Mathématiques, DNB Métropole 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice1. (20 points). Un opticien vend différents modèles de lunettes de soleil. Il reporte dans le tableur ci-dessous des informations sur cinq modèles vendus pendant l’année 2022. A B C D E F G 1 Lunettes de soleil modèle 1 modèle 2 modèle3 modèle 4 modèle5 total 2 nombre de lunettes vendues 1200 950 875 250 300 3 prix unitaire 75 100 110 140 160 1. Montrer que l’étendue des prix de ces paires de lunettes de soleil est de 85 euros. 160 -75 =85 €. 2. a. Quelle formule doit-on saisir dans la cellule G2 pour calculer le nombre total de paires de lunettes de soleil vendues en 2022 ? =somme(B2:F2) b. Calculer le nombre total de paires de lunettes de soleil vendues en 2022. 3575. 3. a. Calculer le montant total, en euros, des ventes des paires de lunettes de soleil en 2022. 1200 *75 +950 *100 +875 *110 +250 *140 +300*160 =364 250 €. b. Calculer le prix moyen d’une paire de lunettes de soleil vendue en 2022, arrondi au centime près. 364 250 / 3575 =101,89 €. Exercice 2 20 points Sur la figure ci-dessous :  BCDE est un rectangle, BAE est un triangle rectangle en A ;  la perpendiculaire à la droite (CD) passant par A coupe cette droite en H ;  les droites (AE) et (CD) se coupent en F. On donne :  AB = BC = 4,2 cm ;  EB = EF = 7 cm. 1. Montrer que l’aire du rectangle BCDE est égale à 29,4 cm2. BC x EB = 4,2 x 7 =29,4 cm2. 2. a. Montrer que la longueur AE est égale à 5,6 cm. Relation de Pythagore dans le triangle rectangle ABE : BE2 = AB2 +AE2 ; AE2 = 72-4,22 =31,36 ; AE = 5,6 cm. b. Calculer l’aire du triangle rectangle ABE. AB x AE / 2 = 4,2 x5,6 / 2 = 11,76 cm2. 3. a. Montrer que les droites (ED) et (HA) sont parallèles. Les droites (ED) et (HA) sont toutes deux perpendiculaires à la droite (CD): elles sont donc parallèles. b. Calculer la longueur AH. Les droites (ED) et (HA) sont parallèles et les droites (CF) et (AF) sont sécantes. Relation de Thalès : AH / ED = AF / EF =HF / DF. AF = AE+EF =5,6 +7 = 12,6 cm. AH = AF x ED / EF =12,6 x 4,2 / 7 =7,56 cm. Exercice 3 QCM 20 points 1. Dans une classe de 25 élèves, 60 % des élèves sont des filles. Combien y a-t-il de filles dans cette classe ? 25 x 0,60=15. Réponse B. 2. Quelle est la décomposition en produit de facteurs premiers de 126 ? 126 = 2 x 32 x7. Réponse C. 3. Dans un sac, il y a 17 jetons rouges, 23 jetons jaunes et 20 jetons bleus, tous indiscernables au toucher. On tire au hasard un jeton du sac. Quelle est la probabilité d’obtenir un jeton rouge ou un jeton jaune ? (17 +23) / (17+23+20)=40 / 60 = 2 /3. Réponse A. 4. Sur l’octogone régulier ci-dessous, quelle est l’image du segment [DC] par la rotation de centre O qui transforme A en D ? 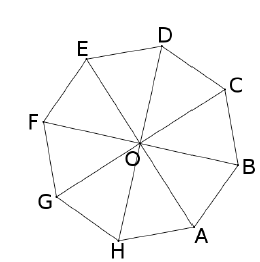Rotation de 3 x45 = 135° dans le sens anti-horaire. Segment GF. Réponse B. 5. Quel est le volume d’un pavé droit de hauteur 1,5 m et de base rectangulaire de 2 m de longueur et 1,3 m de largeur ? On rappelle que 1 m3 = 1 000 L. 2 x1,3 x1,5 =3,9 m3 = 3900 L. Réponse B. . . .... Exercice 4 20 points On veut fabriquer un escalier en bois de hauteur 272 cm. La figure ci-dessous représente une vue de profil de cet escalier. La hauteur d’une marche est de 17 cm. La profondeur d’une marche pour poser le pied mesure 27 cm. 1. a. Montrer qu’il faut prévoir 16 marches pour construire cet escalier. 272 / 17 =16. b. Montrer que la longueur AB est égale à 432 cm. 16 x 27=432 cm. 2. Pour permettre une montée agréable, l’angle BAC doit être compris entre 25° et 40°. a. Calculer la mesure de l’angle BAC, arrondie au degré près. Tan BAC = BC / AB = 272 / 432 =0,63. L'angle BAC mesure environ 32°. b. L’escalier permet-il une montée agréable ? Oui, 32 est compris entre 25 et 40°. 3. On rédige le programme ci-contre avec le logiciel Scratch pour dessiner cet escalier. (1 cm dans la réalité est représenté par 1 pas dans le programme.) Recopier les lignes 5, 6, 7 et 9 sur la copie en les complétant. Exercice 5 20 points Voici deux programmes de calcul. Programme A  Choisir un nombre. Multiplier ce nombre par −2.  Ajouter 5 à ce résultat. Programme B  Choisir un nombre. Soustraire 5 à ce nombre. Multiplier le résultat par 3. Ajouter 11 au résultat. 1. a. Montrer que, si on choisit −3 comme nombre de départ, le résultat obtenu avec le programme A est 11. -3 x(-2)+5=11. b. Quel résultat obtient-on avec le programme B si on choisit 5,5 comme nombre de départ ? (5,5-5)x3 +11 =12,5. 2. En désignant par x le nombre de départ, on obtient −2x+5 comme résultat avec le programme A. Montrer, qu’avec le même nombre de départ, le résultat du programme B est égal à 3x−4. (x-5) *3 +11 = 3x-15+11 = 3x-4. 3. a. On a représenté ci-contre les fonctions f et g définies par f(x)=−2x+5 et g(x)=3x−4. Associer, en justifiant, chaque droite à la fonction qui lui correspond. f(x) a un coefficient directeur négatif ; f(x) est décroissante, droite D2. g(x) a un coefficient directeur positif ; g(x) est croissante, droite D1. b. Par lecture graphique, donner le plus précisément possible, le nombre dont l’image est la même par la fonction f et la fonction g. f(1,8) = g(1,8). 4. Déterminer par le calcul le nombre de départ pour lequel les programmes A et B donnent le même résultat. -2x+5 = 3x-4 ; 3x+2x = 5+4 ; 5x = 9 ; x = 9 /5 =1,8.

menu