Mathématiques, DNB Centres étrangers 2023

Exercice 1 ( 18 points).
Partie A
Dans cette partie, on s'intéresse au programme ci-dessous, composé d'un bloc« triangle équilatéral» et d'un script principal.
1. Compléter le script du bloc principal.

Script principal	Bloc " triangle équilatéral"
aller à 0 ; 0 s'orienter à 90° effacer tout répéter 2 fois stylo en position écriture ... relever le stylo tourner de 60° dans le sens trigonométrique	stylo en position écriture répéter trois fois avancer de 50 pas tourner de 120° sens trigonométrique fin répéter

Question 2 Quelle figure est-elle obtenue avec le bloc principal ?

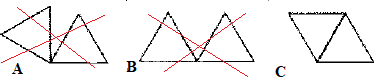3) Quel polygone obtient-on si on remplace dans le script principal, la boucle « répéter 2 fois» par une boucle « répéter 6 fois ?
Un hexagone.
Partie B.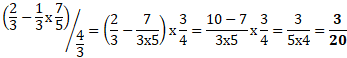

L'écriture scientifique de 302,4 x 10¹⁸ est :3,024 10²⁰.
On donne la masse de 8 biscuit différents : 12 g ; 10 g ; 18 g ; 8 g : 12 g ; 15 g ; 11 g ; 13 g.
Suite à,une erreur de mesure, le biscuit pesant 18 g pèse en fait 16 g.
Une fois cette erreur corrigée, la valeur de la médiane sera :
8 ; 10 ; 11 ; 12 ; 12 ; 13 ; 15 ; 18.
Sans correction la médiane est 12.
8 ; 10 ; 11 ; 12 ; 12 ; 13 ; 15 ; 16.
La médiane est toujours la même : 12.

Exercice 2 (24 points)
Une famille souhaite installer dans son jardin une cabane. La partie inférieure de cette cabaneest modélisée par le schéma :

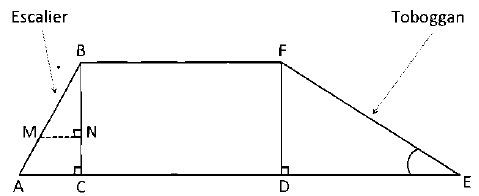
On précise que:
AB = 1,3 m ; DE = 2,04 m ; AC = 0,5 m ; les triangles ABC, BMN et FDE sont rectangles.
BC = DF = 1,2 m.
Partie A: Étude du toboggan
1) Pour que le toboggan soit sécurisé, il faut que l'angle DEF mesure 30°, au degré près.
Le toboggan de cette cabane est-il sécurisé ?
tan (DEF) = DF / DE = BC / DE = 1,2 / 2,04 =0,588 ; l'angle (DEF) mesure 30°. ( donc sécurité).
2) Montrer que la rampe du toboggan, EF, mesure environ 2,37 m.
Théorème de Pythagore : FE² = DF² + DE² =1,2² +2,04² =5,6016 ; EF ~2,37 m.

Partie B : Étude de l'échelle
Pour consolider l'échelle, on souhaite ajouter une poutre supplémentaire [MN], comme indiqué sur le modèle.
1) Démontrer que les droites (AC) et (MN) sont parallèles.
Les droites (AC) et (MN) sont perpendiculaires à la droite (BC) : elles sont donc parallèles.
2) On positionne cette poutre [MN] telle que BN = 0,84 m. Calculer sa longueur MN.
Relation de Thalès : BN / BC = MN / AC = 0,84 / 1,2 = 0,7.
MN = 0,7 AC = 0,7 x0,5 = 0,35 m.

Partie C : Étude du bac à sable
Un bac à sable est installé sous la cabane. Il s'agit d'un pavé droit dont les dimensions sont données cidessous:
Bac à sable
Longueur: 200 cm ; largeur: 180 cm ; hauteur: 20 cm.
1) Calculer le volume de ce bac à sable en cm³.
200 x180 x20 =720 000 cm³.
2) On admet que le volume du bac à sable est de 0,72 m³, On remplit entièrement ce bac avec un mélange de sable à maçonner et de sable fin dans le ratio 3 : 2.
Vérifier que le volume nécessaire de sable à maçonner est de 0,432 m³ et que celui de sable fin est de 0,288 m³.
Sable à maçonner : 0,72 / 5 x 3 =0,432 m³ ;
Sable fin : 0,72 / 5 x 2 =0,288 m³ ;
3) Un magasin propose à l'achat le sable à maçonner et le sable fin, vendus en sac. D'après les indications ci-dessous, quel est le coût total du sable nécessaire pour remplir entièrement ce bac à sable sachant qu'on ne peut acheter que des sacs entiers ?
Sable à maçonner : volume 0,022 m³ par sac ; nombre de sacs :0,432 / 0,022 ~ 20 sacs.
Coût : 20 x2,95 =59 €.
Sable fin : volume 0,016 m³ par sac. 0,288 / 0,016 ~18 sacs.
Coût : 18 x 5,95 =107,1 €.
Total : 59 +107,1 = 166,1 €.

Exercice 3 (15 points)
Amir et Sonia ont chacun inventé un programme de calcul.
Amir : choisir un nombre ; soustraire 5 ; prendre le double du résultat.
Sonia : choisir un nombre ; ajouter 3 ; multiplier le résultat par le nombre choisi ; soustraire 16.
1) Montrer que si le nombre choisi au départ est 6 alors on obtient 2 avec le programme d'Amir et on obtient 38 avec celui de Sonia.
Amir : 6 -5= 1 ; 1 x2 =2.
Sonia : 6+3=9 ; 9 x6 =54 ; 54-16 = 38.
2) Amir et Sonia souhaitent savoir s'il existe des nombres choisis au départ pour lesquels les deux
programmes renvoient le même résultat. Pour cela, ils complètent la feuille de calcul ci-dessous :

Aucune justification n'est attendue pour les deux questions ci-dessous.
a) Parmi les trois propositions suivantes, recopier sur votre copie la formule qui a été saisie dans la
cellule B2 avant d'être étirée vers la droite.
=(B1- 5)*2 vrai ; =(-2 - 5)*2 =B1-5*2
b) En vous aidant de la feuille de calcul, quel nombre doivent-ils choisir pour obtenir des résultats égaux avec les deux programmes?
Nombre 2.
3) Sonia et Amir souhaitent vérifier s'il existe d'autres nombres permettant d'obtenir des résultats
égaux avec les deux programmes.
Pour cela, ils décident d'appeler x le nombre choisi au départ de chacun des programmes.
a) Montrer que le résultat obtenu avec le programme de Sonia est donné par x² + 3x - 16.
(x+3)x-16 =x² + 3x - 16.
b) On admet que les programmes donnent le même résultat si on choisit comme nombre de départ
les solutions de l'équation (x - 2) et (x + 3) =0.
Résoudre cette équation et en déduire les valeurs pour lesquelles les deux programmes de calcul renvoient le même résultat.
x-2 = 0 soit x = 2.
x+3=0 soit x = -3.