Mathématiques, Nlle Calédonie, DNB 2023.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Exercice 1.  QCM (15 points).
1. La probabilité qu'une personne subisse une attaque mortelle de requin au cours de sa vie est de 2,7 10-7. Réponse A.
Une probabilité est comprise entre 0 et 1.
2.
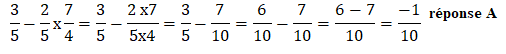3. Un pantalon est vendu 60 € au lieu de 80 €. Le pourcentage de réduction est de :
(80-60) / 80 x100 = 25 % réponse B.
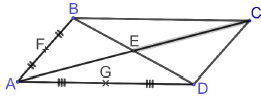
4. ABCD est un parallélogramme de centre E. L'homothétie de centre A qui transforme B en F transforme C en E. Réponse C.

5. La médiane de la série ci-dessous est :
3 ; 5 ; 8 ; 10 ; 11 ; 12 ; 14 ; 17 ; 20. Réponse C.
.
Exercice 2 18 points.
José veut préparer des paniers de légumes pour ses clients. Il a déja récolté 39 salades, 78 carottes et 51 aubergines.
Tous les paniers ont la même composition et tous les légumes seront utilisés.
1.a Décomposer en facteurs premiers les nombres 39, 78 et 51.
39 = 3 x 13.
51=3 x 17.
78= 2 x 3 x 13.
1.b. En déduire le nombre maximum de paniers et la composition de chaque panier.
PGCD de ces trois nombres = 3.
Chaque panier compte 13 salades, 17 aubergines et 26 carottes.
 José décide de préparer 13 paniers.
2.a Combien d'aubergines ne seront pas utilisée ?
51= 13 x 3+12.
Chaque panier contient 3 aubergines et il en restera 12.
2.b. Combien doit-il cueillir d'aubergines supplémentaires  pour pouvoir toutes les utiliser ?
52 = 4 x 13. Il faut cueillir une aubergine supplémentaire.
José souhaite que ses paniers contiennent des tomates. Il estime qu'il y a entre 110 et 125 prêtes à être récoltées. Combien doit-il en récolter pour éviter la perte et pour que chaque panier ait la même composition ?
Rechercher un multiple de 13 compris entre 110 et 125.
13 x 9 =117.

Exercice 3. 18 points.
Mathieu souhaite isoler la toiture de sa maison en utilisant de la laine de roche pour le toit de sa terrasse et de la ouate de cellulose pour le toit de la partie habitable.

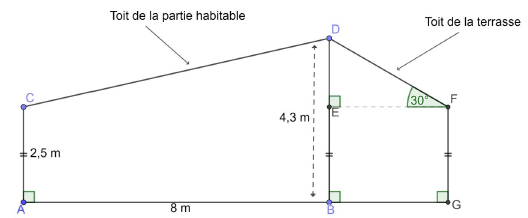1. Justifier que DE = 1,8 m.
DE = BD -BE = BD -AC = 4,3 -2,5 =1,8 m.
2. Montrer que DF = 3,6 m.
sin 30 = DE / DF ; DF = DE / sin 30 = 1,8 / 0,5 = 3,6 m.
Le toit de la terrasse est un rectangle de longueur 12 m et de largeur 3,6 m ; un roukeau de laine de roche couvre 6 m2.
3. Combien de rouleaux faut-il acheter ?
12 x 3,6 / 6 =7,2.
Il faut acheter 8 rouleaux.
4. Montrer que CD = 8,2 m.
Relation de Pythagore dans le triangle rectangle CDE.
CD2 = CE2+DE2 =82+1,82=67,24 ; CD =8,2 m.
Le toit de la partie habitable est un rectangle de longuer 12 m et de largeur 8,2 m. L'épaisseur de la ouate est de 10 cm. La densité de la ouate est 40 kg m-3.
5. Déterminer la masse de ouate à acheter.
Volume de ouate : 12 x 8,2 x 0,10 = 9,84 m3.
Masse de ouate : volume fois densuté = 9,84 x 40 =393,6 kg.

.
.
....

 Exercice 4 13 points

Fabienne parcourt la distance DP en 2 heures.
1.  Justifier que les droites (PN) et (VM) sont parallèles.
Les droites (PN) et (VM) sont perpendiculaires à la droite (DM). Elles sont donc parallèles.
2. Calculer PN.
Relation de Thalès :PN / VM = DP / DV = 3 / 3,8.
PN = 3 / 3,8 x VM = 3 / 3,8 x0,741 =0,585 km.
3. Quelle est la vitesse moyenne de ce parcours ?
3 / 2 = 1,5 km / h.
Sur la partie PV, Fabienne marche à une vitesse de 1,2 km / h. La durée de l'aller simple est estimée à 2 h 30 min.
4. A-t-elle dépassé cette durée ?
Durée du parcours PV : distance / vitesse = 0,8 / 1,2 ~0,67 h ou 40 min.
Durée totale du trajet : 2 h +40 min = 2 h 40 min. Durée dépassée.

Exercice 5. 20 points.

1.a La fonction f est-elle affine?
Non, le graphe n'est pas une droite ne passant pas par l'origine.
1.b Compléter le tableau de valeurs de la fonction f.

 A
 B
 C
 D
 E
 F
 G
1
 x
 -3
 -2
 -1
 0
 1
 2
2
 f(x)
 0
 -3
 -4
 -3
 0
 5

1.c Quelle formule a été saisie en B2 puis étendue dans C2 ?
=(B1+3)*(B1-1).
2. On considère la fonction affine g(x) = 2x+1.
2.a Calculer g(-2).
g(2) = 2 *(-2)+1 = -3.
2.b. Calculer g(3).
g(3) = 2 *3+1 = 7.
2.c. Déterminer l'antécédant de 2 par la fonction g.
2 = 2x+1 ; 2-1 = 2x ; 1 = 2x ; x = 0,5.
2.d. Tracer le graphe de la fonction g.

3. f(x) = (x+3)(x-1).
a. Développer et réduire cette expression.
(x+3)(x-1) = x2-x+3x-3 =x2+2x-3.
b. Pour quelles valeurs de x a-t-on f(x) =g(x)
x2+2x-3 = 2x+1.
x2-3 = 1.
x2 = 4 ; x = ±2.

Exercice 6. (16 points).
Un hexagone régulier est un polygone à 6 côtés de même longueur et dont tous les angles mesurent 120°.
1.a Calculer la mesure de l'angle XBC dans la figure ci-dessous.

180-120=60°.
b. Compléter les deux informations manquantes du bloc Hexagone pour qu'il trace un hexagone régulier.

2. On considère le script suivant.
a. Combien d'hexagones ce script trace t-il ? 5.
b. Quelle est la longueur des côtés du premier hexagone ? 32.
c. Quelle est la longueur des côtés du deuxième hexagone ?
32 x1,5 =48.
d. Quel dessin correspond au script ?

  
menu