CTN, photovoltaïque, oxydo-réduction, mathématiques. Bac Sti2d Métropole 09 / 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Contrôle de la température dans un lave-linge. Lors d’un cycle de lavage d’une machine à laver le linge, la phase qui consomme le plus d’énergie est le chauffage de l’eau utilisée en phase de lavage. Chauffage de l’eau dans le lave-linge. Le chauffage de l’eau est assuré par une résistance chauffante d’une puissance électrique Pélec=2,0 kW. En moyenne, le volume de l’eau utilisée lors d’une phase de lavage est V = 15 L. Q1. Calculer la valeur du transfert thermique Q nécessaire pour chauffer le volume d’eau V𝑉 lors d’un cycle de lavage de 20°C à 40 °C. Q = m ceau (Tfin -Tdébut) =15 x 4180 x(40-20)=1,254 106 J ~1,3 106 J. Q2. Donner la relation entre l’énergie électrique Eélec consommée pendant la durée Dt de la phase de chauffage et la puissance Pélec. Préciser les unités. Pélec = Eélec / Dt. Puissance en watt, énergie en joule et durée en seconde. On considère que toute l’énergie électrique consommée par la résistance chauffante est transférée au volume d’eau. Q3. Vérifier que la durée Dt de la phase de chauffage est de l’ordre de 10 minutes. Dt =Eélec / Pélec =1,254 106 / 2000 =627 s ou environ 10 minutes. Étude d’une thermistance CTN. La température de l’eau est contrôlée par une thermistance CTN, qui est un composant dont la valeur de la résistance électrique R varie en fonction de la température. Il est possible, au laboratoire, d’étudier les variations de la résistance d’une thermistance CTN en fonction de la température à l’aide du montage suivant. 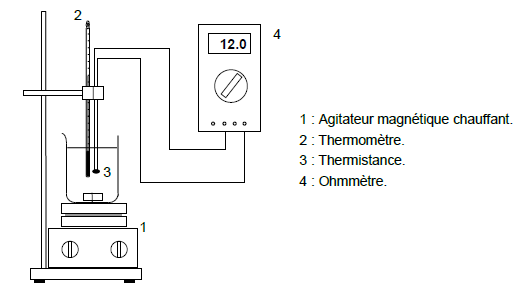Cette résistance (en ohm), en fonction de la température T (en °C), peut être modélisée par la fonction R définie sur [0 ; 100] : R(T)=28785 × e−0,042×T. Q4. À l’aide du graphique, déterminer à partir de quelle température la résistance devient inférieure à 10 kW. 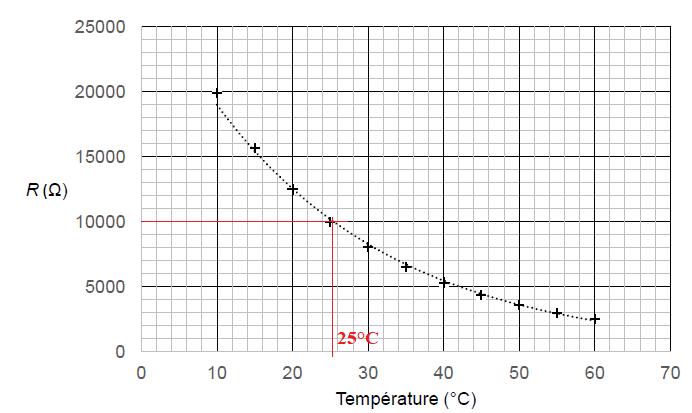Q5. Résoudre sur [0 ; 100] l’équation R(T))=10 000. Comparer avec la valeur lue sur le graphique à la question Q4. 10 000=28785 × e−0,042×T. e−0,042×T =10000 / 28785 =0,347. -0,042T = ln(0,347) =-1,057. T =1,057 / 0,042 ~25°C. Q6. On note R' la fonction dérivée de R sur [0 ; 100]. Déterminer une expression de R'(T) . R'(T) = 28785 x(-0,042 )e−0,042×T = -1,21 103 e−0,042×T. La sensibilité de la thermistance CTN est donnée par la fonction S définie sur [0 ; 100] par : S= -dR / dT. Le dispositif de régulation de la température sera d’autant plus performant que la valeur de la sensibilité de la thermistance sera grande. Q7. Montrer que la sensibilité de la thermistance CTN est environ 12 fois plus grande à 30°C qu’à 90°C. A 30°C : S =1,21 103 e−0,042×30=343. A 90°C : S =1,21 103 e−0,042×90~28 soit environ 343 /12. Alimentation d’un moteur par un panneau photovoltaïque. On désire alimenter une pompe de piscine à l’aide d’un panneau photovoltaïque. On réalise pour cela une maquette miniaturisée constituée d’un panneau photovoltaïque, d’un moteur et d’une batterie. Étude du panneau photovoltaïque. Q1. Indiquer quelles sont les formes d’énergie mises en jeu dans la conversion photovoltaïque. L'énergie solaire est convertie en énergie électrique et en énergie thermique. On donne la courbe représentant la puissance électrique P fournie par le panneau en fonction de la tension à ses bornes, notée U : 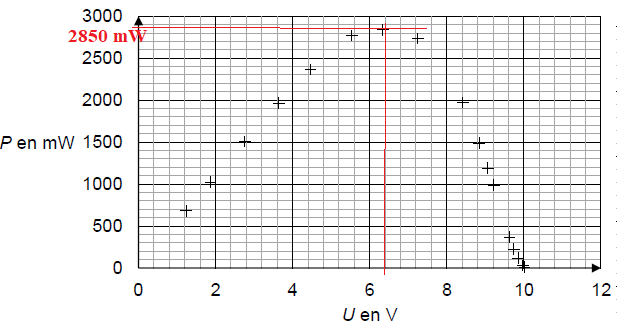Q2. Sachant que les mesures ont été effectuées avec une irradiance qui vaut 1100 W m-2 et que l’aire du panneau photovoltaïque est S = 6,4 × 10-2 m2, montrer que le rendement maximal du panneau photovoltaïque vaut environ 4 %. Puissance solaire : 1100 x6,4 10-2 =70,4 W. Rendement maximum = puissance électrique / puissance solaire x100 =2,85 /70,4 x100~4,0 %. Choix d’un moteur. On souhaite alimenter un moteur avec le panneau photovoltaïque étudié précédemment. Pour choisir le moteur adéquat, on réalise le montage suivant permettant de tracer la courbe représentant l’intensité en fonction de la tension d’un moteur. 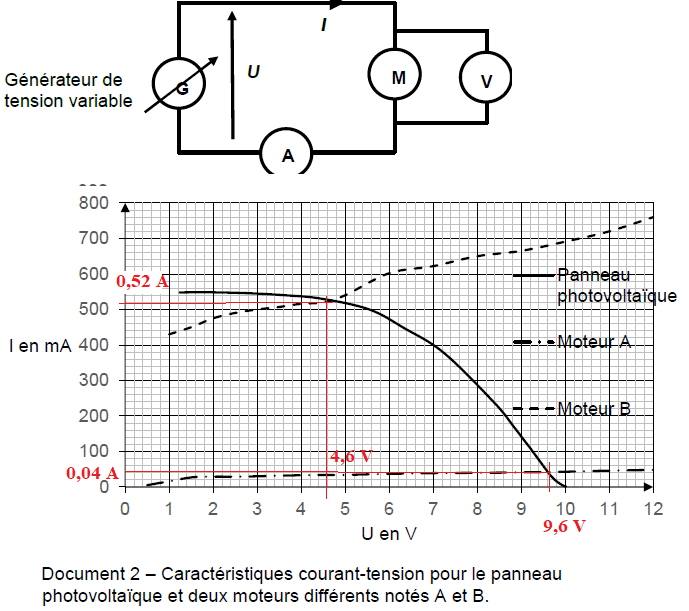Q3. Préciser les coordonnées (tension et intensité) des points de fonctionnement des moteurs A et B connectés au panneau photovoltaïque. Q4. Choisir, parmi les moteurs A et B, celui qui permet de se rapprocher le plus du rendement maximal du panneau photovoltaïque. Justifier. Moteur A : 9,6 x0,04 =3,84 , supérieur à la puissance électrique maximale fournie par le panneau. Moteur B : 4,6 x0,52 = 2,4 W inférieure et plus proche de 2,85 W, puissance électrique maximale fournie par le panneau. Étude de l’accumulateur. On souhaite brancher le panneau photovoltaïque à un accumulateur permettant d’utiliser le moteur même en l’absence de soleil. Tension : 6,0 V ; capacité : 3000 mA h ; énergie massique : 50 W h kg-1. Q5. Le panneau photovoltaïque charge l’accumulateur avec une intensité Icharge = 480 mA et un rendement de conversion d’énergie électrique en énergie chimique h = 80 %. Calculer le temps de charge de l’accumulateur. Puissance électrique fournie par le panneau : 6,0 x 0,48 x0,80=2,3 W. Durée de la charge : 50 / 2,3 ~9,5 h kg-1. Durant sa décharge, un l’accumulateur Ni-MH est le siège de demi-équations d’oxydoréduction mettant en jeu les couples suivants : - À la borne positive : NiO(OH) / Ni(OH)2 - À la borne négative : M / MH où M désigne un métal non spécifié et MH un hydrure de ce métal. Q6. Parmi les propositions suivantes, indiquer sur la copie celle qui correspond à la demi-équation de réduction ayant lieu à la borne positive pendant la décharge : A. NiO(OH) + H2O + e- = Ni(OH)2 + HO-. Vrai. B. Ni(OH)2 = NiO(OH) + H+ + e-. C. MH + HO- = M + H2O + e-. D. M + H+ + e- = MH. Lors d'une réduction l'oxydant gagne un ou plusieurs électrons. Q7. Parmi les valeurs d’énergies suivantes, indiquer sur la copie celle qui correspond à l’énergie disponible dans l’accumulateur. A. 2,0 Wh B. 65 kJ ou 65 /3,6=18 Wh. C. 7,2 kJ D. 18 000 J. Capacité  fois tension = 3,0 x 6 = 18 Wh. Q8. L’énergie massique est l’énergie que peut stocker l’accumulateur par unité de masse d’accumulateur. Calculer la masse de la batterie. 18 / 50=0,36 kg. Q9. On désire faire fonctionner le moteur B, dont la caractéristique courant-tension est donnée de nuit, en le connectant à l’accumulateur considéré. Calculer la durée maximale de fonctionnement avec un rendement de conversion de 75 %. On supposera que l’accumulateur est un générateur de tension idéal qui fournit une tension de 6,0 V quelle que soit l’intensité débitée. Energie électrique fournie au moteur : 18 x0,75=13,5 Wh. Tension  aux bornes du moteur : 6 V ; intensité correspondante =0,6 A d'après le graphe. Durée de fonctionnement : 13,5 / (6 x0,6) =3,4 h. ... .... Mathématiques. Question 1. On considère un réel 𝑥, strictement positif et on note log (𝑥)= ln (𝑥)/ ln (10). Pour tout réel 𝑥, strictement positif, log(100𝑥) est égal à : log (100 x) = log (100) + log(x) =2+log(x). Réponse C. Question 2 On considère la fonction f définie sur ℝ par f(x)= 2e3𝑥−2. Déterminer la limite de la fonction f en −oo. En moins l'infini e3x tend vers zéro et f(x) tend vers -2. Question 3 On désigne par i le nombre complexe de module 1 et d’argument p/2. Le plan est muni d’un repère orthonormé (O ; u ; v ). Sur le graphique suivant, on considère le point E dont l’affixe est notée : zE. 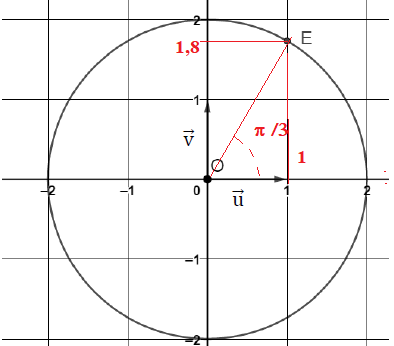Par lecture graphique, donner l’écriture exponentielle de zE. zE = 2 exp ( i p / 3). Question 4 On considère l’équation différentielle (E) : y′=2y+0,5 , où y est une fonction de la variable x, définie et dérivable sur R et y' la fonction dérivée de y. Déterminer les solutions sur R de l'équation différentielle (E). Solution générale de y' -2y = 0 : y = A exp(2x) avec A une constante réelle. Solution particulière de (E) : y = -0,25. Solution générale de (E) : y = A exp(2x) -0,25. Étude d’un défaut sur un roulement à billes. Au cours du temps, les différentes frictions s’exerçant sur le roulement réduisent la quantité de graisse présente entre les bagues qui le constituent. Les parties métalliques en fer s’oxydent alors progressivement au contact de l’air. A l'air libre les deux couples oxydant-réducteur mis en jeu sont les suivants : Fe2O3(aq) / Fe(s) O2(g) / H2O (l) Q1. D’après l’énoncé et les couples mis en jeu, déterminer les réactifs qui sont impliqués dans la corrosion du fer. Fe(s) et O2(g) Q2. Écrire la demi-équation d’oxydoréduction correspondant au couple O2(g) / H2O (aq). O2(g) +4H+ aq + 4e---> 2H2O (aq). Q3. Sachant que la demi-équation correspondant au couple Fe2O3(aq) / Fe(s) est la suivante : 2Fe(s) + 3H2O(l) = Fe2O3(s) + 6H+(aq) + 6e-. Montrer que l’équation modélisant la transformation s’écrit : 3O2(g) + 4Fe(s) → 2Fe2O3(s). 4Fe(s) + 6H2O(l) =2 Fe2O3(s) + 12H+(aq) + 12e-. 3O2(g) +12H+ aq + 12e---> 6H2O (aq). Ajouter puis simplifier. 4Fe(s) + 6H2O(l) +3O2(g) +12H+ aq + 12e-=2 Fe2O3(s) + 12H+(aq) + 12e-+6H2O (aq). Q4. Expliquer pourquoi les roulements à billes initialement graissés ne s’oxydent pas. Le fer n'est pas en contact avec le dioxygène de l'air. Perte d’efficacité d’un roulement corrodé Les roulements à billes permettent de diminuer les frottements qui peuvent s’exercer entre l’axe et la roue. Afin d’évaluer la perte d’efficacité d’un roulement oxydé, deux chronophotographies du mouvement d’un véhicule  sont réalisées. Pour la première chronophotographie, le véhicule est équipé de roulements neufs alors que pour la seconde les roulements utilisés sont légèrement oxydés. Le véhicule, de masse m = 1,2 kg est lancé avec une vitesse initiale V0 = 1,1 m.s-1 sur une surface horizontale. La chronophotographie permet d’obtenir les positions en fonction du temps. 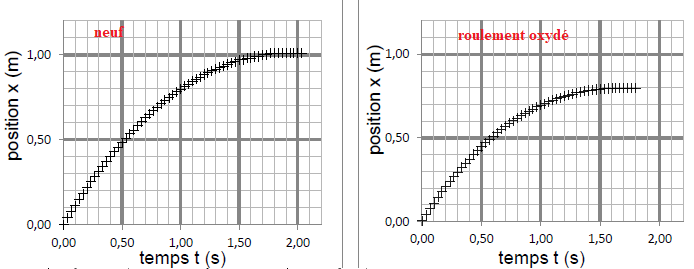Q5. À l’aide des graphiques, discuter de l’efficacité des roulements en présence d’oxydation. Roulement neuf : au bout de 1,5 s, la distance parcourue est d'environ 1 m. Roulement oxydé : au bout de 1,5 s, la distance parcourue est d'environ0,8 m. les frottements sont beaucoup plus importants. On assimile l’ensemble des frottements qui s’exercent sur le véhicule à une seule force s’opposant au mouvement, notée f , considérée constante. Dans le cas de roulements à billes neufs, cette force de frottements a pour valeur f = 0,72 N. Le véhicule est également soumis à deux autres forces : le poids P et la réaction du support R , représentées sur le schéma ci-dessous. Q6. Rappeler l’expression du travail d’une force F sur l’ensemble du trajet correspondant au vecteur déplacement AB . En déduire la valeur du travail des forces P et R sur l’ensemble du trajet. 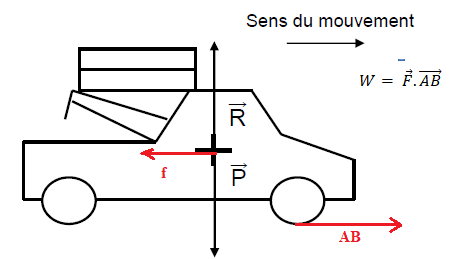Les forces P et R, perpendiculaires au déplacement ne travaillent pas. On note f la force, considérée constante et s’opposant au mouvement lorsque les roulements à billes sont oxydés. Q7. Montrer que le travail W ’ de la force de frottement f sur l’ensemble du trajet est donné par W '= −f d. Les vecteurs forces de frottement et déplacement sont colinéaires et de sens contraire. Q8. À l’aide des graphiques précédents, déterminer la distance totale d parcourue par la voiture possédant les roulements oxydés jusqu’à son arrêt. Justifier le raisonnement. Quand x devient constant ( 0,8 m) la voiture est à l'arrêt. Q9. Déterminer la valeur du travail W ’ et en déduire que la force de frottements, dans le cas de roulements oxydés, a pour valeur f ’ = 0,9 N. Commenter. Théorème de l'énergie cinétique : 0 -½mv02 = W ' = -f AB = -0,8 f. 0,5 x1,2 x1,12 = 0,8 f ; f = 0,9 N.

menu