De la pomme au calvados en passant par le cidre, bac SPCL Polynésie 2023.

Partie 1 : du jus de pomme au calvados (10 points)
Détermination du type de cidre : Les sucres du moût.
La fabrication du cidre commence par le broyage et le pressurage de pommes permettant d’obtenir un jus appelé moût. Ce moût contient une forte quantité de sucres dont les deux principaux sont le glucose et le fructose. La concentration en masse totale de sucre dans ce jus est de 107 g·L^–1 . Les molécules de glucose et de fructose Leur formule brute est identique : C₆H₁₂O₆.
1.1. Entourer les groupes caractéristiques présents dans la molécule de glucose et donner les noms des fonctions chimiques correspondantes.

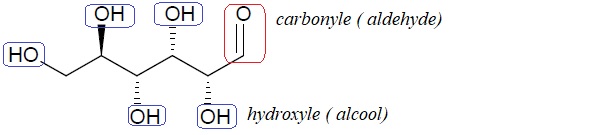1.2. Citer un réactif utilisé pour identifier le groupe fonctionnel -CHO du glucose.
Réactif de Benedict et liqueur de Fehling.
L’éthanol formé par fermentation.
Le jus de pomme subit la fermentation alcoolique qui conduit à la formation d’éthanol de formule brute C₂H₆O et de dioxyde de carbone. Il existe différents types de cidre en fonction de la teneur en sucre. Pour déterminer le caractère brut, demi-sec ou doux du cidre, on réalise un dosage indirect de l’éthanol qu’il contient. On désigne par C₀ la concentration en quantité de matière en éthanol dans le cidre.
Étape 1 : oxydation de l’éthanol par les ions permanganate en milieu acide.
Dans un erlenmeyer : - Introduire un volume V₀ = 10,0 mL de cidre. - Ajouter un volume V₁ = 150,0 mL d’une solution acidifiée de permanganate de potassium (K⁺ (aq) +MnO₄ ⁻(aq)) de concentration en quantité de matière C₁ = 5,00×10^-2 mol∙L^-1 . Les ions permanganate et les ions H⁺ sont ainsi introduits en excès. - Laisser le temps nécessaire à la transformation de s’effectuer.
L’équation de la réaction s’écrit : 5 C₂H₆O(aq) + 4 MnO₄ ⁻(aq) + 12 H ⁺(aq) → 5 C₂H₄O₂ (aq) + 4 Mn²⁺(aq) + 11 H₂O(l)
Étape 2 : dosage des ions permanganate en excès.
On réalise ensuite le dosage des ions permanganate restants par une solution contenant des ions Fe²⁺ à la concentration en quantité de matière C₂ = 7,00×10^-1 mol∙L^-1 .
Données : Couples oxydant-réducteur mis en jeu lors du dosage de l’étape 2 : MnO₄ ⁻ / Mn²⁺ et Fe³⁺ / Fe²⁺ .
1.3. Montrer que l’équation de la réaction support du titrage entre les ions permanganate et les ions Fe²⁺ de l’étape 2 est :
MnO₄ ⁻(aq) + 5 Fe²⁺(aq) + 8 H⁺(aq) --> Mn²⁺(aq) + 5 Fe³⁺(aq) + 4 H₂O(l).
MnO₄ ⁻(aq) +5e^- + 8 H⁺(aq)--> Mn²⁺(aq) + 4 H₂O(l).
5 Fe²⁺aq --> 5 Fe³⁺ aq + 5e^-.
Ajouter et simplifier.

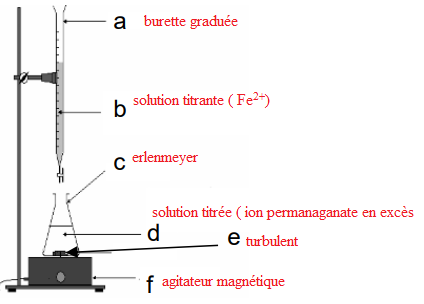
Le schéma du dispositif de titrage est donné ci-dessous.
1.4. Sur la copie, associer les lettres a, b, c, d, e et f, au nom du matériel et des solutions correspondantes.

Le volume de solution aqueuse d’ions Fe²⁺ versé à l’équivalence vaut V_E = 13,8 mL. On fera l’approximation que la seule espèce colorée en solution est l’ion permanganate.
1.5. Indiquer comment on repère précisément l’équivalence de ce titrage.
Avant l'équivalence, l'ion permanganate est en défaut, solution incolore.
Après l'équivalence, l'ion permanganate est en excès, solution violette.
1.6. Définir l’équivalence d’un titrage.
A l'équivalence, les quantités de matière des réactifs sont en proportions stoechiométriques.
1.7. Montrer que la quantité de matière d’ions permanganate restante à la fin de l’étape 1 vaut n(MnO₄ ⁻)_{𝑟𝑒𝑠𝑡𝑎𝑛𝑡}= 1,93×10^-3 mol.
n(Fe²⁺) =C₂VE = 0,700 x 13,8 =9,66 mmol.
n(MnO₄ ⁻)_{𝑟𝑒𝑠𝑡𝑎𝑛𝑡}=n(Fe²⁺) / 5 =9,66 / 5 =1,93 mmol.
On en déduit que la quantité de matière d’éthanol contenue dans l’échantillon de cidre de volume V₀ = 10,0 mL vaut n₀ = 6,96∙10^-3 mol.
1.8. Calculer la concentration C₀ en quantité de matière en éthanol dans le cidre analysé.
C₀ = n₀ / V₀ = 6,96 10^-3 / (10 10^-3)=0,696 mol / L.
1.9. 1.10 En déduire la concentration en masse Cm de l’éthanol dans le cidre sachant que la masse molaire de l’éthanol est M= 46,0 g∙moL^{– 1} .. Montrer que la masse d’éthanol présente dans 100 mL de ce cidre vaut 3,20 g.
0,696 x46 = 32,0 g / L soit 3,20 g dans 100 mL.
Le degré alcoolique d’un cidre (exprimé en % volumique) correspond au volume d’éthanol (en mL) contenu dans 100 mL de cidre. On donne la masse volumique de l’éthanol : µ = 0,79 g∙mL^{– 1}
1.11. Déterminer le degré alcoolique d du cidre étudié.
Volume d'éthanol = 3,20 / 0,79 = 4,05 mL dans 100 mL de cidre soit 4,05 degrés.
Le cidre est demi-sec.
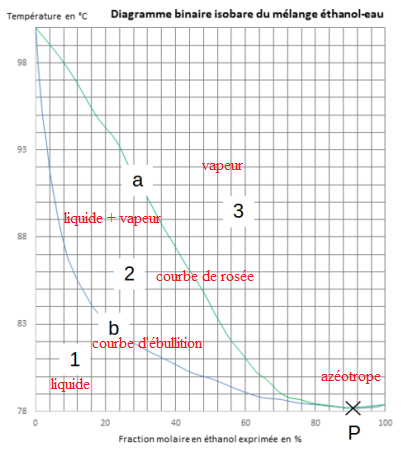
Le calvados est une boisson alcoolisée traditionnelle obtenue par distillation du cidre. La mise au point du procédé de distillation exploite le diagramme binaire isobare du mélange éthanol / eau fourni.
1.13. Nommer : - les phases correspondant aux trois domaines numérotés 1, 2 et 3.
- les deux courbes (a) et (b) délimitant les trois domaines. - le point P.

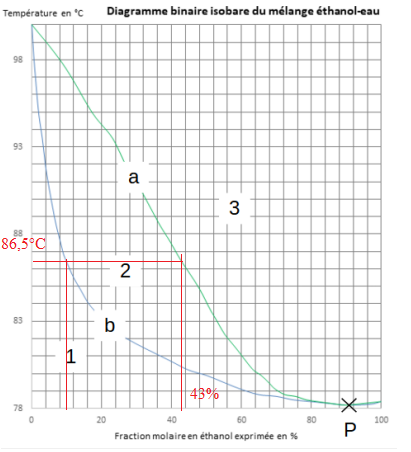
En première approximation, le distillat obtenu après une première distillation peut être assimilé à un mélange eau-éthanol de fraction molaire en éthanol de 10 %, qui est engagé dans une deuxième distillation.
1.14. Déterminer, en faisant les constructions nécessaires : - la température d’ébullition de ce mélange. - la fraction molaire en éthanol des premières bulles de vapeur.

1.15. Préciser, en justifiant, s’il est possible d’obtenir de l’éthanol pur par plusieurs distillations successives.
Non, on obtient l'azéotrope P.
Première approche d’une boucle de régulation de température dans un procédé de distillation industrielle.
Dans le procédé de distillation industrielle, il est nécessaire de contrôler la température du distillat en sortie du condenseur en agissant sur le débit d’eau froide, afin de limiter l’influence de la température extérieure et des variations de débit des vapeurs d’alcool. On dispose du matériel suivant :
Un capteur-conditionneur de température permettant la conversion d’une température mesurée en une tension,
Un régulateur qui compare la consigne de température à la température mesurée et ainsi commande une électrovanne,
Une électrovanne qui permet de laisser passer (électrovanne ouverte) ou d'arrêter (électrovanne fermée) l’eau froide,
Un échangeur thermique permettant la double circulation à contre-courant des vapeurs d’alcool et du fluide frigorigène.
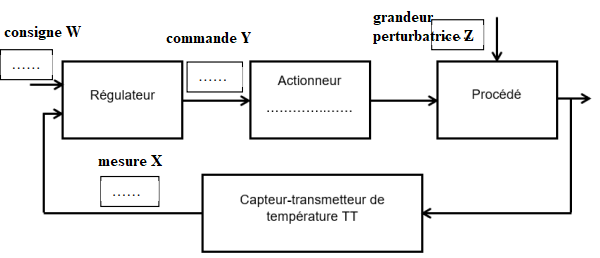
1.16. Indiquer la grandeur réglée, la grandeur réglante et une grandeur perturbatrice.
Grandeur réglée : température du distillat.
Grandeur réglante : débit d'eau froide.
Grandeur perturbatrice : la température extérieure et les variations de débit des vapeurs d’alcool.
1.17. Compléter le schéma de la boucle de régulation en légendant les blocs.

Le régulateur est constitué d’un microcontrôleur dont une partie du programme est donnée ci-après. L’électrovanne est ouverte (laissant passer l’eau froide) lorsque la sortie de la carte microcontrôleur est à l’état haut (HIGH). L’électrovanne est fermée (ne laissant pas passer l’eau froide) lorsque la sortie de la carte microcontrôleur est à l’état bas (LOW).
1.18. Recopier et compléter les lignes 15 et 19 avec les termes HIGH et LOW.

Partie 2 : mesure de la concentration de sucre par polarimétrie (3 points)
Une des techniques envisagées pour mesurer la concentration en sucre dans le moût est la polarimétrie.
2.1. Préciser la caractéristique principale de la source de lumière du polarimètre de Laurent.
LUmière monochromatique l = 589,44 nm
Lorsque la cuve contient de l’eau distillée et que les axes des polariseurs P₁ et P₂ sont perpendiculaires, on n’observe aucune lumière sur l'écran (extinction totale). On remplace l’eau distillée par une solution de glucose de concentration en masse C_m dans la cuve (ou tube) de longueur ℓ = 20,00 cm placée entre P₁ et P₂, sans modifier les positions des axes.
2.2. Justifier le fait que l'écran est à nouveau éclairé.
L'intensité de la lumière sera maximale si les axes des polariseurs sont les mêmes et sera nulle s'ils sont perpendiculaires. Si on introduit une substance optiquement active dans la cuve, l'intensité de la lumière n'est pas nulle ou maximale; pour retrouver une intensité nulle ou maximale, il faudra tourner le prisme analyseur d'un angle a.
Pour obtenir à nouveau l'extinction totale, on doit tourner l’axe D₂ d’un angle a= 11,00 ° vers la droite, ceci en regardant la source. On désigne par [a₀] le pouvoir rotatoire spécifique du sucre utilisé. Donnée : [a₀]glucose = 5,2 °∙g^–1 ∙cm².
2.3. En exploitant la loi de Biot, montrer que la valeur de la concentration en masse C_m de la solution de glucose vaut 106 g/L
a = [a₀] l Cm.
Cm = 11 / (5,2 x20)=0,106 g / cm³ = 106 g / L.
2.4. Identifier deux sources d’erreur lors de la détermination de la concentration en masse 𝐶m.
Mesure de a et longueur de la cuve..
On s’intéresse maintenant à la qualité de la mesure de la concentration en masse Cm. On peut estimer l’incertitude-type sur la mesure de Cm à l’aide de la relation suivante :
u(Cm) = 𝐶m × [(( u(l)/ l ) ² + ( u([a₀]) / [a₀] ) ² + ( u(a)/ a )² ]^½.
l’incertitude-type sur la longueur de la cuve vaut u(l) = 0,04 cm, l’incertitude-type sur le pouvoir rotatoire mesuré vaut u(a) = 0,02°, on négligera l’incertitude-type sur le pouvoir rotatoire spécifique du glucose par rapport aux autres incertitudes-types à prendre en compte.
2.5. Calculer l’incertitude-type u(Cm) sur la concentration en masse Cm de la solution de glucose.
u(Cm) = 106 × [(0,04/20 ) ² + ( 0,02 / 11 )² ]^½ =0,286 ~0,3 g / L
2.6. Exprimer le résultat de la mesure de la concentration en masse 𝐶m accompagnée de son incertitude-type associée.
Cm = 106 ±0,3 g / L.

Partie 3 : mesure de la concentration en sucre dans un moût par réfractométrie (4 points).
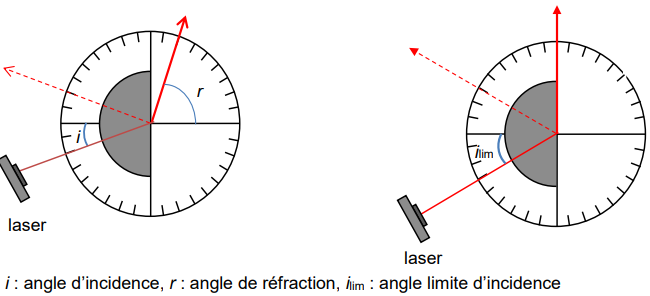
Principe d’une mesure réfractométrique : On place la solution à analyser d’indice de réfraction n₁ dans la cuve hémicylindrique (en gris sur le schéma ci-après). On s’intéresse au passage du rayon lumineux de la solution d’indice n₁ à l’air d’indice de réfraction n₂ = 1 au niveau de la face plane. On augmente l’angle d’incidence i jusqu’à ce que le rayon réfracté disparaisse. On mesure alors l’angle limite i_lim d’incidence correspondant.

3.1. Énoncer la deuxième loi de Snell-Descartes pour la réfraction, en utilisant les données de l’énoncé.
n₁ sin i = n₂ sin r.
3.2. Expliquer ce que devient le rayon lumineux lorsque l’angle d’incidence est supérieur à l’angle limite et nommer le phénomène observé.
Réfrection totale : le rayon réfracté disparaît ; seul existe le rayon réfléchi..
3.3. Montrer que dans la situation de l’angle limite, on peut écrire n₁ = 1/ sin(i_lim).
n₁ sin i_lim = n₂ sin 90 = 1.
3.4. En déduire la valeur de l’indice de réfraction d’un jus de pomme si l’angle limite est i_lim= 47°.
n₁ = 1 / sin(47)=1,37.
On utilise maintenant un réfractomètre professionnel. On utilise ce réfractomètre professionnel pour mesurer l’indice de réfraction d’une gamme de solutions de sucre (tous sucres confondus). Les résultats sont rassemblés dans le tableau ci-après.

solution	eau	S1	S2	S3	S4
concentration en masse( g/L)	0	50,0	100,0	200,0	400,0
indice de réfraction	1,333	1,340	1,347	1,366	1,386

On trace la courbe d’étalonnage représentant l’indice de réfraction n de la solution de sucre en fonction de la concentration en masse de sucre C.

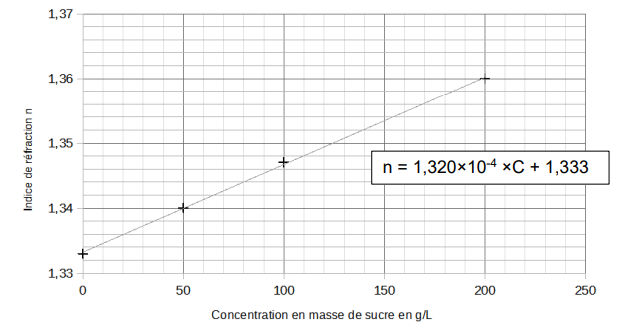
On mesure l’indice de réfraction du moût. Le réfractomètre indique n = 1,348.
3.5. Déterminer sa concentration en masse de sucre.
C = (n-1,333) / (1,320 10^-4)=(1,348-1,333) / (1,320 10^-4)=113,6 g / L.
Il existe une relation de proportionnalité entre la concentration en masse de sucre et le degré d’alcool : une concentration de 17 g∙L^–1 de sucre dans un moût permet d’obtenir 1° d’alcool à la fin du processus.
3.6. Calculer le degré d’alcool maximal qu’il est possible d’obtenir à partir du moût de ce jus si tout le sucre était transformé en alcool.
113,6 / 17 =6,68 ~6,7 °.