Pesée
d'un corps céleste, installation d'une fenètre de toit,
bac STL La Réunion
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| .. |
.
.
|
|
.
.
|
..
..
......
...
|
EXERCICE
A - Peser un corps céleste
(10 points)
Pour déterminer la masse m d’un objet sur Terre, il suffit simplement
de poser cet objet sur
une balance adaptée. Pour les masses d’objets célestes tels que la
Terre elle-même, la
résolution du problème n’est pas aussi simple et directe.
L’objectif de cet exercice est de déterminer expérimentalement la masse
de la Terre notée M.
1. Pour un objet de
masse m situé à la surface de la Terre, rappeler la relation
vectorielle
entre son poids et le champ de pesanteur terrestre.
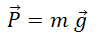
2. En s’appuyant
sur le modèle de la chute libre et une loi de Newton, justifier que
l’intensité
du champ de pesanteur g s’exprime en m·s-2.
Un objet en chute libre n'est soumis qu'à son poids. La seconde loi de
Newton conduit à mg = ma ; g a la dimension d'une accéllération
exprimée en m s-2.
Pour mesurer expérimentalement la valeur de g en un point donné de la
Terre, on peut
utiliser un pendule simple qui oscille périodiquement avec une période
T supposée
constante durant l’expérience .
Pour un pendule de longueur L, on peut montrer que, pour des
angles petits, la période
d’oscillation T s’exprime par la relation : T = 2p ( L /g)½.
Au niveau de l’équateur, pour une longueur de pendule L = 0,991
m, la période est de T = 2,00 s.
3. Déterminer la
valeur de g au niveau de l’équateur.
g = 4 p2
L / T2 =4 x3,142 x0,991 / 4,00 =9,78 m s-2.
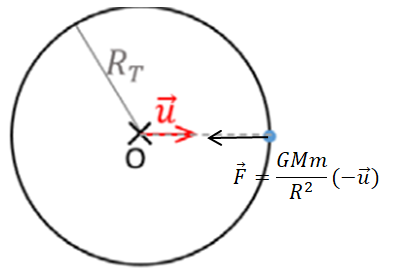
4. Reproduire sur
sa copie le schéma de la Terre ci-dessous et le compléter, sans souci
d’échelle, en rajoutant la force gravitationnelle F exercée par la
planète Terre sur un
corps modélisé par un point matériel de masse m situé à sa surface. Le
vecteur u est un
vecteur unitaire.
Constante de gravitation universelle : G = 6,674 30 × 10-11
N·m2·
kg-2.
Rayon de la Terre au niveau de l’équateur : R = 6 378 km.
5. Exprimer
vectoriellement la force gravitationnelle F exercée par la Terre sur un
objet de
masse m situé à sa surface. En admettant que le champ de gravitation
est égal au champ
de pesanteur et donc que F = P, en déduire l’expression littérale de M
puis calculer sa
valeur numérique.
m g=GMm / R2 ; M =gR2 / G =9,81 x (6378 103)2
/ (6,677430 10-11)=5,97 1024 kg.
Données : Incertitude-type de l’intensité du champ de pesanteur
terrestre : u(g) = 0,05 m·s-2.
Incertitude-type du rayon de la Terre : u(R) = 1 km.
On admettra que : u(M) = M[(u(g) / g)2 +(2 xu(R) / R)2
]½ .
Masse de référence de la Terre : Mréf = 5,98 × 1024
kg ;
6. Calculer
l’incertitude u(M) sur la masse de la Terre et vérifier que la valeur
expérimentale est bien en accord avec la valeur communément
admise de nos jours.
u(M) = 5,98 1024[(0,05 / 9,81)2
+(2 / 6378)2 ]½ = 3,0 1022 kg.
|M-Mréf| / u(M)=(5,98 -5,97) 1024 / (3,0 1022)=0,3
< 2.
Donc accord entre les deux valeurs.
|
...
|
....
|
Installation d'une fenètre de toit.
Afin d’accroître la
luminosité d’une pièce située sous le toit
de sa maison, une famille envisage d’installer une fenêtre
de toiture d’entrée de gamme constituée d’un simple
vitrage de surface S = 1,0 m2.
L’objectif de cet exercice est d’étudier une des
conséquences de cet achat en termes de température lors
de la période estivale.
Pour simplifier, on suppose qu’en période estivale, à partir de midi,
la température de l’air
au voisinage de cette fenêtre est constante et égale qe = 50 °C.
On admettra que la partie toiture en tuiles est parfaitement isolée
thermiquement et que tout
transfert thermique par rayonnement à travers la fenêtre de toit est
négligeable.
On considèrera que le seul transfert thermique échangé par l’air de la
pièce est dû au
transfert conducto-convectif provenant de la vitre.
Coefficient de transfert conducto-convectif : h = 8,0 W·K-1·m-2 ;
Masse d’air contenue dans la pièce : mair = 1,3 × 102 kg ;
Capacité thermique massique de l’air sec : cair = 1,0 × 103 J·K-1·kg-1.
Le flux thermique F(t) entre un système à la température uniforme q(t) et un milieu
extérieur à la température qe fixe (thermostat) peut être modélisé par la loi de Newton : F(t) = h × S × (qe – q(t))
avec F en W ; h coefficient conducto-convectif en W⋅m-2⋅K-1 et S surface d’échange
entre le système et le milieu extérieur, en m2.
1. Exprimer le transfert thermique Q qui a lieu à travers la vitre pendant la durée très courte Dt en fonction de Dt, h, S, qe et q.
Q = F(t) Dt= h × S × (qe – q(t)) Dt.
Le système étudié est l’air de la pièce que l’on considérera incompressible.
2. Appliquer le premier principe de la thermodynamique au système et en déduire une
relation entre F(t) et les grandeurs Dt, mair, cair et Dq où Dq désigne la variation de
température du système pendant la durée Dt.
DU = Q + W avec W = 0.
Q = mair cairDq = h × S × (qe – q(t)) Dt.
3. Montrer que la température de l’air de la pièce q(t) obéit à l’équation différentielle :
dq
/dt
+ a × q(t) = a × qe avec a = h × S
/(mair × cair).
mair cairdq = h × S × (qe – q(t)) dt.
dq / dt=h × S / (mair × cair) (qe – q(t)).
dq / dt=a (qe – q(t)).
dq
/dt
+ a × q(t) = a × qe .
4. En utilisant les données, montrer que a = 6,2 × 10-5 s-1 environ. Justifier son unité.
h × S
/(mair × cair)= 8,0 x1,0 / (1,3 102 x1,0 103)=6,2 × 10-5 s-1 .
a × q(t) doit être homogène à dθ
/dt ; a possède la dimension de 1 / dt, donc s-1.
On admet que la solution à l’équation différentielle a pour expression :
q(t) = qi+(qe-qi)(1-e-at).
où qi est la température de l’air de la pièce à l’instant initial.
5. Calculer la température q de la pièce au bout d’une heure puis au bout de trois heures
lorsque la température initiale intérieure vaut 20 °C. À partir de ces résultats
numériques, justifier si la fenêtre de toit choisie convient lors de la période estivale.
q(3600)=20 +(50-20) (1-exp(-6,2 10-5 x3600))=26 °C.
q(3x 3600)=20 +(50-20) (1-exp(-6,2 10-5 x3 x3600))=35 °C.
La fenètre ne convient pas, n'étant pas suffisamment isolante thermique.
|
|