Le
bateau Energy Observer,
bac STL La Réunion
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| .. |
.
.
|
|
.
.
|
..
..
......
...
|
Energy Observer est à l’origine le nom du premier bateau navigant grâce aux
énergies renouvelables et à l’hydrogène.
Exercice 1. 4 points.
À bord du bateau Energy Observer, l'équipage doit évidemment se nourrir. Plutôt que
d'utiliser du saccharose pour les apports glucidiques, du sirop de sucre inverti a été
embarqué sur le bateau.
Le sucre inverti est un mélange équimolaire de glucose et de fructose issu de
l'hydrolyse du saccharose. Il présente un pouvoir sucrant supérieur d’environ 20 % à
celui du saccharose, ce qui limite la masse embarquée sur le bateau. Il permet
également de réduire le temps de cuisson, donc l'énergie utilisée à bord pour se
nourrir.
La production de sucre inverti est réalisée en laboratoire lors de la transformation
chimique du saccharose en milieu acide, en chauffant.
On définit la vitesse v de disparition du saccharose de concentration c en quantité de
matière par : v = −
dc
dt
Expérimentalement, nous réalisons un suivi cinétique de cette transformation qui
permet d’obtenir le graphe ci-après représentant l’évolution de la vitesse v de
disparition du saccharose en fonction de sa concentration c en quantité de matière
dans le mélange. On peut modéliser cette situation par une fonction linéaire.
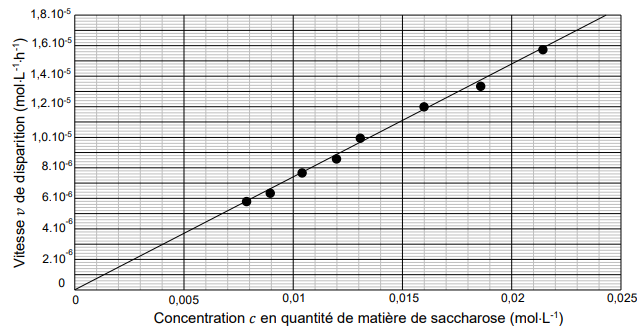
1. À partir du graphique précédent, choisir, en justifiant la réponse, le modèle
adapté à la cinétique chimique de cette réaction parmi les propositions
suivantes :
modèle 1 ∶ v = k ; modèle 2 ∶ v=k c ; modèle 3 ∶ v=kc2
où k est la constante de vitesse.
La droite passe par l'origine, donc fonction linéaire v = k c.
2. Déterminer une valeur approchée de la constante de vitesse k en précisant son
unité.
k =1,1 10-5 / 0,015=7,3 10-4 h-1.
Dans la suite de cet exercice, on prendra k = 7 × 10−4
.
3. Déterminer le temps de demi-réaction t½
, défini par la relation : t½ =
ln(2) / k.
t½ = ln(2) / (7 10-4) =9,9 102 heures.
.
4. Commenter le résultat précédent en qualifiant de rapide ou lente la
transformation chimique réalisée au laboratoire.
Le temps de demi-réaction est grand : la réaction est lente.
À partir du modèle identifié à la question 1, on montre que la cinétique de l’hydrolyse
du saccharose peut être modélisée par l’équation différentielle (E) :
dc
/d𝑡
= − kc (soit en mathématiques y’ = − ky)
où k = 7 × 10−4
.
5. Résoudre sur [0 ; + +oo[ cette équation différentielle.
c = A exp(-kt) avec A une constante.
6. Sachant que pour t = 0, la concentration initiale du saccharose vaut
0,4 mol ∙ L
−1
, montrer que l’unique solution de l’équation (E) est la fonction c
définie sur [0 ; + +oo[ par c(t) = 0,4 × exp(
−7×10−4×t)
.
c(t=0) = 0,4 = A ; c(t) = 0,4 × exp(
−7×10−4×t).
7. Déterminer la limite de c(t) lorsque 𝑡 tend vers +oo.
Le terme en exponentielle tend vers zéro et c(t) tend vers zéro.
8. Interpréter ce résultat dans le contexte de la production réalisée en laboratoire.
Le réactif saccharose est entiérement consommé.
Exercice 2 ( 6 points).
Naviguer plus vite
Energy Observer est équipé d’un nouveau type de voiles appelées Oceanwings®.
Un système automatisé permet de modifier l’orientation des voiles ainsi que leur
surface exposée au vent (surface totale, voile arisée ou voile affalée).
Le schéma ci-contre représente la voile vue de dessus
ainsi que la force constante exercée par le vent sur la
voile,
notée F vent/voile. La voile, solidaire du bateau, se
déplace de A vers B.
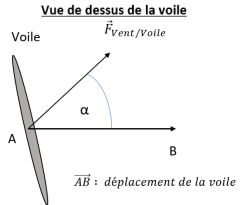
1. Identifier les deux paramètres permettant de faire varier la vitesse du bateau.
Surface de la voile ; orientation de la voile.
2. Déterminer l’expression littérale du travail de la force exercée par le vent sur la
voile au cours du déplacement entre les points A et B.
W = F vent / voile AB cos a.
Pour que le bateau navigue à grande vitesse, le travail de la force exercée par le
vent sur la voile doit être maximum.
3. Déterminer la valeur du paramètre intervenant dans l’expression littérale du
travail afin que celui-ci soit maximum.
cos a = 1 soit a = 0.
4. Expliquer comment varie la vitesse du bateau en augmentant la surface des
voiles et nommer l’énergie du bateau ainsi augmentée.
En augmentant la surface des voiles, la vitesse et l'énergie cinétique du bateau augmentent.
Produire, stocker et restituer l’énergie.
Energy Observer est un bateau autonome en énergie. En l’absence de vent et par
temps couvert, les apports extérieurs d’énergie sont insuffisants. Aussi, les moteurs
électriques qui propulsent le bateau et les appareils à bord font appel à l’énergie
stockée dans des batteries ou sous forme de dihydrogène.
Cette partie se limitera à l’étude de la décharge d’une batterie lithium-ion, qui se
comporte alors comme une pile.
L’électrolyte est un sel de lithium dissous dans un solvant organique.
Les ions lithium Li+ de l’électrolyte peuvent se déplacer d’une électrode à l’autre en
passant au travers d’un séparateur perméable à ces ions.
Au cours de sa décharge, une batterie lithium-ion est le siège de transformations
chimiques qui se déroulent au niveau de chaque électrode selon les équations de
réactions électrochimiques suivantes :
À l’électrode en oxyde métallique : Li(1−x)CoO2(s) + x Li+ + x e
− → LiCoO2(s).
À l’électrode en carbone-graphite : LixC6
(s) → xLi+ x e
− + 6 C(s).
Cet exercice sera traité sans prêter attention à la valeur de x.
5. Justifier que lors de la décharge l’électrode de carbone graphite C(s) est le siège
d’une oxydation.
LixC6
(s) libère des électrons : c'est un réducteur qui s'oxyde.
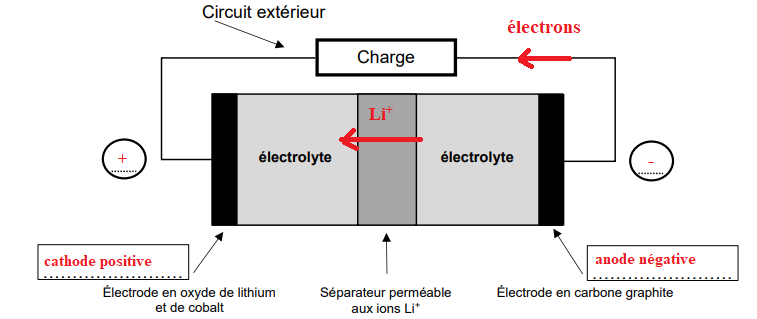
Lors de sa décharge, la batterie délivre un courant électrique dans un circuit
extérieur, comme l’illustre le schéma suivant.
6. Reproduire le schéma de la batterie ci-dessus sur votre copie et y indiquer :
- dans les 2 rectangles les rôles d’anode ou de cathode joués par chaque
électrode ;
- la nature et le sens de déplacement des porteurs de charge circulant dans :
• le circuit extérieur ;
• le séparateur ;
- dans les 2 cercles la polarité de chaque électrode.
Au sujet de l’électrolyte de cette batterie, le solvant organique peut être du carbonate
d’éthylène ou du carbonate de propylène dont les représentations sont données ciaprès :
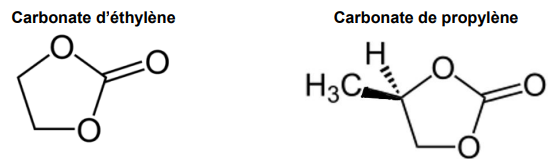
7. Déterminer la formule brute du carbonate d’éthylène.
C3H4O3.
8. Recopier la représentation de la molécule de carbonate de propylène et identifier
la présence de l’atome de carbone asymétrique par une étoile *.
9. Déterminer la configuration absolue R ou S de cet atome de carbone
asymétrique.
10. Représenter l’autre énantiomère de la molécule de carbonate de propylène en
perspective de Cram.
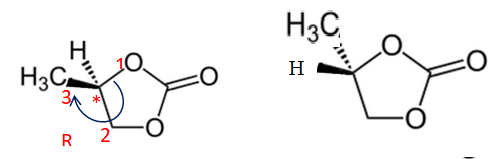
|
...
|
....
|
Exercice 3 ( 4 points)
Question 1
Résoudre dans R l’inéquation :
e 2t > 0,12
.
2t > ln(0,12) ; t > 0,5 ln(0,12).
Question 2
On considère la fonction F définie sur R par F(t) = a e
2t+6
.
a. F est une primitive de la fonction f définie sur R par f(t) = 6 e
2t+6
.
Déterminer la valeur de a.
On dérive F : F '(t) = 2 a e
2t+6
= f(t) = 6 e
2t+6
. Donc a = 3.
b. Donner une autre primitive de la fonction f.
F(t) = a e
2t+6 + constante réelle.
Question 3
On s’intéresse à l’équipement des habitants d’une grande ville en ordinateurs depuis
2000.
La part (exprimée en %) des habitants de cette ville ayant au moins un ordinateur est
modélisée par la fonction f définie sur [0 ; + ∞[ par : f(t) =
94,6
/ (1 + e
0,6−0,2t
) où t est la durée écoulée (en année) depuis l’année 2000.
Montrer que le taux d’équipement ne peut jamais être supérieur à 94,6 %.
On calcule la dérivée f '(t) en posant u = 1; v = 1 + e
0,6−0,2t ; u' = 0 ; v' = -0,2 e
0,6−0,2t ;
(u'v-v'u) / v2 =0,2 e
0,6−0,2t / (1 + e
0,6−0,2t )2 > 0.
La dérivée étant positive, f(t) est strictement croissante de 94,6 / (1+e0,6) ~33,5 à 94,6.
Quand t tend vers l'infini, e
0,6−0,2t tend vers zéro.
Question 4
Soit f la fonction définie sur ]0 ; +∞[ par : f(x) =
ex
/(x
2 + 26x).
Déterminer la limite de la fonction f lorsque x tend vers +oo.
f(x) = ex /[x2(1+26 / x)].
26 / x tend vers zéro ; par croissance comparée ex / x2 tend vers plus l'infini.
Produire de l’énergie avec les panneaux photovoltaïques.
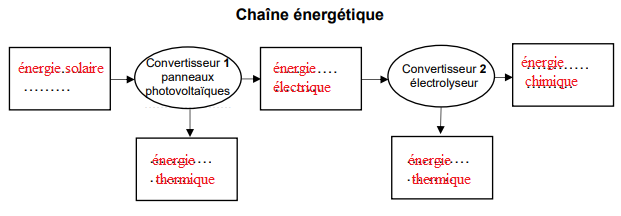
1. Recopier la chaîne énergétique ci-dessous et la compléter en précisant les
formes d’énergie mises en jeu pour fabriquer le dihydrogène à bord du bateau à
partir de l’énergie rayonnée par le Soleil.
La surface globale des panneaux photovoltaïques du bateau est de 168 m2
.
Les panneaux utilisés sont de nouvelle génération et offrent un rendement de 22 %.
On considère que les panneaux solaires du bateau sont soumis à une irradiation
moyenne de 800 W ∙ m−2
.
2. Exploiter la valeur du rendement pour estimer la puissance électrique maximale
fournie par l’ensemble des panneaux du bateau.
800 x 168 x0,22 =2,96 104 ~3,0 104 W ou 30 kW
Le constructeur des panneaux annonce que l’installation photovoltaïque sur ce
bateau est capable de produire une puissance électrique maximale de 28 kW.
3. Comparer le résultat précédent avec la valeur de la puissance électrique
maximale annoncée par le constructeur, puis commenter.
Ecart relatif (30 -28) / 28 x100 =7 %.
Les valeurs sont en accord à 7 % près.
Les panneaux photovoltaïques sont constitués de cellules identiques montées en
série.
Considérons une cellule photovoltaïque soumise à une irradiation solaire de
800 W ∙ m−2 et à une température de 20 °C.
Dans ces conditions, les caractéristiques électriques d’une cellule photovoltaïque
sont données par le graphique suivant :
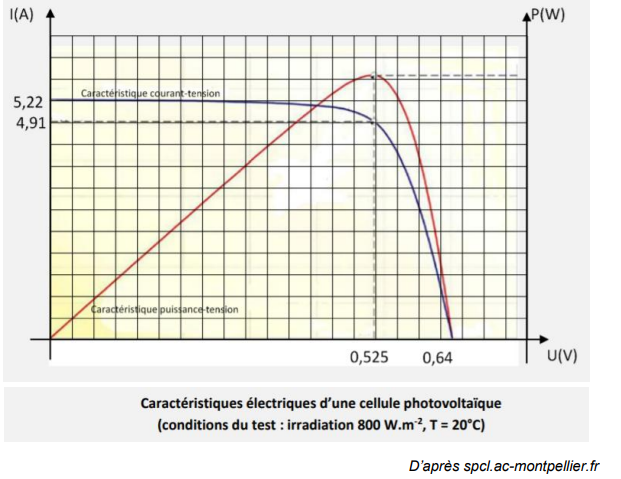
4. Montrer que, dans ces conditions, la valeur de la puissance électrique maximale
délivrée par une cellule est voisine de 2,6 W.
La puissance est maximale si I = 4,91 A et U = 0,525 V.
Pmax = U I = 0,525 x4,91 ~2,6 W.
5. Déterminer le nombre de cellules nécessaires pour atteindre la valeur de la
puissance maximale annoncée par le constructeur.
28 104 / 2,6 ~1,1 105.
6. Montrer que l’énergie électrique maximale produite par l’installation
photovoltaïque au cours d’une semaine est de l’ordre de 1600 kWh si les
conditions sont satisfaites pendant huit heures par jour (unités d’énergie : 1 Wh =
3600 J).
28 x8 x7~1,6 103 kWh.
L’énergie ainsi produite sert à l’alimentation électrique des électrolyseurs qui
réclament une énergie d’environ 2400 kWh pour faire le plein des réservoirs de
dihydrogène.
7. Estimer la durée nécessaire pour remplir pleinement les réservoirs en
dihydrogène seulement par l’apport d’énergie des panneaux photovoltaïques.
Commenter cette durée.
2400 / 28~86 heures ( environ 11 jours à 8 heures d'ensoleillement).
Les panneaux solaires sont insuffisant pour assurer l'autonomie..
Le dihydrogène pour la pile à combustible.
Le stockage du dihydrogène est réalisé dans huit réservoirs de 332 L, soit
l’équivalent en énergie de 230 L d’essence. Ce volume représente une énergie
globale nette stockée de 1000 kWh.
Cette pile à combustible est constituée de 400 cellules élémentaires.
Au cours de son fonctionnement, chaque cellule élémentaire consomme du
dihydrogène H2
(g) issu des huit réservoirs de stockage et du dioxygène O2
(g)
provenant de l’air ambiant. L’équation de la réaction modélisant le fonctionnement de
la pile est la suivante :
O2
(g) + 2H2
(g) → 2H2O(l).
8. Écrire les équations des réactions électrochimiques modélisant les
transformations chimiques se produisant à l’anode et à la cathode.
Oxydation à l'anode négative : 2H2(g) --> 4H+aq + 4e-.
Réduction à la cathode positive : O2(g) + 4H+aq + 4e- --> 2 H2O(l).
Le courant électrique circulant dans chaque cellule élémentaire a pour intensité : I = 170 A.
Les réservoirs permettent de stocker un total de 62 kg de dihydrogène.
9. À l’aide des informations recueillies, montrer que la quantité de matière de H2(g)
disponible pour chaque cellule élémentaire vaut 78 mol.
62 103 / M(H2) =62 103 / 2 = 3,1 104 mol pour 400 cellules.
3,1 104 / 400 ~ 78 mol..
10. En déduire la quantité de matière n(e
−) d’électrons échangés par une cellule.
n(e
−) = 2 n(H2) = 78 x2 =156 mol.
La durée d’autonomie de la pile correspond à la durée de fonctionnement Dt d’une
cellule qui s’exprime en secondes par la relation :
Dt = n(e
−) × F / I.
11. Déterminer la durée d’autonomie de la pile à combustible en secondes, puis en
heures. Conclure sur l’intérêt de constituer une réserve de dihydrogène à bord.
Dt =156 x 96500 / 170=8,85 104 s ou 24 h 36 min par cellule élémentaire.
L'hydrogène complète l'énergie apportée par les panneaux photovoltaïques et permet l'autonomie en énergie du bateau.
|
|