Dans ce tube à rayons X, une tension élevée U est maintenue entre un filament cathodique,
borne négative, et une anode tournante, borne positive. Un courant électrique
provoque l'échauffement d'un filament situé à la cathode. L’agitation des électrons présents
augmente et une partie d’entre eux est éjectée du filament au point O, avec une vitesse
négligeable. La tension U accélère les électrons du point O vers l'anode en tungstène.
Devenus très énergétiques, ils frappent l’anode, ce qui produit des rayons X.
Pour obtenir ces rayons X, chaque électron doit avoir acquis une énergie cinétique égale à
6,4 × 10
-15 J au minimum.
Le but de cet exercice est de calculer la tension minimale à appliquer entre la cathode et
l’anode pour que le faisceau d’électrons parvienne à provoquer l’émission de photons X au
niveau de l’anode.
On considèrera l’électron comme système d’étude assimilé à un point matériel dont on
négligera le poids.
Son mouvement sera étudié dans un référentiel terrestre considéré comme galiléen.
À l’instant initial, l’électron est situé au point O et sa vitesse est considérée comme nulle.
Données : Masse de l’électron : m = 9,1 × 10
-31 kg.
Charge de l’électron : q = - e = - 1,6 × 10
-19 .
C
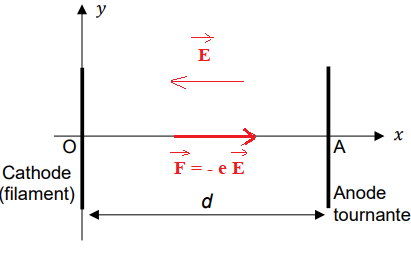
1. Reproduire la figure puis tracer, entre la cathode et l’anode, sans préciser d’échelle :
- le vecteur champ électrique supposé uniforme E,
- la force F que subit un électron situé en un point de l’axe (Ox).
2. Donner l’expression vectorielle de F en fonction de e et E.
 3.
3. Montrer que les coordonnées du vecteur accélération de l’électron, exprimées dans le
repèresont a
x = e × U
/ (m × d) et a
𝑦 = 0.
Le poids étant négligeable, l'électron n'est soumis qu'à la force électrique F. La seconde loi de Newton conduit à :
a
x = e E / m avec E = U / d ; a
y = 0.
4. En déduire la coordonnée du vecteur vitesse de l’électron selon l’axe (Ox), notée v
x .
Établir que x s’écrit ½eU * (md) t
2.
La vitesse est une primitive de l'accélération : v
x(t) = eU / (md) t + Cste.
vx(t=0) =Cste = 0.
vx(t) = eU / (md) t.
La position est une primitive de la vitesse : x(t) = ½eU /(md) t2 + Cste.
x(t=0) = Cste = 0.
5. Donner l’expression littérale de t
A , l’instant où l’électron atteint l’anode (au point A) située
à la distance d de O.
d =
½eU /(md) tA2.
tA2 = 2md2 / (eU) ; tA = d [2 m /(eU) ]½.
6. Grâce aux deux questions précédentes, en déduire que l’expression de la vitesse de
l’électron au niveau de l’anode est
v
A = (2eU / m)
½.
vA = eU / (md) tA=eU / (md) d [2 m /(eU) ]½ = (2eU / m)½.
vA =[2 x1,6 10-19 U / (9,1 10-31)]½ =5,96 105 U½.
7. Répondre à la problématique de l’exercice « trouver la tension minimale à appliquer entre
la cathode et l’anode pour que le faisceau d’électron parvienne à provoquer l’émission
de photons X an niveau de l’anode ».
Energie cinétique minimale de l'électron en A:
½mv
A2 =6,4 10
-15 ;
vA2 =1,40 1016 =3,55 1011 U.
U = 3,9 104 V = 39 kV.