Extraction du gaz de schiste par électro-fracturation, bac général Réunion 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... L’électro-fracturation est une méthode actuellement à l’étude pour remplacer la fracturation hydraulique et extraire le gaz de schiste. L’objectif de cet exercice est d’étudier la charge et la décharge des condensateurs en se basant sur les données d’une expérimentation menée à l’université de Pau et des Pays de l’Adour. 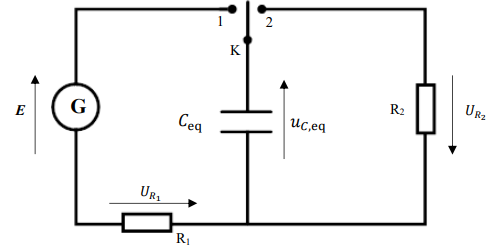L’installation électrique permettant d’alimenter les électrodes peut être modélisée de façon simplifiée par un schéma électrique contenant  : - un interrupteur deux positions K ; - une alimentation électrique de tension E = 40 kV ; - une installation permettant d’intégrer de 1 à 6 condensateurs placés en parallèle, chacun de capacité C = 200 nF, représentée par un condensateur équivalent de capacité Ceq ; - un conducteur ohmique de résistance R1 = 160 kW ; - le système {électrodes + eau} qui peut être modélisé par un conducteur ohmique de résistance R2 = 100 W.   PARTIE A : Charge du condensateur équivalent.  Dans cette partie, nous allons étudier la charge du condensateur équivalent de capacité Ceq pour déterminer l’énergie maximale stockée Wmax. Le condensateur équivalent est initialement déchargé et l’on ferme l’interrupteur K en position 1 à l’instant t = 0 s. A.1. Établir l’expression liant la tension aux bornes du condensateur équivalent uC,eq, celle aux bornes du conducteur ohmique uR1 , et la tension aux bornes de l’alimentation E. Additivité des tensions : E =uR1 +uC,eq. A.2. Établir l’équation différentielle qui régit l’évolution de la tension uC,eq, aux bornes du condensateur équivalent lors de la charge. uR1 = R1 i avec i = dq/dt = R1Ceq duC,eq /dt. E = uC,eq +R1Ceq duC,eq /dt. (1) A.3. Vérifier que la solution de cette équation différentielle s’écrit : uC,eq. = E × (1 − exp( - t / tcharge)). duC,eq /dt = E /  tcharge exp( - t / tcharge). Repport dans (1) : E = E × (1 − exp( - t / tcharge)) +R1Ceq E /  tcharge exp( - t / tcharge). Cette égalité est vérifiée si tcharge =R1Ceq .  A.4. Déterminer la capacité Ceq du condensateur équivalent. On détaillera le raisonnement et fera apparaître clairement une partie de la démarche sur la courbe suivante. 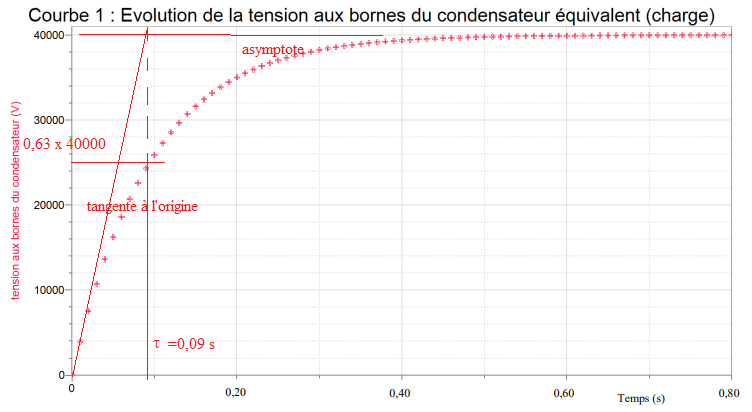0,09 = R1Ceq  =1,6 105 Ceq. Ceq =0,09 / (1,6 105) =5,6 10-7 F. A.5. En déduire le nombre de condensateurs de capacité C = 200 nF utilisés lors de l’expérimentation. 5,6 10-7 / (200 10-9)~ 3. A.6. Déterminer l’énergie maximale Wmax stockée dans le condensateur équivalent chargé. Wmax= ½Céq E2 =0,5 x 5,6 10-7 x(40 103)2=4,5 102 J. ... .... PARTIE B : Décharge du condensateur équivalent.  Avant l’apparition d’un arc électrique entre les deux électrodes, le condensateur équivalent est initialement chargé avec une tension E = 40 kV, puis il subit une pré-décharge pendant une durée Dt = 12 µ𝑠. On considérera pour la suite de l’exercice que Ceq = 600 nF. Durant cette pré-décharge, la tension aux bornes du condensateur équivalent évolue selon l’expression u C,eq(t) = E × exp(- t / (R2Ceq)) . À t= 0 s, on ferme l’interrupteur K en position 2. B.1. Déterminer la valeur de la tension u C,eq(t = Dt) aux bornes du condensateur équivalent à la fin de la pré-décharge. R2Ceq =100 x 600 10-9=6,0 10-5 =60 µs. u C,eq(t=12 10-6) = 40 × exp(- 12 / 60)=32,749 ~32,7 kV.  B.2. En déduire la valeur de l’énergie restante Warc dans le condensateur équivalent et disponible pour la création de l’arc électrique. Warc= ½Céq E2 =0,5 x 6 10-7 x(32,7 103)2=3,2 102 J.  B.3. Calculer le rendement énergétique h de l’installation étudiée permettant la création de l’arc électrique. Commenter. h = Warc / Wmax =3,2 / 4,5 ~0,71 (71 %); valeur assez élevée.

menu