Le TWEENER-LOB ou le coup entre les jambes, bac général Réunion 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Lors des huitièmes de finale de Roland Garros en 2022, Carlos Alcaraz a réalisé un « tweener-lob » contre Karen Khachanov. Pour que le « tweener-lob » soit réussi, la balle doit passer au-dessus de l’adversaire et retomber avant la ligne de fond de court. On s’intéresse dans cet exercice à ce geste tennistique. L’étude sera menée dans le référentiel terrestre supposé galiléen et le système {balle} sera considéré comme un point matériel noté G. On négligera tout type de frottement. Carlos Alcaraz est situé sur la ligne de fond de court lorsqu’il joue son « tweener-lob ». Il frappe la balle à une hauteur y0 = 30,0 cm et lui communique une vitesse v0 contenue dans un plan vertical, de valeur 𝑣0 = 55,1 km ⋅ h −1 , et formant un angle a = 48,0° avec l’horizontale. 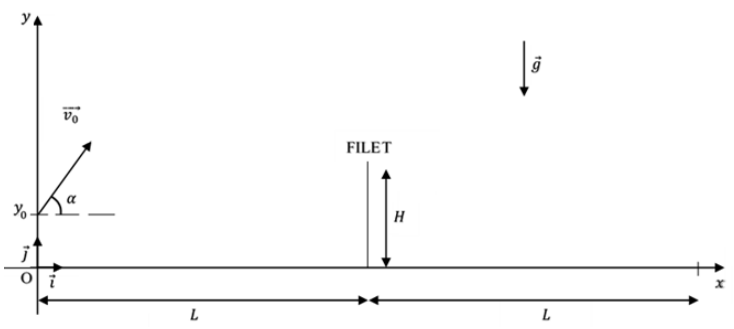- masse de la balle : m = 58,5 g ; - longueur entre la ligne de fond de court et le filet : L = 12,0 m ;  - hauteur du filet : H = 0,914 m. PARTIE A : Étude du mouvement de la balle lors du « tweener-lob » A.1. En appliquant la deuxième loi de Newton, déterminer les coordonnées du vecteur accélération lors du mouvement de la balle dans le repère (O; i ;j ). La balle n'est soumise qu'à son poids ; la chute est libre. La seconde loi de Newton conduite à : ax=0 ; ay = -g. La balle est frappée à la date t = 0 s.  A.2. Déterminer, en détaillant chaque étape de votre raisonnement, les équations horaires x(t) et y(t) du point 𝐺 dans le repère (O;i ;j ). La vitesse est une primitive de l'accélération : vx = A , vy = -gt + B avec A et B des constantes. A t=0 : vx = v0 cos a = A ; vy = B =v0 sin a . vx = v0 cos a  ; vy = -gt +v0 sin a . La position est une primitive de la vitesse : x =v0 cos a  t + C ; y = -½gt2 +v0 sin a t + D avec C et D des constantes. A t=0 : x = C =0 ; y =D = y0.  x =v0 cos a  t  ; y = -½gt2 +v0 sin a t + y0. A.3. En déduire que l’équation de la trajectoire de la balle est, dans les unités du système international :  y = −0,047 x2 + 1,1x + 0,30. t = x / (v0 cos a); repport dans y : y = -½g x2 (v0 cos a)2+ x tan a  + y0. v0 = 55,1 / 3,6 =15,3 m/s. y = -4,9 /(15,3 x0,669)2+1,11 x +0,30.  y = −0,047 x2 + 1,1x + 0,30.  A.4. L’adversaire Karen Khachanov se situe à 3,0 m du filet et le tamis de sa raquette est alors à une hauteur de 4,0 m lorsque Carlos Alcaraz tente de le lober. Déterminer si la balle jouée par C. Alcaraz passe au-dessus de la raquette de son adversaire. x =15 m. y = -0,047 x152 +1,1 x15 +0,30=6,2 m La balle jouée par C. Alcaraz passe au-dessus de la raquette de son adversaire. ... .... PARTIE B : Étude énergétique du mouvement de la balle.  On choisira un axe vertical ascendant et une énergie potentielle de pesanteur nulle à l’origine du repère. À t = 0 s, la balle est située au point (x0 = 0 ; 𝑦0 = 0,30 m) avec une vitesse v0 = 55,1 km ⋅ h −1 . B.1. Rappeler la définition de l’énergie mécanique Em de la balle. L'énergie mécanique est la somme des énergies potentielles et cinétique.  B.2. Exprimer l’énergie mécanique Em(0) de la balle à t = 0 s, en fonction de m, g, v0 et y0. Calculer sa valeur. Em(0) =½mv02 + mgy0. Em(0) = 0,5 x0,0585 x15,32 +0,0585 x9,81 x 0,30 =6,85 +0,17=7,02 ~7,0 J  B.3. Indiquer sous quelle condition s’applique la conservation de l’énergie mécanique. En absence de frottement ( ou de forces dites "non conservatives"), l'énergie mécanique se conserve. B.4. Calculer la valeur de la vitesse de la balle vf quand elle retombe au sol. Indiquer si la valeur réellement mesurée par le radar du terrain sera supérieure ou inférieure à celle calculée. Justifier. Conservation de l'énergie mécanique : 7,02 = ½mvf2. vf=(14,04 /0,0585)½ = 15,5 m /s. La vitesse réelle sera inférieure, la balle est soumise au frottement de l'air.

menu