Sujet 1.
On considère le cube ABCDEFGH ci-dessous tel que AB = 1.
On note M le centre de la face BCGF et N le centre de la face EFGH.
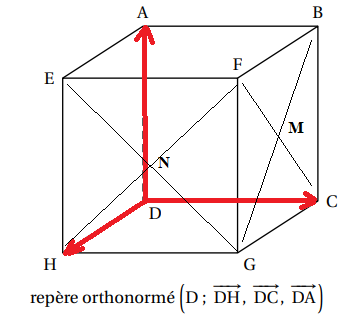 1.
1. Donner sans justifier les coordonnées des points F et C.
F( 1 ; 1 ; 1) ; C(0 ; 1 ; 0).
2. Calculer les coordonnées des points M et N.
x
M =(x
C+x
G) / 2= (0 +1) / 2 = 0,5.
yM =(yC+yB) / 2= (1 +1) / 2 = 1.
zM =(zC+zB) / 2= (0 +1) / 2 = 0,5.
M(0,5 ; 1 ; 0,5).
xN =(xH+xG) / 2= (1 +1) / 2 = 1.
yN =(yH+yG) / 2= (0 +1) / 2 = 0,5.
zN =(zH+zE) / 2= (0 +1) / 2 = 0,5.
N(1 ; 0,5 ; 0,5).
3. a. Démontrer que le vecteur AG est normal au plan (HFC).
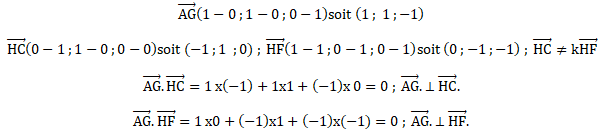 b.
b. En déduire une équation cartésienne du plan (HFC).
x +y -z +d = 0.
H appartient à ce plan :
xH +yH -zH +d = 0.
1 +0 -0 +d = 0 ; d = -1.
x +y -z-1=0.
4. Déterminer une représentation paramétrique de la droite (AG).
Coordonnées d'un vecteur directeur de cette droite : (1 ; 1 ; -1).
x = t +x
A = t ;
y = t +yA = t ; z = -t +zA = -t+1 avec t réel.
5. Démontrer que le point R de coordonnées (
2
/3
;
2/
3
;
1/
3 )
est le projeté orthogonal du point G sur le
plan (HFC).
R appartient à la droite (AG) orthogonale au plan ( HFC) : x
R = t =2 /3 ; y
R = t = 2 /3 ; z
R = -2/3+1 = 1 /3.
Hypothèse : R appartient au plan (HFC) :
x
R +y
R -z
R -1 =2 /3 +2 / 3-1 /3 -1 =0 est vérifié.
L'hypothèse est valide.
6. On admet qu’une représentation paramétrique de la droite (FG) est :
x = 1;
y = 1;
z = k
(k réel).
Démontrer qu’il existe un unique point K sur la droite (FG) tel que le triangle KMN soit rectangle
en K.
KM
2 =(0,5 -1)
2 +(1-1)
2 +(0,5-k)
2=0,25 +0,25 +k
2 -k=
k2 -k+0,5.
KN2 =(1 -1)2 +(0,5-1)2 +(0,5-k)2=0,25 +k2 -k+0,25= k2 -k+0,5.
MN2 =(0,5 -1)2 +(0,5-1)2 +(0,5-0,5)2=0,5.
Hypothèse : le triangle KMN soit rectangle
en K.
k2 -k+0,5 + k2 -k+0,5 =0,5.
2k2-2k+0,5 = 0 ; k2-k+0,25 =0 ; (k-0,5)2 =0 ; solution unique k = 0,5.
K( 1 ; 1 ; 0,5).
7. Quelle fraction du volume du cube ABCDEFGH le volume du tétraèdre FNKM représente-t-il ?
La base est le triangle KNM :
aire de ce triangle : KM x KN / 2 ; KM =KN = (
k2 -k+0,5)
½ =
( 0,52 -0,5+0,5)½ =0,5.
Aire = 0,5 x0,5 / 2 = 0,125.
Hauteur du tétraèdre relative à la base KNM : FK.
FK= [(1-1)
2 +(1-1)
2 +(1-0,5)
2]
½ =0,5.
Volume de ce tétraèdre : aire de base x hauteur / 3 = 0,125 x0,5 /3 = 1/8 x1 /2 x1 /3 = 1 /48.
Volume du cube : 1 unité de volume.
Le volume du tétraèdre FNKM représente 1/48 éme du volume du cube.