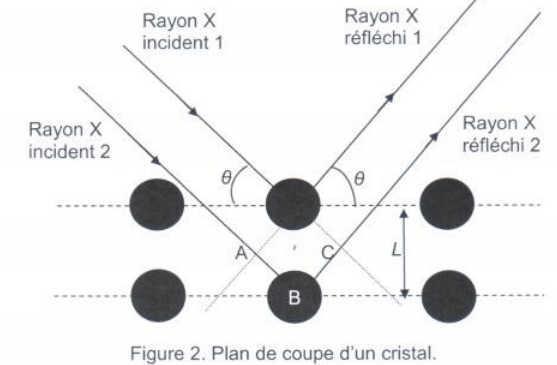
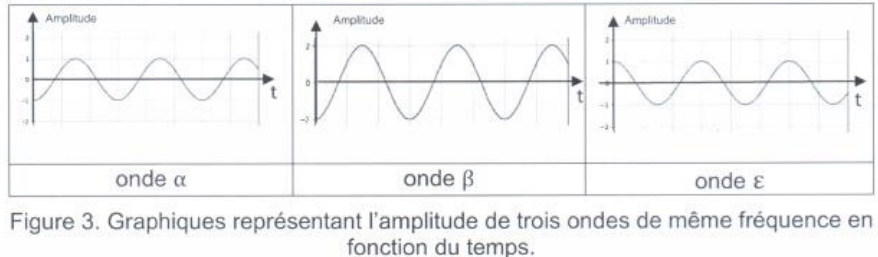
Production de rayons X.
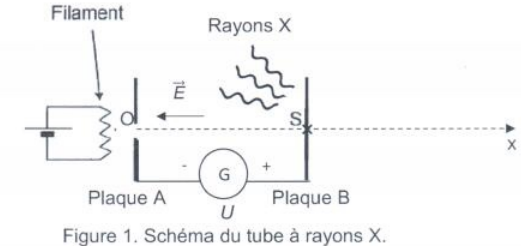
Les plaques A et B sont assimilées aux armatures d'un condensateur plan alimenté par un générateur de tension G.
Le filament chauffé par effet Joule produit des électrons qui sont accélés entre les armatures.
Les électrons percutent les atomes de la plaque B et provoquent l'émission des rayons X.
On s'intéresse à un électron issu du point O sans vitesse initiale et accéléré jusqu'au point S de la plaque B.
U = 20,0 kV ; OS = d = 1,00 cm ; masse de l'électron m = 9,1 10-31 kg ; e = 1,60 10-19 C.
1. Exprimer la force électrique F subie par l'électron et la représenter.
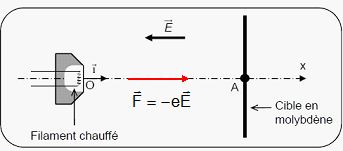
2. On néglige le poids de l'électron, établir l'expression de l'accélération de l'électron.
Selon l'axe Ox, la seconde loi de Newton s'écrit : ma = F = e E ; a = e/m E.
3. Montrer que la vitesse s'écrit v(t) = e / m Et et établir l'équation horaire x(t).
La vitesse est une primitive de l'accélération : v(t) = at +Cste.
La vitesse initiale étant nulle : v(t) = at = e / m E t.
x(t) = ½at2 + Cste =½at2 ( x(t=0) = 0).
4. Montrer que la vitesse de l'électron en S vaut 8,38 107 m/s.
E = U / d =20,0 103 / 0,01 = 2,0 106 V / m ; d = ½e / m E t2 ; t2 = 2 d m /(eE)=2 x0,01 x9,1 10-31 / (1,6 10-19 x2 106)=5,7 10-20.
t =2,4 10-10 s ; v =1,6 10-19 x2 106 x2,4 10-10 / (9,1 10-31)=8,38 107 m/s.
Autre méthode : théorème de l'énergie cinétique entre O et S :
½m v2 -0 = travail de la force électrique = e U.
v = (2eU/m)½ =(2 x1,6 10-19 x2,0 104 /(9,1 10-31))½ =8,38 107 m/s.
En S pour provoquer l'émission de rayons X, l'énergie cinétique de l'électron doit être supérieure à 6,90 104 eV.
5. L'énergie cinétique de l'électron est-elle suffisante ?
Energie cinétique de l'électron en S = e U = 1,6 10-19 x2 104 =3,2 10-15 J.
3,2 10-15 / (1,6 10-19) =.2,0 104 eV, valeur insuffisante.
6. Parmi les deux
tensions électriques suivantes 5 kV et 70 kV quelle est celle qui
permettrait d'augmenter l'énergie cinétique de l'électron ?
Energie cinétique de l'électron en S = e U : U doit être supérieure à 20 kV, donc on retient 70 kV.