L'expérience
de Millikan,
bac général Polynésie
09 /2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
L’objectif
de cet exercice est de comprendre comment des physiciens de
l’université de Gothenburg en Suède ont directement observé en 2021 la
proportionnalité entre la charge totale Q portée par une goutte d’huile
et la charge élémentaire e.
Établissement d’un champ électrique uniforme entre les plaques du condensateur plan.
Les chercheurs ont utilisé pour former un condensateur plan C, deux plaques métalliques, séparées par un diélectrique.
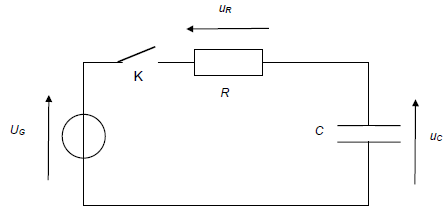
On réalise un circuit électrique comprenant un générateur délivrant une tension continue U G égale à 666 V, un conducteur ohmique de résistance R de valeur égale à 10 M W
et le condensateur de capacité C. Un interrupteur K permet de fermer ou
d’ouvrir le circuit. À la date t = 0 s, le condensateur est
initialement déchargé.
 Q1
Q1. Écrire la relation existante entre les tensions u C, u R et U G du circuit.
uC+ uR = UG .
Q2. Á l’aide de la relation précédente, montrer que l’équation différentielle régissantl’évolution de la tension uC(t) aux bornes du condensateur lors de la charge est : duc(t)dt + 1/(RC)uc(t) = UG/ (RC).
q = CUC ; i = dq /dt = CdUC/dt.
uc +Ri = uG ; uc +RCdUc/dt = uG ;
duc(t)/dt + 1/(RC)uc(t) = UG/ (RC).
Q3. Vérifier que la solution de cette équation différentielle est uc(t) = UG × (1- e(-t / t)) en précisant l’expression de la constante t.
duc(t)/dt =uG/ t e(-t / t) ; repport dans l'équation différentielle :
uG/ t e(-t / t)+uG / (RC) (1- e(-t / t))= uG/ (RC).
uG/ t e(-t / t)=uG / (RC)e(-t / t) est bien vérifiée si t = RC.
La figure suivante représente l’évolution de la tension uc(t) aux bornes du condensateur lors de sa charge.
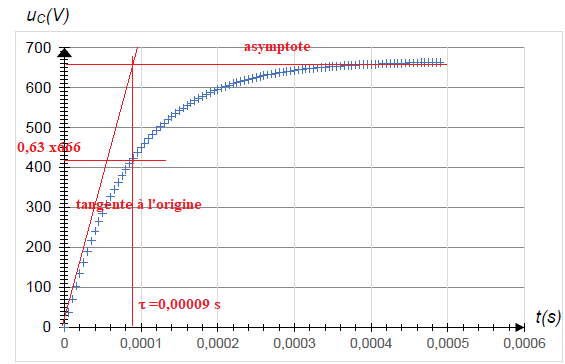
Q4. Déterminer, à l’aide de la figure , la valeur du temps caractéristique de charge t en expliquant la démarche.
Q5. En déduire la valeur de la capacité C du condensateur utilisé.
RC = 9 10-5 ; C = 9 10-5 / 107=9 10-12 F.
Données :
La capacité (en F) d’un condensateur plan : C = e × S /d où, S est la surface d’une plaque de valeur égale à 10,0×10−4 m2, e la permittivité diélectrique du milieu en F·m–1 et d la distance entre les plaques de valeur égale à 1,0×10−3 m.
La valeur de la permittivité diélectrique e du milieu est égale à 8,85×10–12 F·m–1.
Q6. Retrouver la valeur de la capacité C du condensateur utilisé en la calculant à partir des données précédentes.
C = 8,85×10–12 x10,0×10−4 /(1,0×10−3)=8,85×10–12 F.
L’expérience des chercheurs de l’université de Gothenburg.
À l’université de Gothenburg, les scientifiques ont imaginé
l’expérience suivante : une goutte d’huile de silicone, initialement
neutre, est alors piégée grâce à un « piège optique » généré par une
source laser de longueur d’onde l de
valeur égale à 532 nm entre les plaques du condensateur utilisé
précédemment. Une source radioactive émettrice de particules permet
alors de charger les différentes gouttes d’huile de silicone au cours
du temps comme représenté sur la figure.
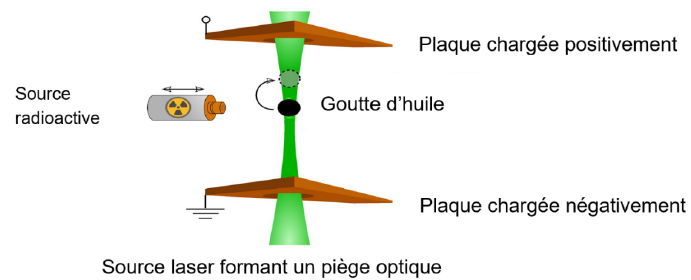
Q7. Préciser le domaine de longueurs d’onde à laquelle appartient la source laser utilisée dans l’expérience suédoise.
532 nm est compri entre 400 nm et 800 nm : domaine du visible.
La source radioactive est de l’américium qui subit une désintégration
ionisant les molécules présentes entre les plaques du condensateur et
libérant des électrons.
Q8. Préciser le sens de déplacement de la goutte si la source radioactive permet de la charger négativement.
La goutte d'huile chargée négativement se déplace vers l'armature positive du condensateur.
Grâce au piège optique initié par la source laser, les chercheurs
observent alors que la goutte initialement neutre se déplace par sauts
successifs au cours du temps. Une représentation du déplacement de la
goutte se trouve à la figure.
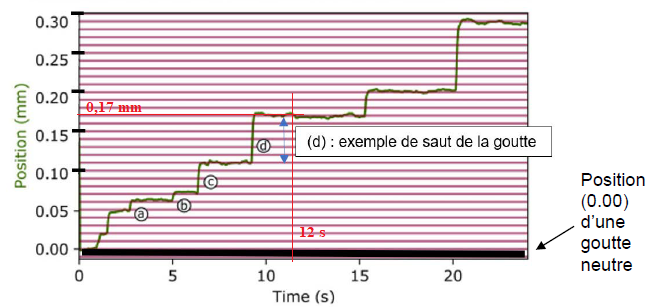
À chaque fois que la goutte d’huile gagne un électron, elle se déplace d’une hauteur h fixe comme en (a) ou (b) sur la figure.
Q9. Évaluer, à
l’aide de la figure 4, la hauteur h en millimètre d’un saut de la
goutte correspondant au gain d’un seul électron comme en (a) ou en (b).
0,06-0,05 = 0,01 mm
Q10. Déterminer le nombre de charges électriques élémentaires acquises par la goutte au bout d’un temps t de valeur égale à 12 s.
0,17 /0,01=17 charges élémentaires.
Q11. En déduire, à
l’aide de la figure 4, que cette expérience permet bien d’observer la
proportionnalité entre la charge totale Q de la goutte d’huile et la
charge élémentaire e.
Q = 17 e au bout de 12 s.
|
...
|
....
|
Bilan de forces entre les plaques du condensateur utilisé dans l’expérience historique de Millikan.
Dans l’expérience
historique de Millikan, une goutte d’huile de volume V et de masse m,
initialement chargée négativement tombe par l’intermédiaire d’un petit
trou entre les plaques du condensateur initialement déchargé. Le
diélectrique présent entre les plaques est l’air.
La goutte est donc
soumise à son poids P lors de sa chute. En outre, la goutte est
également soumise à une force de frottement f à cause de l’air présent
entre les plaques du condensateur. La masse volumique de l’air étant
mille fois plus petite que la masse volumique de l’huile, on peut
négliger la poussée d’Archimède qui s’exerce sur la goutte.
Q12. Écrire la
relation vectorielle, en utilisant la deuxième loi de Newton, existante
entre ces forces et l’accélération a de la goutte d’huile considérée
comme ponctuelle de masse m au cours de sa chute en précisant le
référentiel choisi.
Référentiel du laboratoire.
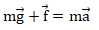 ( condensateur déchargé). ( condensateur déchargé).
Q13. Indiquer une
des différences entre l’expérience historique réalisée par Millikan et
l’expérience proposée par l’équipe suédoise concernant les gouttes
d’huile.
Dans l'expérience historique, la charge de la goutte est constante.
Une simulation a permis
de tracer la courbe de l’évolution de la vitesse v d’une goutte d’huile
de silicone au cours de sa chute lors de l’expérience historique .
On distingue alors deux phases dans le mouvement de la goutte. La
première phase est appelée le régime transitoire alors que la seconde
porte le nom de régime stationnaire.
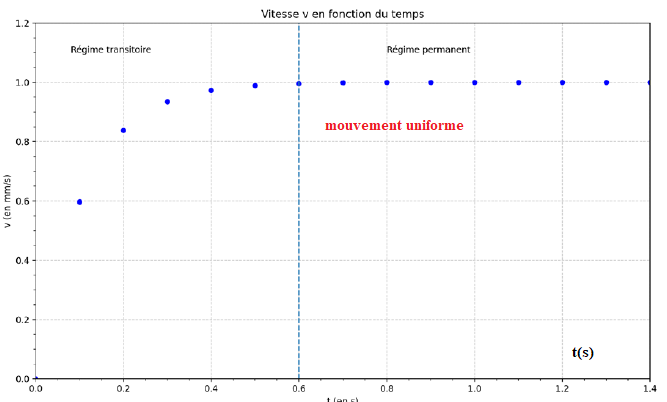
À la date t = 0,6 s, on considère que le vecteur vitesse v de la goutte ne varie plus.
Q14. Décrire la
nature du mouvement de la goutte entre les plaques du condensateur à
partir de cette date t. En déduire la relation vectorielle reliant les
forces s’appliquant sur le système dans le référentiel choisi
précédemment.
Mouvement rectiligne uniforme : la somme vectorielle des forces est nulle.
Le régime stationnaire étant atteint, on génère un fort champ
électrique E qui induit l’apparition d’une force électrique F qui
s’ajoute aux précédentes.
Q15. Reproduire
sans souci d’échelle le vecteur force F correspondant à la force
électrique supplémentaire à laquelle la goutte d’huile, chargée
négativement, est soumise.
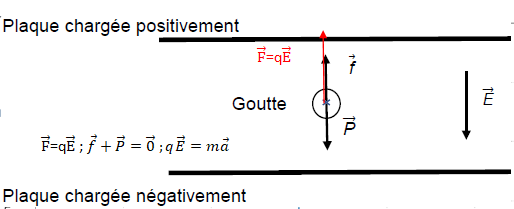
La charge des gouttes étant négative, la force électrique est colinéaire au champ mais de sens contraire.
Q16.
En déduire la nature du mouvement de la goutte quand un champ
électrique suffisamment élevé règne entre les plaques du condensateur
dans le référentiel choisi.
Phase 1 : mouvement rectiligne uniformément décéléré, verticale vers le
bas ( accélération et vitesse initiale de sen contraire) jusqu'à l'arrêt
Phase 2 : mouvement rectiligne uniformément accéléré, verticale vers le haut, puis mouvement rectiligne uniforme quand les forces se compensent.
|
|