Suites, Mathématiques, bac général Polynésie 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Sujet 1. Soit (un ) la suite définie par u0 = −1 et, pour tout entier naturel n : un+1 = 0,9un − 0,3. 1. a. Démontrer par récurrence que, pour tout n entier naturel, un = 2 × 0,9 n − 3. Initialisation : u1 = 0,9u0-0,3 = -0,9-0,3 = -1,2 = 2 x0,9 x1 -3. La propriété est vraie au rang 1. Hérédité : un = 2 × 0,9n − 3 est supposée vraie. un+1 = 0,9un − 0,3. un+1 = 0,9 x(2 x0,9n-3)-0,3 =2 x0,9n+1 -2,7-0,3=2 x0,9n+1  -3. Conclusion : la propriété est vraie au rang 1 et héréditaire ; elle est vraie pour tout entier naturel  n.  b. En déduire que pour tout entier naturel, −3 < un ≤ −1. 0 < 0,9 < 1 implique 0 <0,9n < 1. Multiplier par 2 : 0 < 2 x0,9n < 2. Ajouter -3 : -3 < 2 x0,9n -3< -1.  c. Démontrer que la suite (un) est strictement décroissante. u0 = -1 ; quand n tend vers l'infini 0,9n tend vers zéro et un tend vers -3. un+1-un =2 x0,9n+1  -3 -(2 × 0,9 n − 3)=2 x 0,9n(0,9-1) < 0. La suite est décroissante de 0 à -3  d. Démontrer que la suite (un) converge et préciser sa limite. La suite est décroissante et minoré par -3, donc elle converge vers -3.  2. On se propose d’étudier la fonction g définie sur ]−3 ; −1] par : g(x) = ln(0,5x + 1,5) − 𝑥. a. Justifier toutes les informations données par le tableau de variations de la fonction g (limites, variations, image de −1). 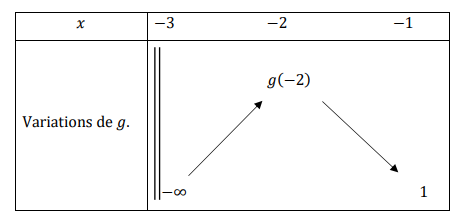Quand x tend vers -3 : g(x) tend vers ln(0) +3 soit vers moins l'infini. Quand x tend vers -1 : g(x) tend vers ln(1)+1 = 1 g '(x) = 0,5 /(0,5x+1,5) -1 = (-0,5 x -1) / (0,5x+1,5). g'(x) =0 pour x = -2. g'(x) < 0 pour x > -2 et g(x) est décroissante. g'(x) > 0 pour x < -2 et g(x) est croissante. g(x) présente un maximum g(-2) =ln(0,5)+2 ~1,31. b. En déduire que l’équation g(x) = 0 a exactement une solution que l’on notera a et dont on donnera un encadrement d’amplitude 10−3 . D'après le théorème des valeurs intermédiaires sur ]-3 ; -2(, g(x) est strictement croissante de moins l'infini à ln(0,5)+2 > 0 et continue sur cet intervalle : il existe donc un réel a unique tel que g(x) = 0. La calculatrice donne  : -2,889  < a < -2,888. 3. Dans la suite de l’exercice, on considère la suite (vn) définie pour tout entier naturel, par : vn = ln(0,5 un + 1,5). a. En utilisant la formule donnée à la question 1. a., démontrer que (vn ) est arithmétique de raison ln(0,9). un = 2 × 0,9 n − 3. vn = ln(0,5 un + 1,5) = ln( 0,9 n )= n ln(0,9). Il s'agit donc d'une suite arithmétique de raison ln(0,9). b. Soit n un entier naturel. Démontrer que un = vn si, et seulement si g(un) = 0. un = vn implique un = ln(0,5 un + 1,5). ln(0,5 un + 1,5)-un=0 implique g(un) = 0. c. Démontrer qu’il n’existe aucun rang k ∈ N pour lequel uk = a. d. En déduire qu’il n’existe aucun rang k ∈ N pour lequel vk = uk. Donc g(un) = 0 implique un = a =2 x0,9n-3. Or -2,889 < a < -2,888 : on en déduit que : -2,889 < 2 x0,9n-3 < -2,888. Ajouter 3 :  0,111 < 2 x0,9n < 0,112.. 0,0555 < 0,9n < 0,0556. La fonction logarithme népérien étant croissante : ln(0,0555) < n ln(0,9) < ln(0,0556). Diviser par ln(0,9) qui est négatif : ln(0,0556) / ln(0,9) < n < ln(0,0555) / ln(0,9). 27,4 < n < 27,5. Donc n n'est pas un entier naturel. Il n’existe aucun rang k ∈ N pour lequel vk = uk. ... .... Sujet 2. Partie A.   Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point. 1. Affirmation : La suite u définie pour tout entier naturel n par un = (−1)n / (n+1) est bornée. Vrai. n > 0, donc n+1 > 1 implique 1/(n+1) < 1 et -1/(n+1) > -1. De plus pour un entier naturel : -1 < (-1)n) < 1. Par suite : -1 / (n+1) < (-1)n /(n+1) < 1 / (n+1), n+1 étant positif. -1 < -1/(n+1) < (-1)n /(n+1) < 1 / (n+1)  < 1. La suite est bornée par 1 et par -1.  2. Affirmation : Toute suite bornée est convergente. Faux. Contre exemple :  soit la suite dfinie par un = (-1)n avec n entier naturel. Cette suite est bornée par 1 et -1, mais elle n'est pas convergente.  3. Affirmation : Toute suite croissante tend vers plus l'infini. Faux. La suite u définie sur N par un = -1 / n est croissante et converge vers zéro. 4. Soit la fonction f définie sur R par f(x)= ln(x2 + 2𝑥 + 2). Faux. Affirmation : La fonction f est convexe sur l’intervalle [−3 ; 1]. f '(x) = (2x+2) / (x2 + 2𝑥 + 2) Calcul de la dérivée seconde en posant u = 2x+2 et v = x2 + 2𝑥 + 2. u' = 2 ; v' = 2x+2. (u'v-v'u) / v2 =[2(x2 + 2𝑥 + 2)-(2x+2)2] / (x2 + 2𝑥 + 2)2. f "(x) =(-2x2-4x) / (x2 + 2𝑥 + 2)2. f " est du signe de -2x2-4x = -2x(x+2). -2x2-4x est une fonction polynome du second degré avec un coefficient dominant a négatif. Ces racines sont 0 et -2. f "(x) est positive sur (-2 ; 0] : elle est donc convexe sur cet intervalle. 5. On considère la fonction mystere définie ci-dessous qui prend une liste L de nombres en paramètre. On rappelle que len(L) renvoie la longueur, c’est-à-dire le nombre d’éléments de la liste L. def mystere (L) : M = L[0] for i in range(len(L)) : il L[i] > M : M = L[i] return M Affirmation : L’exécution de mystere([2,3,7,0,6,3,2,0,5]) renvoie 7. Vrai. M prend pour valeur le premier terme de la liste ; l'algorithme compare chaque terme de la liste à M. Si un terme est supérieur à M, il remplace M par cette valeur. L'algorithme donne la valeur maximale des termes soit 7 dans ce cas.

menu