Sujet 1.
L’espace est muni d’un repère orthonormé.
On considère :
- d
1 la droite passant par le point H(2; 3; 0) et de vecteur directeur u de coordonnées (
1;
−1;
1
)
- d
2 la droite de représentation paramétrique :
{
x= 2k − 3
; y = k ;
z= 5
où k décrit 𝐑.
Le but de cet exercice est de déterminer une représentation paramétrique d’une droite
D
qui soit perpendiculaire aux droites d
1 et d
2.
1. a. Déterminer un vecteur directeur, noté v, de la droite d
2.
Coordonnées de ce vecteur v : (2 ; 1 ; 0), c'est à dire les coefficients de k.
b. Démontrer que les droites d
1 et d
2 ne sont pas parallèles.
Les vecteurs directeurs de ces deux droites ne sont pas colinéaires : les droites ne sont pas parallèles.
c. Démontrer que les droites d
1 et d
2 ne sont pas sécantes.
Représentation paramétrique de d
1 :
x = t+x
H = t+2 ; y = -t+y
H = -t +3 ; z =t+z
H = t.
Si il existe un point commun aux deux droites :
2k-3=t+2 soit 2k = t+5 ;
-t+3 =k ; par suite : 2(-t+3)=t+5 soit t = 1 /3 et k = 8 /3.
Enfin : t = 5, ce qui est faux.
Donc les droites ne sont pas sécantes.
d. Quelle est la position relative des droites d
1 et d
2 ?
Ces droites ne sont ni sécantes, ni parallèles, elles ne sont pas coplanaires.
2. a. Vérifier que le vecteur w de coordonnées (
−1 ;
2 ;
3
) est orthogonal aux vecteurs u et v.
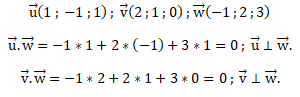 b.
b. On considère le plan P passant par le point H et dirigé par les vecteurs u et w.
On admet qu’une équation cartésienne de ce plan est :
5x + 4y − z − 22 = 0.
Démontrer que l’intersection du plan P et de la droite d
2 est le point M(3; 3; 5).
M appartient au plan :
5xM + 4yM − zM − 22 = 0.
M appartient à la droite d2 : xM= 2k − 3
; yM = k ;
zM= 5.
5(2k-3)+4k-5-22=0 ;
14 k=42 ; k =3.
xM= 2k − 3 =3
; yM = 3 ;
zM= 5.
3. Soit
D la droite de vecteur directeur w passant par le point M. Une représentation
paramétrique de
D est donc donnée par :
{ x = −r + 3
; y = 2r + 3; z = 3r + 5
où r décrit 𝐑.
a. Justifier que les droites
D et d
1 sont perpendiculaires en un point L dont on
déterminera les coordonnées.
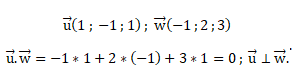
L appartient à la droite d
1 :
xL = t+2 ; yL = -t +3 ; zL = t.
L appartient à la droite D : xL = -r+3 ; yL = 2r +3 ; zL =3r+5.
t+2 = -r+3 soit t=1-r.
-t+3 = 2r+3 ; r-1+3=2r+3 soit r = -1 ; par suite t =2.
xL = 4 ; yL=1 ; zL =2.
b. Expliquer pourquoi la droite
D est solution du problème posé.
On a trouvé une droite
D perpendiculaire à d
1 et d
2.