Probabilités,
Mathématiques,
bac général Polynésie
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Sujet 1.
Les utilisateurs de vélo d’une ville sont classés en deux catégories disjointes :
- ceux qui utilisent le vélo dans leurs déplacements professionnels ;
- ceux qui utilisent le vélo uniquement pour leurs loisirs.
Un sondage donne les résultats suivants :
- 21 % des utilisateurs ont moins de 35 ans. Parmi eux, 68 % utilisent leur vélo
uniquement pour leurs loisirs alors que les autres l’utilisent dans leurs
déplacements professionnels ;
- parmi les 35 ans ou plus, seuls 20 % utilisent leur vélo dans leurs déplacements
professionnels, les autres l’utilisent uniquement pour leurs loisirs.
On interroge au hasard un utilisateur de vélo de cette ville.
Dans tout l’exercice on considère les événements suivants :
- J : « la personne interrogée a moins de 35 ans » ;
- T : « la personne interrogée utilise le vélo dans ses déplacements professionnels ».
Partie A
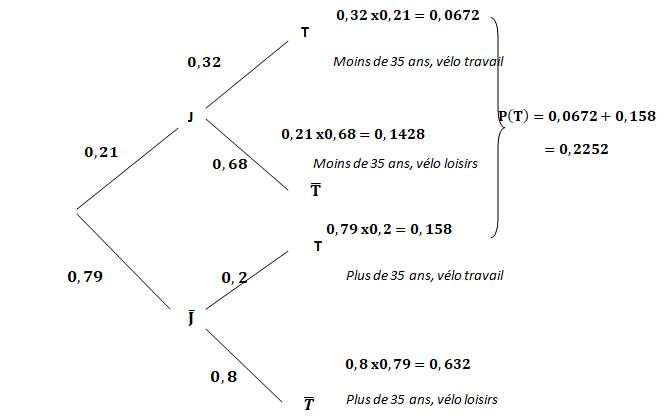
1. Calculer la probabilité que la personne interrogée ait moins de 35 ans et utilise son
vélo dans ses déplacements professionnels. On pourra s’appuyer sur un arbre
pondéré.
0,32 x0,21 = 0,0672.
2. Calculer la valeur exacte de la probabilité de 𝑇.
 3.
3. On considère à présent un habitant qui utilise son vélo dans ses déplacements
professionnels. Démontrer que la probabilité qu’il ait moins de 35 ans est 0,30 à
10 -2 près.
P T(J) =P(T n J) / P(T) =0,0672 / 0,2252 ~0,30.
Partie B.
Dans cette partie, on s’intéresse uniquement aux personnes utilisant leur vélo dans leurs
déplacements professionnels. On admet que 30 % d’entre elles ont moins de 35 ans.
On sélectionne au hasard parmi elles un échantillon de 120 personnes auxquelles on va
soumettre un questionnaire supplémentaire. On assimile la sélection de cet échantillon à
un tirage aléatoire avec remise.
On demande à chaque individu de cet échantillon son âge.
X représente le nombre de personnes de l’échantillon ayant moins de 35 ans.
Dans cette partie, les résultats seront arrondis à 10 -3 près.
1. Déterminer la nature et les paramètres de la loi de probabilité suivie par X.
La loi de X suit la loi binomiale de paramètre n = 120 ; p = 0,30.
2. Calculer la probabilité qu’au moins 50 utilisateurs de vélo parmi les 120 aient
moins de 35 ans.
p(X > 50)= 1-p(X < 49)~0,0044.( donner par la calculatrice).
|
...
|
....
|
Sujet 2. Partie A.
Chaque jour, un athlète doit sauter une haie en fin d’entraînement. Son entraîneur
estime, au vu de la saison précédente, que :
- si l’athlète franchit la haie un jour, alors il la franchira dans 90 % des cas le jour
suivant ;
- si l’athlète ne franchit pas la haie un jour, alors dans 70 % des cas il ne la
franchira pas non plus le lendemain.
On note pour tout entier naturel n :
- Rn l'événement : « L’athlète réussit à franchir la haie lors de la n-ième séance », - pn la probabilité de l'événement Rn.
On considère que p0 = 0,6.
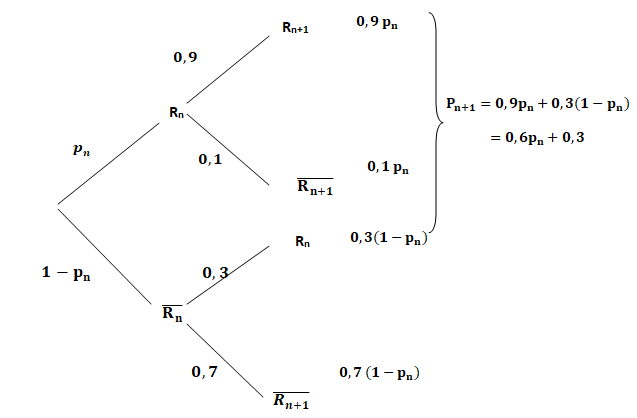
1. Soit n un entier naturel, recopier l’arbre pondéré ci-dessous et compléter les
pointillés.
2. Justifier en vous aidant de l’arbre que, pour tout entier naturel n, on a : pn+1 = 0,6 pn + 0,3.
3. On considère la suite (un
) définie, pour tout entier naturel n, par un = pn − 0,75.
a. Démontrer que la suite (un
) est une suite géométrique dont on précisera
la raison et le premier terme.
un+1 = pn+1 − 0,75 ; pn+1=0,6pn+0,3.
un+1 = 0,6pn +0,3 − 0,75 ; un+1 = 0,6pn -0,45.
un+1 = 0,6(pn-0,75) =0,6 un.
Raison q = 0,6 ; premier terme u0 =p0-0,75 = -0,15.
b. Démontrer que, pour tout entier naturel n : pn= 0,75 − 0,15 × 0,6n
.
un = 0,6n u0 = -0,15 x 0,6n.
pn = un +0,75 =0,75 -0,15 × 0,6n
.
c. En déduire que la suite (pn
) est convergente et déterminer sa limite l.
pn+1-pn = -0,15 × 0,6n+1-(-0,15 × 0,6n )=0,15 × 0,6n (1-0,6)=0,06 x0,15n.
pn+1 > pn : la suite est croissante.
0,6 < 1 ; 0,6n tend vers zéro si n tend vers plus l'infini.
pn tend vers 0,75.
La suite étant croissante et majorée, elle converge vers 0,75.
d. Interpréter la valeur de l dans le cadre de l'exercice.
Au bour d'un certain temps, l'athlète franchira les haies dans 75 % des cas.
Partie B.
Après de nombreuses séances d'entraînement, l’entraineur estime maintenant que
l’athlète franchit chaque haie avec une probabilité de 0,75 et ce indépendamment
d’avoir franchi ou non les haies précédentes.
On note X la variable aléatoire qui donne le nombre de haies franchies par l’athlète à
l’issue d’un 400 mètres haies qui comporte 10 haies.
1. Préciser la nature et les paramètres de la loi de probabilité suivie par X.
L'expérience possède deux issues : succès ( franchir la haie) ou échec ( ne pas franchir la haie).
Cette expérience est répétée 10 fois ( 10 haies à franchir) de manière indépendante.
X suit la loi binomiale de paramètre n = 10 et p = 0,75.
2. Déterminer, à 10−3 près, la probabilité que l’athlète franchisse les 10 haies.
p(X=10) = (10 10) x0,7510 x0,250~0,056.
3. Calculer P(X >9), à 10−3 près.
P(X > 9) = 1 -P(X < 8) ~0,244.
|
|