Physique chimie et mathématiques, bac STL Polynésie 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Chute verticale dans un fluide visqueux. Cet exercice propose de modéliser la chute verticale d’une bille de plomb dans une huile alimentaire. Données :  Les actions exercées par le fluide sur la bille sont modélisées par une force de frottement fluide : f = 6 p h r v dans laquelle h est la viscosité du fluide, r est le rayon de la bille et v le vecteur vitesse de la bille ;  intervalle des valeurs courantes de la viscosité h d’une huile alimentaire : entre 60 et 100 mPa·s.  Une bille de plomb de rayon r = 1,03 mm et de masse m = 0,056 g est lâchée à t = 0 s sans vitesse initiale dans une huile alimentaire . On nomme v(t) la valeur de la vitesse de la bille, exprimée en m·s-1 , à l’instant t, exprimé en seconde. L’axe Oy est orienté suivant la verticale descendante. Le pointage des positions successives de la bille permet de tracer l’évolution de sa vitesse en fonction du temps : 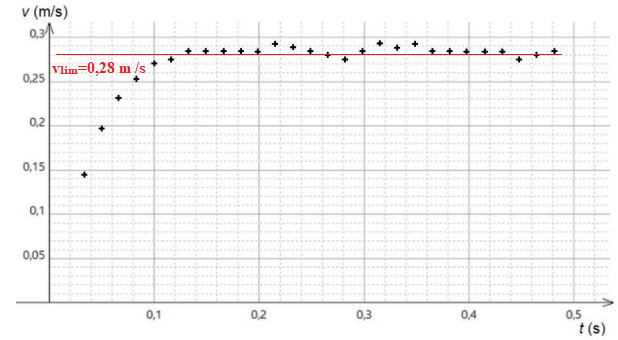1. Justifier, à partir des résultats de la figure , que la chute de la bille n’est pas une chute libre. Dans le cas d'une chute libre sans vitesse initiale la vitesse est uen fonction linéaire du temps : v = gt.  2. Estimer graphiquement la valeur de la vitesse de chute de la bille en régime permanent. Vitesse limite de chute = 0,28 m /s.  Pour la suite de l’exercice, on prendra comme valeur de la viscosité de l’huile alimentaire h = 8010-3 Pa·s. 3. En considérant le système {bille} dans le référentiel du laboratoire supposé galiléen, écrire l’expression vectorielle de la seconde loi de Newton. 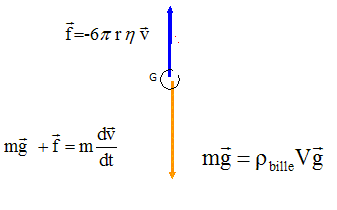4. En déduire, par projection de la deuxième loi de Newton sur l’axe (Oy), que la vitesse de chute de la bille doit vérifier l’égalité : dv /dt = - 6phr /m v + g mdv /dt = - 6phr  v +m g. Diviser par m : dv /dt = - 6phr /m v + g   Étude mathématique de la vitesse.  On souhaite déterminer une expression de la vitesse de la chute de la bille. Les données physiques de l’expérience conduisent à résoudre l’équation différentielle (E) : y ’ = - 27,7y + 9,81.  5. Déterminer l’ensemble des solutions de l’équation différentielle (E). Solution générale de y '+27,7 y = 0 : y = A exp(-27,7t) avec A une constante. Solution particulière de (E) : y = 9,81 / 27,7 =0,354. Solution générale de (E) : y = A exp(-27,7t) +0,354.  6. Montrer que l’unique solution v de l’équation différentielle (E) qui vérifie v(0) = 0 est définie par l’expression : v(t) = 9,81/ 27,7 (1-exp(-27,7 t)). Calculer la limite de v(t) en plus l'infini. v(t=0) = A exp(-27,7*0) +0,354=0. A +0,354 = 0 ; A = -0,354= -9,81 / 27,7. v(t) =y = -9,81 /27,7  exp(-27,7t) +9,81 / 27,7. v(t) = 9,81/ 27,7 (1-exp(-27,7 t)). En plus l'infini, le terme en exponentielle tend vers zéro et v(t) tend vers9,81 / 27,7 m /s. Analyse du modèle obtenu.  Dans cette expérience, la valeur de la vitesse de la bille, exprimée en m·s-1 , en fonction du temps t exprimé en s, est donnée par la fonction v définie sur [0 ; 0,5] dont l’expression est : v(t) = 0,35 × (1-exp(-27,7 t) ). 8. Vérifier la cohérence de l’ordre de grandeur de la limite obtenue à la question 7 avec celui de la vitesse en régime permanent estimée à la question 2. Proposer une justification à l’écart observé. Ecart relatif entre les deux valeurs :(0,35 -0,28) / 0,28 x100 =25 %. La bille est soumise en plus des frottements à la poussée d'Archimède, verticale vers le haut. 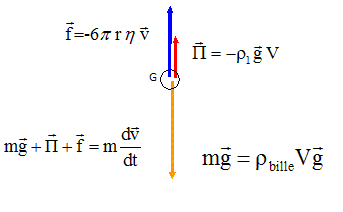 Le silicium dans les molécules organiques et dans les panneaux photovoltaïques.  Les propriétés semi-conductrices du silicium et son abondance sur Terre en font un candidat de choix pour la fabrication des panneaux photovoltaïques. Silicium et structure spatiale de molécules Le trichlorosilane est un intermédiaire dans la fabrication du silicium ultra-pur. Une représentation de Cram est donnée ci-dessous. 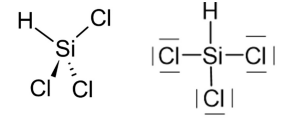1. Déterminer la géométrie autour de l’atome de silicium dans la molécule de trichlorosilane à l’aide de la théorie VSEPR. La comparer à une géométrie courante autour des atomes de carbone dans les molécules organiques. Type AX4, géométrie tétraédrique.  2. Préciser en justifiant la réponse, si la molécule de trichlorosilane est chirale. Le silicium n'est pas lié à 4 atomes différents : la molécule n'et pas chirale.  Les molécules organiques contenant du silicium sont aussi utilisées pour synthétiser des molécules d’intérêt biologique. La molécule ci-dessous, notée A, permet la fabrication au laboratoire d’une phéromone naturelle. 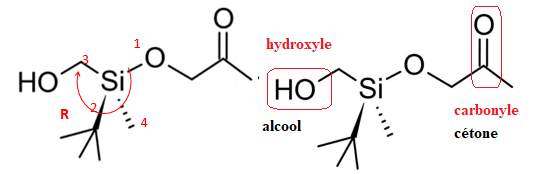3. Repérer deux groupes caractéristiques de la molécule, les recopier dans la copie et donner le nom de la fonction chimique associée à chacun d’entre eux. 4. Donner la définition d’un atome de carbone asymétrique. Carbone lié à 4 atomes ou groupe d'atomes différents. 5. Appliquer les règles de Cahn, Ingold et Prelog aux quatre groupes d’atomes portés par l’atome de silicium dans la molécule A pour leur classement par ordre de priorité.  6. Déduire la configuration absolue de l’atome de silicium de la molécule, avec la même méthode que celle utilisée pour un atome de carbone. Structure cristalline des cellules en silicium d’un panneau photovoltaïque. Données : dimensions de la cellule photovoltaïque : 9,7 cm x 7,6 cm.  Différents types de cellules en silicium sont utilisées pour fabriquer des panneaux photovoltaïques :  - les cellules monocristallines (sc-Si) dont le rendement commercial des modules se situe entre 13 et 21 %. Cette technologie est avantageuse, mais présente un coût élevé en raison du prix des matériaux et de la quantité d'énergie requise pour leur fabrication ; - les cellules polycristallines (mc-Si) dont le coût de fabrication est plus avantageux mais qui présentent un rendement entre 11 et 18 % plus faible que les cellules monocristallines. Environ 57 % des panneaux photovoltaïques vendus dans le monde se composaient de cellules mc-Si en 2011 ; - les cellules au silicium amorphe (a-Si) ne contenant du silicium que sur une épaisseur d'environ 1 µm. Le caractère amorphe, c’est-à-dire désordonné des atomes de silicium dans ces cellules entraine des rendements plus faibles, compris entre 6 et 8 %. Jusqu'en 2000, cette technologie a principalement été destinée à alimenter de petits appareils électroniques, comme des montres ou des calculatrices. D’après le site Futura-Sciences.  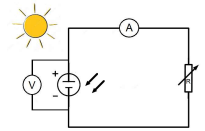Dans le cadre de l’étude expérimentale d’un panneau photovoltaïque, on mesure la tension U (en V) aux bornes du panneau photovoltaïque et l’intensité I (en A) du courant qu’il délivre lorsqu’il alimente une résistance variable R branchée à ses bornes grâce au dispositif expérimental ci-dessous : Les mesures obtenues sont intégrées dans un programme écrit en langage Python pour déterminer la puissance électrique délivrée, notée Pé, dans le circuit par le panneau. Une capture d’écran d’un extrait du programme est donnée ci-après. 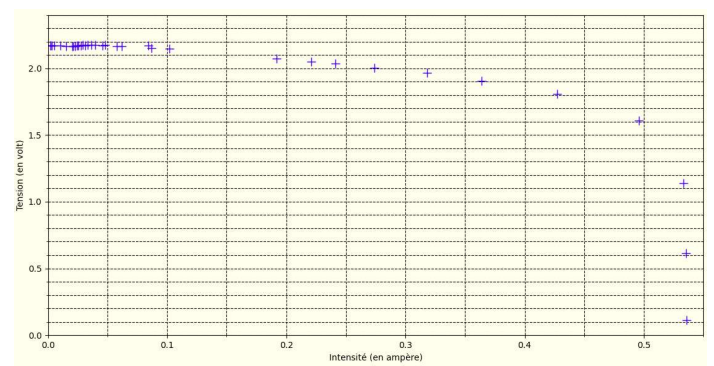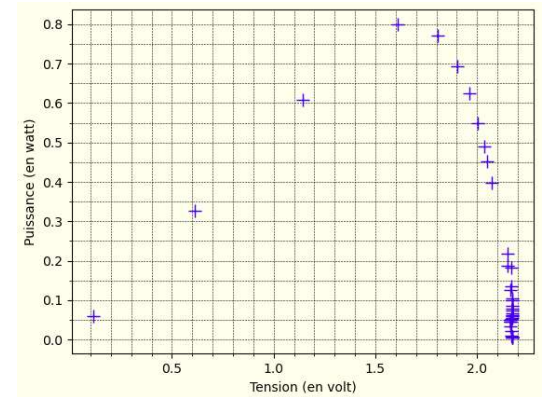Le programme trace l’évolution de la tension U en fonction de l’intensité I puis l’évolution de la puissance P en fonction de la tension U aux bornes du générateur. 7. Justifier que le panneau solaire n’est pas une source idéale de tension. La tension U n'est pas constante, elle dépend de l'intensité. 8. Déterminer, parmi les valeurs mesurées de la tension U et de l’intensité I, celles pour lesquelles la puissance délivrée par le panneau solaire est maximale. U = 1,6 V et I = 0,5 A. P = U x I = 1,6 x0,5 = 0,8 W.  9. Recopier sur la copie la ligne de code du programme écrit en langage Python qui calcule les valeurs successives de la puissance électrique libérée P. P= [U*I] 10. Sachant que les mesures ont été réalisées sous un éclairement énergétique de 900 W·m–2, déterminer la nature probable de la cellule photovoltaïque (cellule monocristalline (sc-Si), cellule polycristalline (mc-Si) ou cellule au silicium amorphe (a-Si)). Surface de la cellule S = 9,7 x 7,6 =73,72 cm2 = 7,372 10-3 m2. Puissance solaire reçue : 900 x 7,372 10-3 ~6,6 W. Rendement : 0,8 / 6,6 x100 ~12 %. ( cellule polycristalline) ... .... Exercice 3. La fonction 𝑓 est définie sur [0; +∞[ par : f(x) = x exp(0,02x) − 10 000. 1. Déterminer la limite de f(x) en plus l'infini. exp(0,02x) tend vers plus l'infini ; par produit des limites f(x) tend vers plus l'infini.  2. On note f ' la fonction dérivée de f sur [0; +∞[. Justifier que pour tout nombre réel 𝑥 ≥ 0, f '(x) = (0,02𝑥 + 1)exp(0,02x) On pose u = x et v = exp(0,02x) ; u' = 1 ; v' = 0,02 exp(0,02x). u'v+v'u = exp(0,02x) +0,02 x exp(0,02x) = f '(x) = (0,02𝑥 + 1)exp(0,02x).  3. En déduire le sens de variation de 𝑓 sur [0; +∞[ . exp(0,02x) >0 ; 0,02x+1 > : la dérivée est strictement positive et f(x) est strictement croissante.  4. L’affirmation suivante est-elle vraie ou fausse ? Justifier. « Tout nombre réel x, compris entre 0 et 1000, a une image négative par f. » f(0) = -10 000 ; f(1000) ~4,85 1011. L'affirmation est fausse.  5. Quatre fonctions A, B, C et D sont écrites dans le même programme Python ci-dessous. Laquelle de ces quatre fonctions permet de déterminer la plus petite valeur entière dont l’image par f est positive ? def B():  n=0 f = –10000  while f <0:  n=n+1  f =n *exp(0.02 * n) –10000  return n Étude d’une pile Daniell.  Une pile Daniell est constituée d'une lame de zinc plongée dans une solution contenant un volume V0 = 20 mL d’une solution de sulfate de zinc (Zn2+(aq) + SO4 2- (aq)) de concentration C0 = 1,0 10-2 mol·L-1 et d'une lame de cuivre plongée dans une solution contenant un volume V0 = 20 mL de solution de sulfate de cuivre (Cu2+(aq) + SO4 2- (aq)) de concentration C0 = 1,0 10-2 mol·L-1. Les deux solutions sont reliées par un pont salin contenant une solution de nitrate d’ammonium (NH4 + (aq) + NO3 - (aq)). Un voltmètre est branché aux bornes de la pile pour mesurer la valeur de la tension à vide U0 lorsque la pile ne débite pas de courant électrique. Le voltmètre mesure une tension à vide positive : U0 = + 1,102 V. 1. Préciser, en justifiant la réponse, la polarité de chaque électrode. Le voltmètre donne une valeur positive : la borne COM est reliée à l'électrode négative, le zinc. Par la suite, on remplace le voltmètre par un ampèremètre en série avec une résistance électrique.  2. Écrire les équations de demi-réaction électroniques se produisant à l’anode et à la cathode. En déduire la réaction d’oxydoréduction modélisant la transformation chimique au sein de la pile. Oxydation du zinc à l'anode négative Zn(s) --> Zn2+aq + 2e-. Réduction des ion Cu2+ : Cu2+aq + 2e- --> Cu(s). Cu2+aq + Zn(s)--> Cu(s) +Zn2+aq.  3. Donner le sens de déplacement des ions ammonium NH4 + (aq) et des ions nitrate NO3 – (aq) dans le pont salin. Il apparaît des ions positifs à la cathode ( à gauche). Les ions nitrate migrent vers ce compartiment afin que la solution reste électriquement neutre. Il disparaît des ions positifs à l'anode ( à droite). Les ions ammonium migrent vers ce compartiment afin que la solution reste électriquement neutre. La masse de la lame de cuivre est m(Cu) = 62,8 g et celle de la lame de zinc est m(Zn) = 50,2 g. 4. Déterminer le réactif limitant de la réaction. M(Zn) = 65,4 g / mol ; n(Zn) = 50,2 / 65,4 ~0,77 mol. n(Cu2+aq) =C0V0 =0,010 x20 / 1000 = 2,0 10-4 mol ( en défaut) 5. En déduire la capacité Q de la pile Daniell. Commenter la valeur obtenue. Quantité de matière d'électrons : 2 n(Cu2+aq) =4,0 10-4 mol Q = 4,0 10-4 *96500 ~39 C ou 39 / 3600 =1,1 10-2 Ah ou 11 mAh( valeur très faible). Étude d’une pile alcaline. 6. Identifier en justifiant la réponse, le réactif limitant de la pile alcaline. Pour éviter la polarisation de la pile en fin de vie, on utilise plus de dioxyde de manganèse qu'il n'est nécessaire pour réagir avec la totalité du zinc. Le zinc est le réactif limitant.  7. Identifier l’oxydant et le réducteur dans ce type de pile. Le zinc s'oxyde, c'est le réducteur. Le dioxyde de manganèse se  réduit, c'est l'oxydant. Une pile alcaline AA du commerce de type Power+ est reliée à une résistance de 10 ohms. L’intensité est mesurée à l’aide d’un ampèremètre. La courbe de l’évolution de l’intensité I débitée au cours du temps est donnée ci-dessous. 8. On considère qu’une chute brutale de l’intensité correspond à une pile déchargée. Déduire des mesures effectuées la valeur de la durée de fonctionnement de la pile dans ces conditions d’utilisation. 27 heures.  9. En s’appuyant sur le graphique, proposer une valeur de l’intensité moyenne délivrée par la pile Power+, puis estimer la valeur de sa capacité, notée Q. Commenter le résultat. Imoyen ~100 mA. Q = I Dt = 100 x27 = 2700 mAh, valeur très importante. Alimentation d’une voiture radiocommandée et étude des performances.  Une voiture télécommandée, de type voiture de cascade tout terrain, est alimentée par un bloc de 6 piles alcalines AA Power+ étudiées précédemment. La tension à vide mesurée aux bornes du bloc d’alimentation vaut U0 = 9,23 V. La valeur de l’intensité du courant fourni par le bloc d’alimentation lorsque la voiture est en fonctionnement est I = 600 mA. Pour la suite de l’exercice, on prendra comme valeur pour la capacité du bloc d’alimentation : QB = 10 000 C. Les piles étant branchées en série, la capacité du bloc correspond à la capacité d’une seule pile.  10. Déterminer la valeur de la durée d’utilisation maximale attendue de la voiture télécommandée. Commenter le résultat. Capacité des 6 piles : 60 000 C. Durée d'utilisation Q / I = 60 000 /0,600 =1,0 105s ou environ 28 heures ( Valeur assez importante).  Les performances de la voiture sont testées sur une route horizontale et rectiligne. La voiture est initialement arrêtée et parcourt une distance d = 9,0 m au bout d’une durée Dt = 12 s. On suppose que l’énergie électrique provenant des piles est intégralement convertie en énergie cinétique pour faire avancer la voiture. 11. Exprimer l’énergie électrique transférée par les piles au cours du test de performance en fonction de Dt, I, et U0. En déduire la valeur de la vitesse de la voiture en exploitant ce transfert d’énergie et commenter la valeur obtenue. Masse de la voiture m = 0,741 kg. Energie électrique : I U0 Dt = 0,600 x 9,23 x12 =66,45 J. Energie cinétique de la voiture ½mv2 =66,45 ; v2 = 2 x66,45 / 0,741 =179,36 ; v =13,4 m /s ou 48 km / h ( valeur importante pour une petite voiture).

menu