Tir à l'arc à la perche verticale, bac Nlle Calédonie 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Le jeu consiste à abattre des cibles, appelées « oiseaux », situées en haut d'une perche mesurant 30 mètres, les premières cibles se trouvant à 25 mètres du sol. L'archer se positionne au bas de la perche afin d'abattre le plus d'oiseaux possibles. Les oiseaux rapportent des points selon leur position sur la perche. Pour être susceptible de marquer des points l’archer doit faire en sorte que la flèche atteigne, au niveau de la perche, une hauteur comprise entre 25 et 30 m. 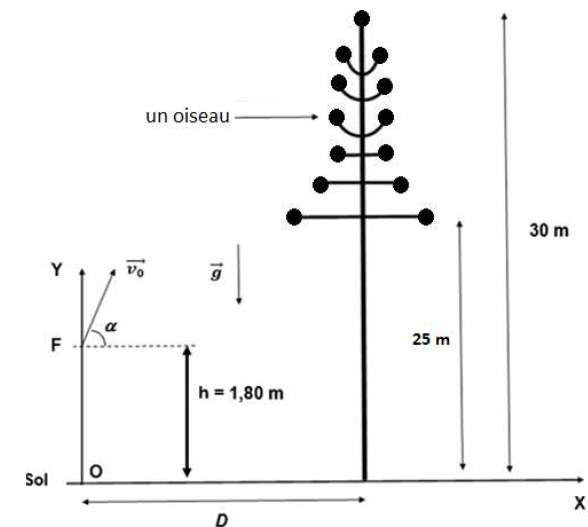Dans cet exercice, on s’intéresse au mouvement de la flèche assimilée à un point matériel de masse m = 100 g dans le référentiel terrestre supposé galiléen. Les frottements seront négligés. La situation est représentée sur la figure 2 ci-dessous, sans souci d’échelle. Partie A : Étude énergétique d’un tir vertical. L’archer tire une flèche verticalement et se demande si celle-ci dépassera le haut de la perche situé à 30 m. On appelle H la hauteur maximale atteinte par la flèche à l’instant t = tH. À l’instant initial 𝑡 = 0, l’archer lance sa flèche du point F. Le centre de gravité de la flèche F est situé à une hauteur h = 1,80 m du sol. Un capteur mesure la vitesse initiale v0 de la flèche et indique v0 = 25,0 ± 0,5 m ∙ s-1. On néglige tous les frottements. L’origine de l’énergie potentielle de pesanteur est prise au niveau du sol. A.1. Donner l’expression de l’énergie mécanique Em(0) de la flèche à 𝑡 = 0 en fonction de h, m, g et v0. Em(0) = mgh +½mv02. A.2. Donner l’expression de l’énergie mécanique Em(tH) de la flèche à t=tH en fonction de m, g et H. Em(tH) = mg H. A.3. En déduire que H = h +½v02 /g. Conservation de l'énergie mécanique : mgh +½mv02 = mg H. h +½v02 / g=  H.. L’incertitude-type u(H) sur H se calcule avec la relation : u(H) = [(u(h))2+(v0 / g)2(u(vo))2]½. A.4.1. Calculer H en vous appuyant sur la question A.3. H =1,80 +0,5 x25,02 / 9,8 =33,7 m. A.4.2. Évaluer u(H) sachant que u(h) = 0,01 m, puis donner un encadrement de la valeur de H. u(H) = [(0,01)2+(25 / 9,8)2(0,5))2]½= [10-4+1,63]½=1,3 m A.4.3. Indiquer si la flèche dépasse le haut de la perche. Justifier. H = 33,7 ±1,3 m. La flèche dépasse le haut de la perche. ... .... Partie B : Étude de la trajectoire de la flèche lors d’un tir visant le mat L’archer situé à une distance D = 5 m de la base de la perche essaie maintenant d’atteindre les oiseaux situés sur le mat en tirant la flèche avec un angle de tir a = 80°. À l’instant initial t = 0 s, le centre de gravité de la flèche F est situé à une hauteur h = 1,80 m du sol. La vitesse initiale est notée v0 et a pour valeur  25,0 m ∙ s-1. B.1. Faire un bilan des forces s’exerçant sur la flèche. Les frottements étant négligés, la flèche n'est soumise qu'à son poids. B.2. En utilisant la deuxième loi de Newton, déterminer les coordonnées ax (t) et ay (t) du vecteur accélération de la flèche. ax(t) =0 ; ay(t) = -g. B.3. Montrer que les équations horaires du mouvement de F ont pour expression : x(t) = v0 cos a t ; y(t) = -½gt2 + v0 sin a t +h. La vitesse est une primitive de l'accélération. vx(t) = v0 cos a ; vy(t) = -gt +v0 sin a . La position est une primitive de la vitesse et la position initialea pour coordonnées ( 0 ; h). x(t) = v0 cos a t ; y(t) = -½gt2 + v0 sin a t +h.  B.4. Montrer que l'équation de la trajectoire 𝑦(x) de F peut s’écrire : 𝑦(𝑥) = −½gx2 /(v02cos2a) +tan a x +h. t = x(t) / (v0 cos a). Repport dans y(t) : 𝑦(𝑥) = −½gx2 /(v02cos2a) +tan a x +h. B.5. Indiquer, en justifiant, si son tir peut lui permettre de marquer des points. y(D) =−½gD2 /(v02cos2a) +tan a D +h. y(D) = -4,9 x52 /((25xcos80)2)+5 tan 80 +1,80 = -6,5 +28,35 +1,80 =23,7 m. Cette valeur étant inférieure à 25 m, aucun oiseau n'est atteint , donc aucun point n'est marqué.

menu