Partie A - Étude de la capacité du
capteur en fonction de l’humidité.
Le capteur d’humidité comprend un condensateur plan pouvant être
schématisé de la manière
suivante :

La capacité d’un tel condensateur est exprimée par la relation suivante
: 𝐶 =
e0 er S /
l.
.
Les grandeurs physiques apparaissant dans cette équation sont
respectivement :
𝐶 la capacité du condensateur en farads (F) ;
•
e0 la permittivité du vide, l’une des constantes fondamentales de la
physique ;
•
er la permittivité relative du milieu, caractéristique variable d’un
environnement à un autre
(grandeur sans unité) ;
• 𝑆 la surface des armatures du condensateur plan qui se font face ;
•
l la distance entre les deux armatures.
Le principe du capteur réside dans le fait que la capacité du
condensateur change en fonction de
la proportion d’eau présente dans le sol.
A.1. La permittivité de l’air est
er,air = 1,0 alors que celle de
l’eau est
t er,rau = 80. En déduire,
parmi l’air et l’eau, le milieu pour lequel la capacité du condensateur
sera la plus grande.
Dans l'eau la capacité sera la plus grande.
A.2. Justifier alors que, pour une même charge électrique 𝑞 portée par
une armature du condensateur, la tension électrique aux bornes de celui-ci est plus
faible quand il est plongé dans l’eau que quand il est laissé à l’air libre.
U = q / C. Tension et capacité sont inversement proportionnelles, à q constant.
Partie B - Étude de la charge d’un condensateur
Le capteur est connecté à un microcontrôleur. Dès que le
microcontrôleur est mis en route, cela déclenche la charge du
condensateur qui compose le capteur alors que ce dernier est encore
dans l’air.
Le système est modélisé par le circuit représenté ci-après comportant un condensateur de capacite 𝐶
air en série avec un générateur idéal de tension, ayant pour tension à ses bornes 𝐸, et une résistance de valeur 𝑅.
On considère que le condensateur est initialement déchargé.
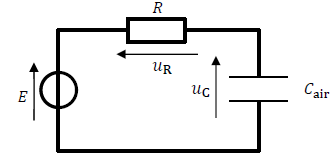 B.1.
B.1. Établir, pour le circuit, la relation entre 𝐸, 𝑢
𝑅 (𝑡) et 𝑢
𝐶 (𝑡).
Additivité des tensions : E = u
R(t) + u
C(t).
B.2. Donner la
relation mathématique entre l’intensité du courant 𝑖(𝑡) et la charge
électrique 𝑞(𝑡) qui traverse une portion de circuit. Préciser les
unités de chacune des grandeurs.
i = q(t) / dt = C du
C(t) / dt.
i : ampère ; q(t) : coulomb ; t : seconde.
B.3. Montrer alors que l'équation différentielle qui régit l’évolution de la tension 𝑢
𝐶 aux bornes du condensateur est :
E = Ri(t) +
uC(t) = RCair duC(t) / dt +uC(t).
duC(t) / dt +uC(t) / (RCair) = E / (RCair). (E)
B.4.1. Montrer que uC(t) = 𝐸 × (1 − exp(- t / t) est solution de l’équation différentielle à condition que
t = 𝑅 × 𝐶air .
duC(t) / dt = -E / t exp(- t / t) ; repport dans (E).
-E / t exp(- t / t) +E / t (1 − exp(- t / t) = E est vérifiée quel que soit t.
B.4.2. Nommer le produit des grandeurs 𝑅 et 𝐶air .
RCair : constante de temps.
B.5. Montrer qu’une fois avoir attendu un temps suffisamment long, la charge du condensateur vaut 𝑄chargé = 𝐶air × 𝐸.
Au bout d'un temps suffisamment long, le terme en exponentielle est nul : uC(t) = 𝐸.
Qchargé = Cair uC(t) = Cair E.