Fonctions, Mathématiques, bac général Amérique du Nord 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Sujet 1. On considère la fonction f définie sur R par : f (x) = e 3x −(2x +1)ex.  Le but de cet exercice est d’étudier la fonction f sur R. Partie A - Étude d’une fonction auxiliaire On définit la fonction g sur R par : g(x) = 3e2x −2x −3.  1. a. Déterminer la limite de la fonction g en -oo. En moins l'infini : e2x tend vers zéro ; -2x tend vers plus l'infini. Par suite g(x) tend vers plus l'infini.  b. Déterminer la limite de la fonction g en plus l'infini. g(x) = e2x(3-2x / e2x-3 /e2x) ; -2x / e2x et -3 /e2xtendent vers zéro. e2x tend vers plus l'infini ; g(x) tend vers plus l'infini.  2. a. On admet que la fonction g est dérivable sur R, et on note g ′ sa fonction dérivée. Démontrer que pour tout nombre réel x, on a g ′ (x) = 6e2x −2. g'(x) = 3*2e2x-2 = 6e2x −2 = 2(3e2x-1). b. Étudier le signe de la fonction dérivée g ′ sur R. g'(x) =0  si 3e2x-1=0 ; e2x = 1 /3 ; 2x = ln(1 /3) ; x = 0,5 ln(1/3) = -0,5 ln(3). Si x > -0,5 ln(3), g'(x) >0 et g(x) est croissante. Si x < -0,5 ln(3), g'(x) < 0 et g(x) est décroissante.  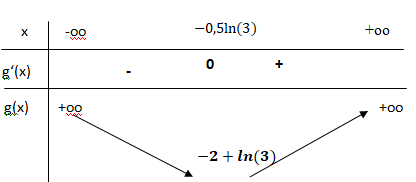c. En déduire le tableau de variations de la fonction g sur R. Vérifier que la fonction g admet un minimum égal à ln(3)−2. 3. a. Montrer que x = 0 est solution de l’équation g(x) = 0. g(0) =3e0 −0 −3=3-3=0. DDonc x =0 est solution de l'équation g(x)=0. b. Montrer que l’équation g(x) = 0 admet une deuxième solution, non nulle, notée a, dont on donnera un encadrement d’amplitude 10−1 . -0,5ln(3) < 0. Sur ]-0,5ln(3) ; +oo[, g est strictement croissante. g(0)=0, donc x=0 est le seule solution de l'équation g(x)=0. Sur ]-oo ; -0,5ln(3) [, g est continue ( car elle est dérivable) et strictement décroissante. Zéro est comprise entre moins l'infini et g(-0,5 ln(3))=ln(3) -2 < 0. D'après le corollaire du  théorème des valeurs intermédiaires, l'équation g(x) =0 admet une solution uique sur cet intervalle. La calculatrice conduit à : -1,5 < a < -1,4. 4. Déduire des questions précédentes le signe de la fonction g sur R. g est strictement positive sur ]-oo ; a[ et sur ]0 ; +oo[. g est strictement négative sur ]a ; 0[.  Partie B - Étude de la fonction f 1. La fonction f est dérivable sur R, et on note f ′ sa fonction dérivée. Démontrer que pour tout nombre réel x, on a f ′ (x) = e x g(x), où g est la fonction définie dans la partie A. f (x) = e 3x −(2x +1)ex ; g(x) = 3e2x −2x −3. Dérivée du produit (2x-1) ex. On pose u = 2x+1 et v =ex ; u' =2 ; v' =ex. u'v+v'u = 2ex+(2x+1)ex =ex(2x+3). f '(x) =3e3x -ex(2x+3)= ex( 3e2x-2x-31= e x g(x), 2. En déduire alors le signe de la fonction dérivée f ′ puis les variations de la fonction f sur R. ex est strictement positif ; f ' a le signe de g(x). f est strictement croissante sur ]-oo ; a[ et sur ]0 ; +oo[. f est strictement décroissante sur ]a ; 0[.  3. Pourquoi la fonction f n’est-elle pas convexe sur R? Expliquer. Si la fonction f était convexe sur R, alors sa dérivée f ' serait croissante sur R. Or f ' est à valeurs positives sur ]-oo ; a[ et à valeurs négatives sur ]a ; 0[. f ' n'est pas croissante sur R et f n'est pas convexe sur R. ... .... Sujet 2.  Partie A Le plan est muni d’un repère orthogonal. On considère une fonction f définie et dérivable sur R. On note f ′ sa fonction dérivée. On donne ci-dessous la courbe représentative de la fonction dérivée f ′ . Dans cette partie, les résultats seront obtenus par lecture graphique de la courbe représentative de la fonction dérivée f ′ . Aucune justification n’est demandée. 1. Donner le sens de variation de la fonction f sur R. On utilisera des valeurs approchées si besoin. f '(x) > 0 sur ]-oo ; 0,4[ ; f est strictement croissante sur cet intervalle. f '(x) > 0 sur ]2,6 ; +oo[ ; f est strictement croissante sur cet intervalle. f '(x) < 0 sur ]0,4 ; 2,6[ ; f est strictement décroissante sur cet intervalle. 2. Donner les intervalles sur lesquels la fonction f semble être convexe. f ' est croissante sur  ]-oo ; -1[ et sur ]2,6 ; +oo[ : f est convexe sur ces intervalles. Partie B On admet que la fonction f de la partie A est définie sur R par f (x) = ( x2 −5x +6 ) ex . On note C la courbe représentative de la fonction f dans un repère. 1. a. Déterminer la limite de la fonction f en +oo. Quand x tend vers plus l'infini : x2 −5x +6 et ex tendent vers plus l'infini ; f(x) tend vers plus l'infini. b. Déterminer la limite de la fonction f en −oo. Quand x tend vers moins l'infini : x2 −5x +6 tend vers plus l'infini ; ex tend vers zéro. Par produit des limites f(x) tend vers zéro. 2. Montrer que, pour tout réel x, on a f ′ (x) = ( x 2 −3x +1 ) e x . On pose u =x2 −5x +6 et v = ex ; u' = 2x-5 ; v' = ex. u'v +  v'u = ex(2x-5 +x2 −5x +6) = ( x 2 −3x +1 ) e x .  3. En déduire le sens de variation de la fonction f . ex est strictement positif. Le signe de f '(x) est celui de x 2 −3x +1. Solutions de x 2 −3x +1 = 0. Discriminant : (-3)2 -4 =5. x1 = (3+5½) / 2 ; x2 = (3-5½) / 2.  4. Déterminer l’équation réduite de la tangente (T ) à la courbe C au point d’abscisse 0. y = f '(0) (x-0)+f(0). f ′ (0) = ( 0 2 −3*0 +1 ) e 0 = 1. f(0) =( 02 −5*0 +6 ) e0 =6. y =x+6.  On admet que la fonction f est deux fois dérivable sur R. On note f ′′ la fonction dérivée seconde de la fonction f .  On admet que, pour tout réel x, on a f ′′(x) = (x +1)(x −2)ex . 5. a. Étudier la convexité de la fonction f sur R. Il faut étudier le signe de f "(x).  b. Montrer que, pour tout x appartenant à l’intervalle [−1 ; 2], on a f (x) < x +6. Sur cet intervalle la fonction est concave ; la courbe C est en dessous de ces tangentes. Zéro appartient à [-1 ; 2], donc pour tout réel  de  cet intervalle, f(x) < x+6.

menu