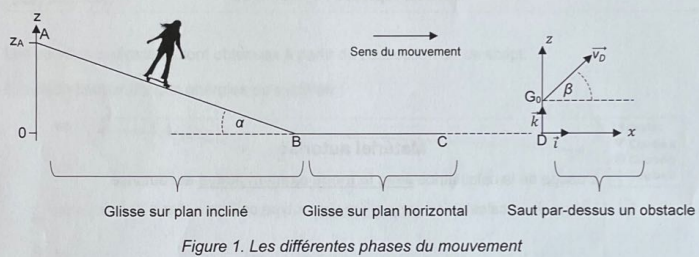
Le STREET, une pratique olympique, bac général Amérique du Nord 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . .. . . . . .. .. ...... ... Masse du système m = 75,0 kg. A. Glisse sur le plan incliné. Il s'élance sans vitesse initiale du point A le long de la pente pour rejoindre le point B. Les frottements de l'air seront négligés. Les frottement des roues sur la piste sont modélisés par une force F. 1. Nommer en justifiant l'es énergies correspondantes. 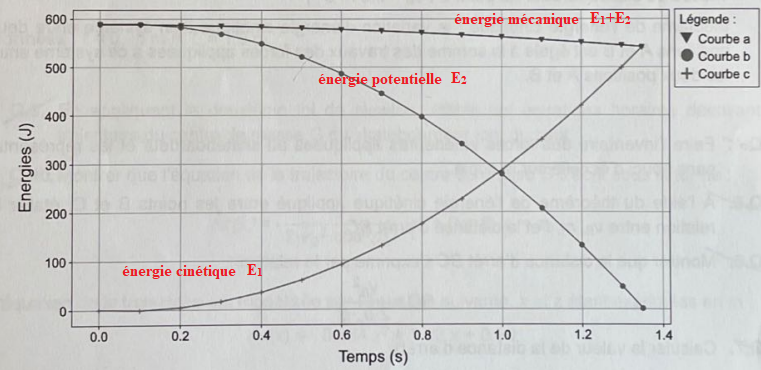L'énergie cinétique initiale est nulle puis elle augmente. L'énergie potentielle est maximale au départ puis elle diminue. L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle.. 2. Interpréter l'évolution de l'énergie mécanique. L'énergie mécanique diminue du travail des frottements. 3. Déterminer la vitesse en B. Energie cinétique en B : 550 J. 550 = ½mvB2. vB = (2 x550 / 75)½ =3,83 ~3,8 m /s. Phase du mouvement horizontal. Le skateboardeur glisse pour s'arrêter en C. Les frottements de l'air sont négligés.  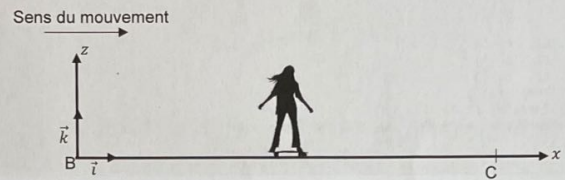Il est soumis à une force de frottement f qui s'oppose au mouvement. Coefficient de frottement cinétique µc = f / R = 0,040. f : force de frottement et R norme re la réaction normale du plan. 4. Faire l'inventaire des forces et les représenter. Poids, verticale vers le bas, valeur mg. Action normale du plan, verticale vers le haut. Force de frottement, sens contraire du déplacement. 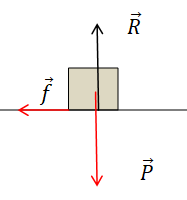5. à 7 Etablir la relation entre vB, m, f et la distance d'arrêt BC. Calculer BC. P et R, normales au déplacement, ne travaillent pas. Travail résistant de f : - f BC. Théorème de l'énergie cinétique entre B et C : 0 -½mvB2 = - f BC. BC = ½mvB2  / f avec f = µcmg. BC =vB2  /(2 µc g). BC = 3,82 / (2 x 0,040 x9,81)=18,4 ~18 m. Plus les roues sont dures, plus les frottements sont faibles. 8. Comment évolue la distance d'arrêt suite à un changement de roues ( roue moins dures de même géométrie). Les frottements seront plus importants, c'est à dire µc augmente et la distance d'arrêt diminue. ... .... Etude du saut et photographie. En arrivant à la verticale du point D, il déclenche un saut par dessus un obstacle de longueur L, de faible hauteur. Le centre de masse du skateboardeur a pour coordonnées z0 = 0,80 m et x0 = 0 et sa vitesse est v0. L'action de l'air est négligeable. l = 0,70 m et L = 1,0 m. 9. Etablir les équations horaires décrivant la trajectoire du centre de masse G lors du saut. Le pilote n'est soumis qu'à son poids. La seconde loi de Newton conduit à ax =0 et az = -g. La vitesse est une primitive de l'accélration : vx = A ; vz = -gt + B, avec A et B des constantes. A t=0 : vx = A =vD cos ß ; vz = B =vD sin ß . La position est une primitive de la vitesse : x = vD cos ß t +C ; z = -½gt2 +vD sin ß t + D avec C et D des constantes. A t=0 : x = 0 = C ; z = z0 = D. x(t) = vD cos ß t ; z = -½gt2 +vD sin ß t +z0. 10. Montrer que la trajectoire du centre de masse est : z(x) = -g / (2 vD2 cos2ß) x2 +tan ß x + z0. t = x / (vD cos ß) ; repport dans z : z(x) = -g / (2 vD2 cos2ß) x2 +tan ß x + z0. L'équation de la trajectoire est modélisée par : z(x) = -0,894 x2 +1,22 x +0,80. 11. Calculer la valeur de x lorsque le skateboardeur retrouve l'altitude initiale z0 = 0,8 m. -0,894 x2 +1,22 x +0,80= 0,80. -0,894 x2 +1,22 x =0 Solutions x = 0 et x =1,22 / 0,894  = 1,36 m ~1,4 m. 12. L'obstacle est-il franchi ? L + l = 1,7 m, l'obstacle n'est pas franchi. Un photographe  souhaite photographier le skateboardeur pendant la saut précédent. L'appareil est équipé d'un flash. Les éléments essentiel d'un flash sont le condensateur et le tube néon émettant le flash lorsque le condensateur se décharge. On donne le schéma simplifié du fonctionnement du flash. Le déclenchement du flash provoque le basculement de l'interrupteur en position 2. 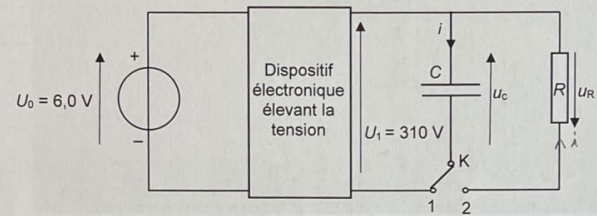13. Montrer que l'équation différentielle modélisant l'évolution de la tension uc lors de la décharge s'écrit : duc /dt + uc / t = 0. uc + uR =0. uR = R i avec i = dq/dt = C duc /dt. uc + RCduc/dt =0. On pose t = RC. 14. Vérifier que la solution de cette équation est u(t) = A exp(-t / B). Exprimer A et B en fonction des paramètre du circuit. u '(t) =-A / B exp(-t / B). Repport dans l'équation : A exp(-t / B)- RC * A / B exp(-t / B) =0 Cette égalité est vérifiée si : B = RC.. A t=0; uc = U1 = A. 15. Montrer que t est homogène à un temps. -t / t est sans dimension, donc t est homogène à un temps. On fournit la courbe de décharge. 16. Déterminer t. 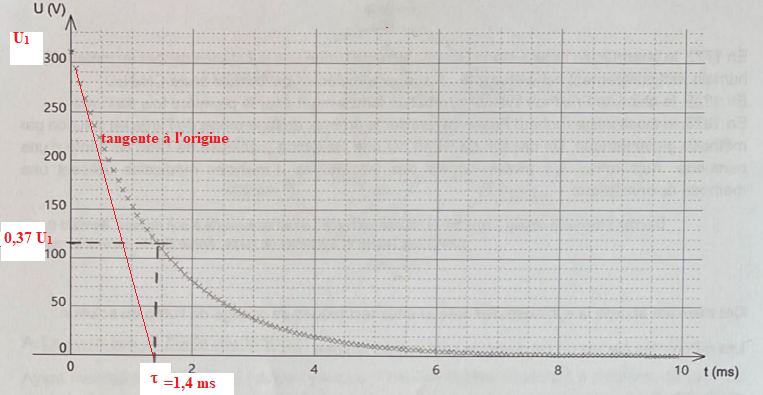La durée qui sépare le déclenchement de la photographie et la prise  réelle de la photo est d'environ 5t soit 7,5 ms. La photo est déclenchée lorsque le skateboardeuur passe en D.  Le saut est décomposé en trois étapes : avant l'obstacle, au dessus de l'obstacle, après l'obstacle. On donne vD = 3,5 m /s et ß = 50,7°. 17. Quelle est l'étape photographiée ? x(t) = vD cos ß t ; x(t = 7,5 10-3) =3,5 cos 50,7 x7,5 10-3 =0,017 m. Cette valeur étant inférieure à l = 0,70 m, l'étape 1, avant l'obstacle, est photographiée.

menu