Physique chimie et mathématiques, bac STL métropole 2023.
mécanique, électrolyse, acide benzoïque.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
Exercice 1. 5 points
  Lors d’une séance expérimentale, un binôme d’élèves réalise la vidéo du mouvement d’une voiture miniature de masse m = 0,040 kg, en roue libre. L’objectif de l’expérience est de déterminer l’intensité F de l’ensemble des forces de frottement qui s’exercent sur la voiture et la distance d parcourue avant l’arrêt. Les forces de frottement sont supposées constantes. L’étude est menée dans le référentiel du sol supposé galiléen. Le mouvement de la voiture est rectiligne et s’effectue selon un axe horizontal (Ox) fixe.
L’analyse de la vidéo obtenue par le binôme d’élèves, au moyen d'un logiciel de pointage, permet d'obtenir le graphe de l’évolution de la position x du centre de masse G de la voiture au cours du temps.


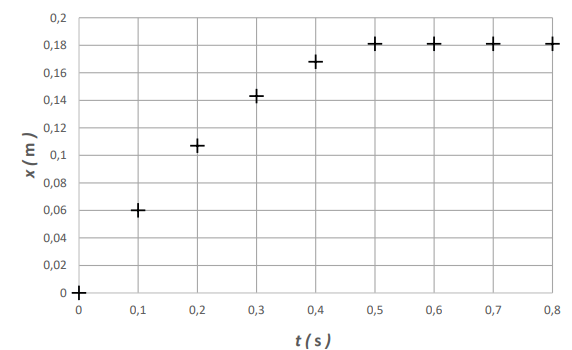1. Décrire l’évolution (croissante, décroissante…) de la vitesse de la voiture au cours du temps.
Les distances parcourues pendant des durées constantes diminuent au cours du temps : la vitesse décroît.
 2. En utilisant la figure, calculer la vitesse moyenne de la voiture entre les instants t0 = 0 et t = 0,1 s.
0,06 / 0,1 = 0,6 m /s.
Le nuage expérimental de points peut être modélisé par une fonction polynomiale sur l'intervalle de temps [0 ; 0,50], le temps étant exprimé en secondes. On rappelle que la position x est exprimée en mètres. Cette fonction, notée x, a pour expression : x(t) = −0,58 ×t2 + 0,65 × t.
 La fonction x est dérivable sur l’ensemble des réels. On note x′ sa dérivée.
 3. Déterminer x′(t) pour tout réel t.
x'(t) = -0,58 *2t +0,65 = -1,16t+0,65.
 4. Calculer x′(0).
x'(0) = 0,65 m/s.
5. Nommer la grandeur physique à laquelle fait référence x′(0).
La vitesse initiale.
6. Déduire de la question 3 la valeur de l’accélération définie sur l’intervalle de temps [0 ; 0,50], le temps étant exprimé en secondes. Interpréter le signe dans la situation étudiée.
x"(t) = -1,16 m s-2. La voiture décelère.
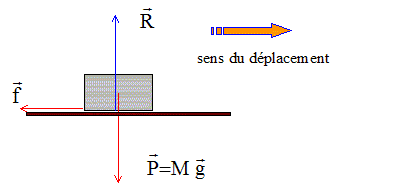
7. Réaliser le bilan des forces modélisant les actions mécaniques s’exerçant sur la voiture au cours de son mouvement. Les représenter sans souci d’échelle sur un schéma où la voiture est réduite à son centre de masse G.
Poids, verticale, vers le bas, valeur mg.
Action normale du plan, opposée au poids ;
Force de frottement, sens contraire du mouvement..

8. En utilisant la seconde loi de Newton, montrer que l’intensité f de l’ensemble des forces de frottement s’exerçant sur le système voiture s’écrit : f = −m x a.
Ecrire la seconde loi de Newton sur un axe horizontal orienté dans le sens du mouvement : f = -m a.
9. Montrer que la valeur numérique de l’intensité 𝐹 de l’ensemble des forces de frottements est égale à 4,6 × 10−2 N.
m = 0,040 kg ; a = -1,16 m s-2 ; f = 0,040 x1,16 =4,6 × 10−2 N.
On rappelle que la voiture parcourt une distance d avant de s’arrêter et que le travail de la force constante f entre le point de départ O et le point d’arrêt A s’écrit .
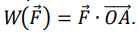
10. Montrer que W(f) = −f x d.
W = f x d x cos 180 = - f x d.
La variation de l'énergie cinétique du système voiture entre les instants t0 = 0 et tf = 0,5 s (instant à partir duquel on considère la vitesse nulle) est égale au travail de l’ensemble des forces de frottements.
11.En déduire la valeur de la distance d parcourue par la voiture entre les instants t0 et tf. Confronter le résultat obtenu à celui que l’on peut déterminer sur la figure 1.
Théorème de l'énergie cinétique : 0-½mv2= -f d.
d = ½mv2 / f =0,5 x 0,040 x0,652 / 0,046=0,18 m. En accord avec la figure.

Exercice 2. 5 points.
La mobilité décarbonée est un défi à relever afin de limiter la pollution engendrée par les modes de transport classiques. Une solution proposée est celle de véhicules électriques utilisant une pile à hydrogène qui nécessite du dihydrogène pour fonctionner. On s’intéresse à la production du dihydrogène par l’électrolyse de l’eau acidifiée par la présence d’acide sulfurique (2H +,SO4 2−) dans un électrolyseur de laboratoire de lycée. Lors de cette transformation chimique, l’eau se décompose et il se forme du dihydrogène et du dioxygène. Dans la littérature, les rendements indiqués dans le cas de l’électrolyse industrielle de l’eau sont compris entre 75 et 90 %. 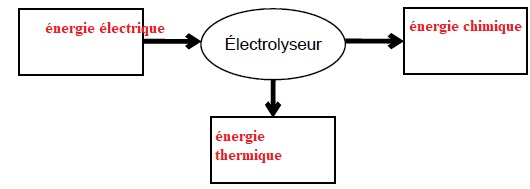Un électrolyseur est un dipôle qui convertit une partie de l’énergie électrique reçue en énergie chimique. Au laboratoire, on dispose de l’électrolyseur  dont la caractéristique tension-intensité est donnée ci-dessous.

Données : - Énergie chimique nécessaire à la formation d’un volume égal à 1,0 mL de dihydrogène, à la pression atmosphérique, lors de l’électrolyse de l’eau réalisée au laboratoire : 11 J.
- Couples oxydant/réducteur mis en jeu lors de l’électrolyse : H +(aq)/H2(g) et O2(g)/H2O(l).
1. Indiquer, en expliquant la réponse, si l’électrolyseur est un générateur ou un récepteur électrique. Schématiser la conversion énergétique qui a lieu dans l’électrolyseur en faisant apparaître les différentes formes d’énergie mises en jeu.
Un électrolyseur est un récepteur : il reçoit de l'énergie électrique qu'il convertit en énergie chimique et en énergie thermique.
 
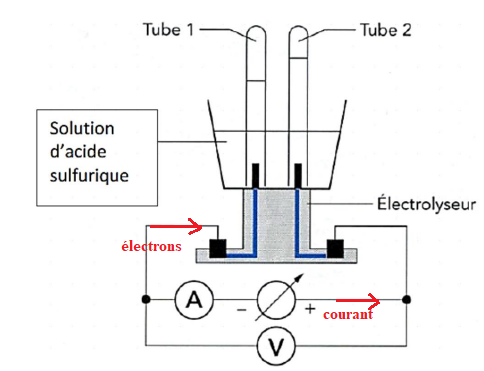
2. Compléter le schéma du montage d’électrolyse en indiquant le sens de circulation du courant et celui des électrons dans le circuit.

3. Écrire l’équation de la réaction modélisant la transformation se produisant au niveau de l’électrode reliée à la borne négative du générateur (à cette électrode, le dégagement gazeux se produit dans le tube 1).
 4. Préciser, en expliquant la réponse, si cette électrode constitue l’anode ou la cathode du dispositif.
Réduction à la cathode : 2H+aq + 2e- --> H2(g).
 5. Écrire l’équation de la réaction modélisant la transformation se déroulant lors de l’électrolyse de l’eau.
H2O(l) --> H2(g) + ½O2(g).
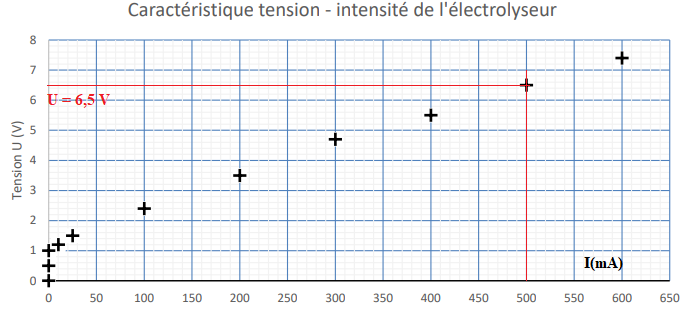
 6. Déterminer la valeur de la tension mesurée aux bornes de l’électrolyseur du laboratoire lorsqu’il est traversé par un courant électrique d’intensité égale à 500 mA.
U = 6,5 V.
 7. En déduire la valeur de la puissance électrique reçue par l’électrolyseur en fonctionnement dans ces conditions.
P = U I = 6,5 x0,5 = 3,25 ~3,3 W.
 On réalise au laboratoire l’électrolyse de l’eau pendant une durée de deux minutes avec une intensité du courant maintenue égale à 500 mA. Il se forme alors un volume de dihydrogène égal à 20 mL.
8. Montrer que la valeur de l’énergie électrique reçue par l’électrolyseur pendant les deux minutes de fonctionnement est environ égale à 400 J.
Energie E = U I t = P t = 3,25 x2 x60 =3,9 102 J.
 9. Déterminer le rendement de l’électrolyseur en fonctionnement. Commenter ce résultat par rapport à une électrolyse industrielle.
Données : - Énergie chimique nécessaire à la formation d’un volume égal à 1,0 mL de dihydrogène, à la pression atmosphérique, lors de l’électrolyse de l’eau réalisée au laboratoire : 11 J.
Energie chimique : 11 x20 = 220 J.
Rendement = énergie chimique / énergie électrique = 220 / 390 =0,56 ( 56 %), inférieure au rendement industriel.

...
....

 Mathématiques. 4 points.
Question 1 : Soit la fonction f définie sur [0; +∞[ par f(x) = (3x + 5)𝑒 x . Vérifier que f(0) est un nombre entier que l'on précisera.
f(0 = -5e0 =-5.
 Question 2 : Soit la fonction f définie et dérivable sur [0; +∞[ par f(x) = (x − 5)e3𝑥 . On note f ' sa fonction dérivée. Démontrer que pour tout x appartenant à l’intervalle [0; +∞[, f '(x) = (3x − 14)e3x .
On pose u = x-5; v = e3x ; u' = 1 ; v' = 3e3x.
u'v+v'u = e3x +3(x-5)e3x=(3x − 14)e3x .

Question 3 : On donne : 𝐴 = ln ( 25/ 8 ) En détaillant les calculs, écrire 𝐴 sous la forme aln(2) + bln(5), a et b étant deux nombres entiers relatifs.
A = ln(25) -ln(8) = ln(52) -ln(23) =2 ln(5) -3 ln(2).

Question 4 :  On considère l’équation différentielle (𝐸): 𝑦 ′ = 3𝑦 − 12, Où y est une fonction de variable x, définie et dérivable sur R. Déterminer la fonction f définie et dérivable sur R, solution de (E), qui vérifie f(0) = 8.
Solution générale de y' -3y=0 : y = Ae3x avec A une constante.
Solution particulière de (E) : y = 4.
Solution générale de (E) : y = Ae3x +4.
y(0) = A+4 = 8 ; A = 4.
y =4e3x+4.

Exercice 4. 6 points
L'acide benzoïque
L’acide benzoïque, de formule C6H5COOH, et le benzoate de sodium sont des conservateurs antimicrobiens respectivement identifiés par les codes E210 et E211. Ils sont présents dans de nombreux produits alimentaires et notamment dans certaines boissons gazeuses sucrées. À température ambiante, l’acide benzoïque est un solide blanc.
L’objectif de cet exercice est de vérifier l’indication d’une étiquette de boisson gazeuse concernant la présence d’un conservateur.
 1. Sur la formule topologique, entourer et nommer le groupe caractéristique présent.
 2. Écrire la formule topologique de l’ion benzoate, base conjuguée de l’acide benzoïque.

 3. Représenter le diagramme de prédominance du couple acide benzoïque/ion benzoate.

Dans un premier temps, on réalise deux expériences permettant de mettre en évidence les propriétés de l’acide benzoïque et de l’ion benzoate :
 • Expérience (1) : Dans un tube à essais contenant une solution de benzoate de sodium, on ajoute quelques gouttes d’acide chlorhydrique concentré. On observe qu’un solide blanc apparaît.
• Expérience (2) : Dans un tube à essais contenant une solution de soude concentrée, on ajoute de l’acide benzoïque solide. On observe que le solide introduit disparaît.
4. On donne l’équation chimique suivante : C6H5COO −(aq) + H3O +(aq) → C6H5COOH(aq) + H2O(l)
La réaction qui correspond à l’équation ci-dessus modélise une transformation chimique ayant lieu lors de l’une des expériences précédentes. Indiquer, en justifiant la réponse, s’il s’agit de l’expérience (1) ou de l’expérience (2).
Expérience 1 : les réactifs sont l'ion benzoate et l'ion oxonium présent dans l'acide chlorhydrique.
L’étiquette d’une boisson gazeuse indique qu’elle contient du benzoate de sodium comme conservateur alimentaire, entre autres, et on souhaite vérifier cette indication. On réalise pour cela une extraction liquide-liquide. On suit le protocole expérimental suivant :
 1. Verser 500 mL de boisson dans un grand bécher.
2. Ajouter de l’acide chlorhydrique jusqu’à amener le pH à environ 2.
3. Ajouter alors 40 mL d’éther éthylique, agiter et laisser reposer.
 4. Transvaser l’ensemble dans une ampoule à décanter.
5. Agiter vigoureusement pendant deux minutes en prenant soin de dégazer régulièrement pour éviter toute surpression.
 6. Laisser décanter.
7. Récupérer la phase aqueuse S dans un bécher et la phase organique dans un erlenmeyer.
5. Préciser ce qu’il se passe lors de l’étape 2 du protocole.
L'acide benzoïque peu soluble dans l'eau précipite.
6. À l’aide des données, expliquer pourquoi l’éther éthylique constitue un solvant extracteur plus adapté que l’éthanol lors de la réalisation de l’étape 3 du protocole.
L'éther éthylique est non miscible à l'eau contrairement à l'alcool éthylique.
7. Compléter le schéma , en justifiant, à l’aide des données, la nature et la position des différentes phases dans l’ampoule à décanter à l’issue de l’étape 6 du protocole.

8. Après évaporation du solvant extracteur, il reste une masse 𝑚 = 10,0 mg de solide blanc. Proposer une méthode expérimentale permettant de vérifier que ce solide blanc est bien de l’acide benzoïque.
Banc Kôfler, détermination du point de fusion.
9. Sachant que la concentration C en quantité de matière totale théorique d’ions benzoate dans cette boisson est égale à 4,0 × 10−4 mol L −1 , montrer que la masse théorique d’acide benzoïque que l’on devrait obtenir à l’issue de l’extraction est égale à 24 mg.
Soit 2,0 10-4 mol dans 500 mL.
M(acide benzoïque) =122 g / mol.
m = 2,0 10-4 x 122 =0,0244 ~0,024 g ou 24 mg.
10. Le rendement d’une extraction étant défini comme le rapport de la masse de substance réellement extraite sur la masse théorique de substance que l’on aurait pu extraire, calculer le rendement de cette extraction et l’exprimer en pourcentage. Commenter ce résultat.
Masse expérimentale / masse théorique = 10 / 24 =0,416 ( ~42 %). Ce rendement est assez faible.

  
menu