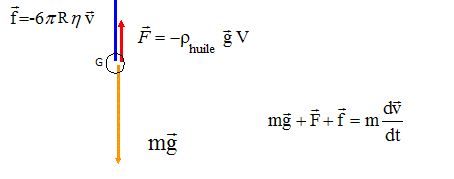Physique chimie et mathématiques, bac STI2D métropole 2023. Viscosimètre, ultrasons, conservation d'une boisson. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . .. . . . . .. .. ...... ... Le viscosimètre à chute de bille. 4 points  La viscosité d’une huile, notée h, est un paramètre exprimé en kg m-1 s -1 , dont la connaissance est essentielle pour toute utilisation de cette huile. Cet exercice propose un exemple de méthode de mesure de la valeur de la viscosité d’une huile de moteur Diesel du commerce. 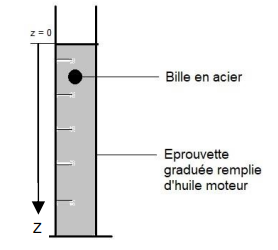Pour réaliser cette mesure, on utilise un « viscosimètre à chute de bille », constitué d’une éprouvette remplie d’huile de moteur dans laquelle est lâchée une bille métallique sphérique. On se place dans le référentiel terrestre supposé galiléen et la bille est lâchée sans vitesse initiale depuis la position z = 0. Les forces exercées sur la bille métallique sont : - Le poids P =mg avec m =20,1 g. - La poussée d’Archimède, notée Pa , de même direction que le poids P et de sens opposé. Sa valeur est Pa = rhuile V g, où rhuile =840 kg m-3 est la masse volumique de l’huile, V=5,6 10-6 m3 le volume de la bille. - La force de frottement fluide exercée par l’huile sur la bille est notée f . Elle est ici de même direction que le poids P et de sens opposé. Sa valeur est donnée par la relation f = 6 p h R v, où v est la valeur de la vitesse de la bille, h est la viscosité de l’huile et R =1,1 cm le rayon de la bille. Q1. Faire un schéma des forces s’appliquant sur la bille. Exprimer le poids de la bille en fonction de m et m puis calculer sa valeur. Calculer de même la valeur de la poussée d’Archimède Pa et justifier que la bille d’acier tombe dans l’huile quand on la lâche en 𝑧 = 0 avec une vitesse initiale nulle. Q2. En utilisant le principe fondamental de la dynamique, établir la relation liant le vecteur accélération , les forces s’exerçant sur la bille et la masse m de cette bille. 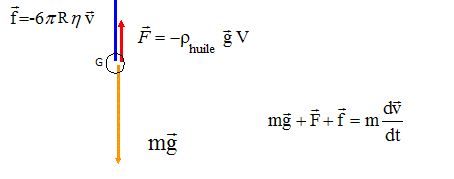P = mg = 20,1 10-3 x9,81 =0,197 N. Pa = 840 x5,6 10-6 x9,81 =0,046 N. Initialement la force de frottement fluide est nulle ; de plus P > Pa : la bille tombe.    Q3. On note v la fonction définie sur [0 ; +∞[ comme la projection du vecteur vitesse v sur l’axe (Oz). Montrer que v vérifie l’équation différentielle dv/dt = − 6phR / m v + g − rhuileV g / m . Sur l'axe Oz, la seconde loi de Newton s'écrit : m dv/dt = − 6phR v +m g − rhuileV g. Puis diviser par m. En explicitant les valeurs numériques, on admet que v est solution de l’équation différentielle (E) suivante où v(t) est exprimée en m·s-1 et t en s : (E) : dv / dt = −6,8 v + 7,5. Q4. Au début de l’expérience, la bille est introduite dans l’éprouvette avec une vitesse nulle. Démontrer que la solution v de cette équation sur [0 ; +∞[ vérifiant cette condition initiale est définie par : v(t) = − 75 / 68 exp( −6,8 t )+ 75 / 68 . Solution générale de dv /dt +6,8 v = 0 : v(t) = A exp(-6,8t) avec A une constante. Solution particulière de (E): v(t) =7,5 /6,8 = 75 / 68. Solution générale de (E) : v(t) =A exp(-6,8t) +75 / 68. v(t=0) = 0, d'où A = -75 /68. v(t) = − 75 / 68 exp( −6,8 t )+ 75 / 68 .  Q5. Déterminer la valeur exacte de la limite de v(t) en plus l'infini. En plus l'infini, le terme en exponentielle tend vers zéro. vlim =75 /68 m /s.  Q6. On mesure expérimentalement une vitesse limite vlim = 1,1 m /s . On peut en déduire la valeur de la viscosité h par la relation suivante : h = (m-rhuile V ) g / (6 pRvlim). Calculer cette valeur et comparer le résultat à la valeur h = 0,66 kg m-1 s -1 fournie par le fabricant. h =(20,1 10-3-840 x5,6 10-6) x9,81 / (6 x3,14 x0,011x1,1)=0,66 kg m-1 s -1 . Aide au stationnement. Les constructeurs automobiles proposent depuis plusieurs années des systèmes d’aide au stationnement ou de stationnement automatique qui reposent sur l’utilisation de capteurs à ultrasons. Quelques caractéristiques des ultrasons.  Q1. Parmi les propositions suivantes, indiquer sur votre copie celles qui sont exactes :  Affirmation A : les ondes ultrasonores sont des ondes électromagnétiques. Faux.  Affirmation B : les ondes ultrasonores sont des ondes mécaniques.  Vrai. Affirmation C : les ondes ultrasonores peuvent se propager dans le vide. Faux.  Affirmation D : les ondes ultrasonores nécessitent la présence d’un milieu matériel pour se propager. Vrai.  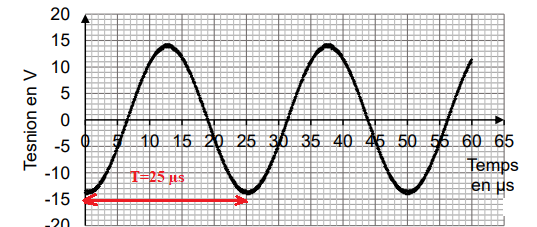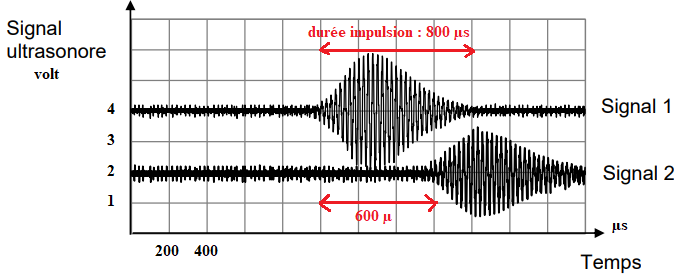Le document 1, représente la tension mesurée à l’oscilloscope par un détecteur recevant le signal émis par un émetteur d’ultrasons : Q2. Déterminer la fréquence f des ultrasons émis, en kHz et expliquer pourquoi le signal produit par l’émetteur n’est pas audible. Donnée : les ondes sonores audibles ont des fréquences comprises entre 20Hz et 20 kHz. f = 1 / T = 1 /(25 10-6) =40 000 Hz = 40 kHz > 2 kHz non audible pour l'homme. Utilisation des ultrasons pour déterminer une distance.  Le capteur à ultrasons utilisé dans le système d’aide au stationnement est un capteur « combiné » qui contient un émetteur et un récepteur d’ondes ultrasonores. La distance entre le capteur et l’obstacle est déduite de la durée qui s’écoule entre l’émission d’une impulsion ultrasonore et la réception de son écho par le capteur, connaissant la vitesse de propagation des ultrasons dans l’air. Une modélisation au laboratoire du capteur, à l’aide d’un émetteur et d’un récepteur à ultrasons indépendants, a permis d’obtenir la copie d’écran d’oscilloscope suivante dans le cas d’un obstacle situé à une distance de 10 cm. Q3. Indiquer, en donnant deux arguments, lequel des deux signaux (signal 1 ou signal 2) du document 3 est associé à l’onde réfléchie. L'onde réfléchie (signal 2) est en retard sur l'onde incidente ( signal 1). Q4. Le capteur combiné ne peut fonctionner correctement en récepteur que lorsqu’il a fini de fonctionner en émetteur. Préciser si la durée d’impulsion utilisée dans l’expérience permettrait de détecter correctement un obstacle situé à une distance de 10 cm. Durée impulsion : 800 µs. Durée pour parcourir 10 cm à la célérité v = 340 m /s : 0,1 / 340 =294 10-6 s = 294 µs < durée de l'limpulsion. La réception s'effectue alors que l'émission n'est pas terminée. Principe de fonctionnement d’un système de stationnement automatique. 6 points.  Certains systèmes embarqués effectuent automatiquement la manœuvre de stationnement du véhicule, sans intervention du conducteur. Cela n’est possible qu’après une phase de mesure qui permet de déterminer si la taille de la place est compatible avec la manœuvre. Dimensions minimales de la place de stationnement : longueur : 5,1 m ; largeur : 2,2 m. 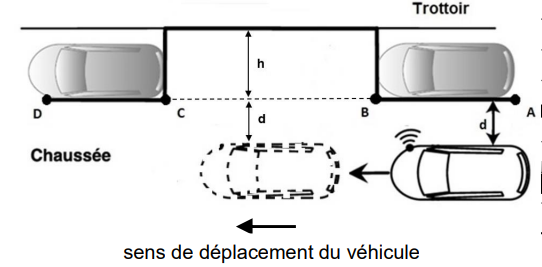Lors de la phase de mesure, la voiture est parallèle au trottoir et se déplace vers l’avant à vitesse constante le long de la place libre. 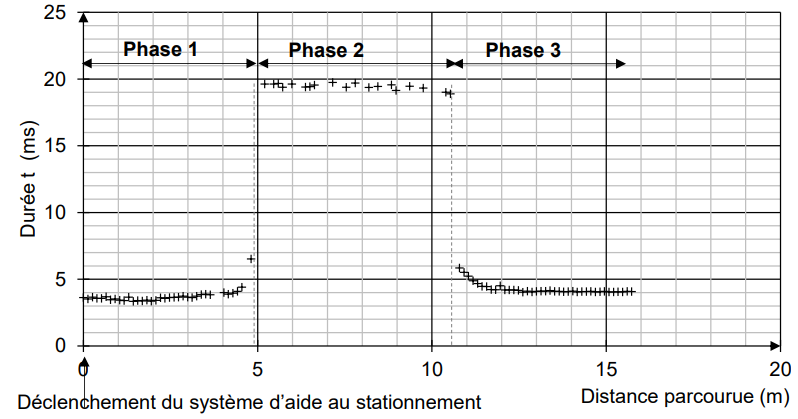On a réalisé un dispositif modélisant ce système grâce à un microcontrôleur et un émetteur-récepteur à ultrasons que l’on a fixé sur une voiture se déplaçant comme indiqué sur le document suivant : Q5. Durant la phase 2 du mouvement de l’automobile indiquée sur le document, le capteur à ultrasons se trouve au niveau de la place disponible (entre les points B et C ). Déterminer la durée de la phase 2 du mouvement de la voiture et en déduire la longueur de la place libre. Indiquer si celle-ci permet le stationnement de la voiture. Donnée : la voiture se déplace à la vitesse v0 = 1,3 m.s-1 . Distance parcourue durant la phase 2 : 5,05 m. Durée : 5,05 / 1,3 =3,88 s.  La distance d indiquée sur le document 5 désigne la distance latérale par rapport aux véhicules déjà stationnés. Q6. Sachant que la vitesse de propagation des ondes ultrasonores dans l’air est c = 340 m·s-1 montrer que la valeur de la distance d est comprise entre 0,6 m et 0,7 m. Calculer la profondeur h de la place libre et indiquer si celle-ci permet le stationnement de la voiture. Durée de la phase 1 : t1=4 ms. distance aller + distance retour des ultrasons : 2d = c t1=340 x4 10-3=1,36 m; d = 1,36 / 2 =0,68 m. Durée de la phase 2 : t2=16 ms. distance aller + distance retour des ultrasons : 2h = c t2=340 x16 10-3=5,44 m; h= 5,44 /2 =2,72 m. Cette profondeur est suffisante pour garer la voiture. ... .... Mathématiques. 4 points. Question 1 Pour cette question, indiquer la lettre de la réponse exacte. Aucune justification n’est demandée.  L’expression (e −3𝑥) 2×(e 2𝑥) −3 /(e 5𝑥×e 6𝑥) vaut : e-3x *e-3x / [(e 2𝑥) 3e5x+6x=e-6x/e17x = e-6x *e-17x =e-23x. Réponse D. Question 2 Soit f la fonction définie sur R par f(x) = e 2𝑥 (– 3𝑥 + 1). On admet que la fonction f est dérivable sur R et on note f 'sla fonction dérivée. Montrer que f '(x) = e 2𝑥 (−6𝑥 − 1). On pose u = e2x et v = 1-3x ; u' = 2e2x ; v' =-3 ; u'v+v'u=2(1-3x)e2x-3e2x=e2x(-1-6x). Question 3 On désigne par i le nombre complexe de module 1 et d’argument p/ 2 . Mettre le nombre complexe z=3½ + i sous forme exponentielle en détaillant les calculs. Module de z : |z| =( 3+1)½=2. z / |z| = 3½ / 2 +0,5i =cos (p/6) + i sin (p/6). z = 2 exp(ip/6). Question 4  Résoudre sur l’intervalle ]0 ; +∞[ l’équation : 2  ln(𝑥) /(3 ln(10))– 2,88 = 4. 2  ln(𝑥) /(3 ln(10))=6,88. ln(x) / ln(10) = 6,88 *3 /2=10,32. ln(x) =10,32 ln(10 )= ln(1010,32) ; x=1010,32~2,089 1010. Exercice 4. 6 points Les boissons en randonnée. Conservation d’une boisson chaude Dans la documentation fournie par un fabricant de bouteilles isothermes, on peut lire l’information suivante relative à un modèle donné : pour une température initiale de l’eau à 95 °C, la température vaut 82 °C au bout de 6 h et 73°C au bout de 12 h. On place 1,0 L d’eau à la température qi = 95 °C dans l’une de ces bouteilles isothermes. La température extérieure à la bouteille est q ext = 25 °C Q1. Exprimer la variation de l’énergie interne, DU, de l’eau contenue dans la bouteille isotherme, au cours des 6 premières heures en fonction de : la masse de l’eau, meau, la capacité thermique massique de l’eau, ceau, la température initiale de l’eau et la température de l’eau après 6h.. Montrer que DU est voisine de 54 kJ.  Données : - Capacité thermique massique de l’eau : ceau = 4,18 kJ·kg-1 ·°C-1 - Masse volumique de l’eau : reau = 1,0 kg L -1 ; - Température initiale qi = 95 °C ; - Température finale après 6 h qf = 82 °C ; - Volume de l’eau V = 1 L. DU = meau ceau (qf -qi)=1 x 4,18 x(82-95)= -54,34 ~ -54 kJ.  Q2. Définir le flux thermique à travers la paroi et montrer que le flux thermique moyen qui traverse la paroi de la bouteille au cours des 6 premières heures, Fmoyen, est voisin de 2,5 W. Fmoyen, = | DU| / Dt = 54,34 103 /(6 x3600)= 2,5 W. Au cours du refroidissement, le flux thermique entre l’eau et l’extérieur n’est pas constant. Il dépend de la différence de température Dq entre l’intérieur et l’extérieur de la bouteille et de la résistance thermique Rth de ses parois : F = Dq / Rth. Q3. Choisir sans calcul, parmi les trois propositions suivantes, la valeur du flux thermique à l’instant initial et justifier ce choix : a.  3,6 W;  b.  = 2,5 W ; c.  1,8 W . Le flux est proportionnel à la différence de température qui vaut 95-25 = 70°C au départ. Seule la proposition a convient. En déduire que la valeur de la résistance thermique Rth des parois de la bouteille isotherme est voisine de 19 K·W-1 . Rth = Dq / F = 70 / 3,6 =19,44 ~19 K·W-1 . Q4. Montrer que la paroi de la bouteille isotherme d’épaisseur e = 1,0 cm et de surface totale S = 0,098 m2 a une conductivité thermique l = 0,0052 W·m-1 ·K-1 . Donnée : La relation liant la résistance thermique d’une paroi plane 𝑅th, à sa surface S en m2 , à son épaisseur e en m, et à la conductivité thermique du matériau l en W·m-1 ·K-1 est la suivante : Rth = e / (lS). l = e / (Rth S) =0,010 / (19 x0,098)=5,4 10-3W·m-1 ·K-1 .  La documentation du fabricant indique que la bouteille est composée de 100 % d’acier inoxydable et qu’elle est munie de deux parois en inox séparées par un espace pratiquement vide. Q5. Expliquer, sans calcul, l’intérêt du vide partiel entre les deux parois de la bouteille. Le vide partiel diminue fortement le transfert thermique par conduction.  Approvisionnement en eau : les pastilles de purification.  Il existe des comprimés effervescents qui permettent de purifier l’eau. Le fabricant indique qu’il suffit d’ajouter un comprimé dans un litre d’eau non potable et d’attendre 30 minutes avant de la consommer. Un comprimé de masse 50 mg contient 3,5 mg de dichloroisocyanurate de sodium (noté NaDCC), de l’hydrogénocarbonate de sodium et de l’acide adipique. Q6. Déterminer la valeur de la quantité de matière n de NaDCC dans 1,0 L d’eau préparée en suivant les recommandations préconisées. Donnée : masse molaire du NaDCC : MNaDCC = 219,95 g·mol-1 . n = m / M = 3,5 10-3 / 219,95=1,6 10-5 mol. Lorsque le comprimé entre en contact avec l’eau, une transformation chimique a lieu, produisant de l’acide hypochloreux de formule HOCl dont la molécule contient un élément Chlore, Cl. Au cours de cette transformation chimique, une mole de NaDCC libère ainsi deux moles d’élément chlore. Q7. Calculer la masse d’élément chlore Cl qui se trouve dans 1,0 L d’eau à l’issue de son traitement à l’aide de la pastille effervescente. Donnée : masse molaire du chlore M(Cl) = 35,5 g·mol-1 . n(Cl )= 2 x1,6 10-5 =3,2 10-5 mol. Masse d'élément chlore : 3,2 10-5 x 35,5=1,1 10-3 g = 1,1 mg dans 1 L. Il est recommandé, en France, de maintenir une teneur de chlore libre aux alentours de 0,1 mg/L.. L’OMS recommande une valeur maximale de chlore libre dans l’eau potable de 5 mg/L. Q8. Préciser si l’eau purifiée avec un comprimé est potable. 0,1 < 1,1 < 5 mg/L : l'eau purifiée est potable.

menu