Imprimante
à jet d'encre continu. Bac Métropole 09 / 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
De nombreuses applications technologiques, dans des domaines très variés, reposent sur l’utilisation d’un champ électrique.
L’objectif de cet exercice est d’étudier le principe de fonctionnement
des imprimantes à jet d’encre continu dévié, principalement utilisées
pour imprimer les dates d’expiration figurant sur les produits
alimentaires.
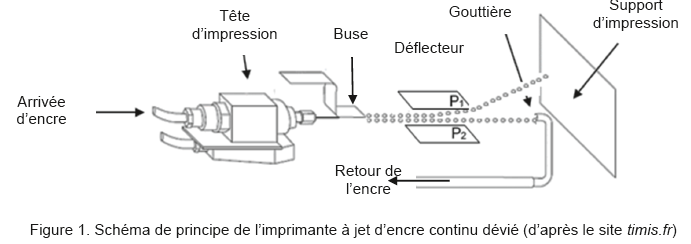
On donne sur le schéma de la figure 1, le principe de fonctionnement de
l’imprimante à jet d’encre continu dévié : le jet d’encre sort de la
tête d’impression par une buse qui le décompose en très petites gouttes
dont certaines sont chargées électriquement.
Celles-ci passent sous un déflecteur constitué de deux plaques P1 et P2 parallèles, chargées électriquement,
assimilables à un condensateur plan. Ces plaques dévient les gouttes chargées de leur trajectoire initiale.
Les gouttes non chargées poursuivent quant à elles leur mouvement
rectiligne vers une gouttière de recyclage et sont réintégrées dans le
module d’encre afin d’être réutilisées.
Données :
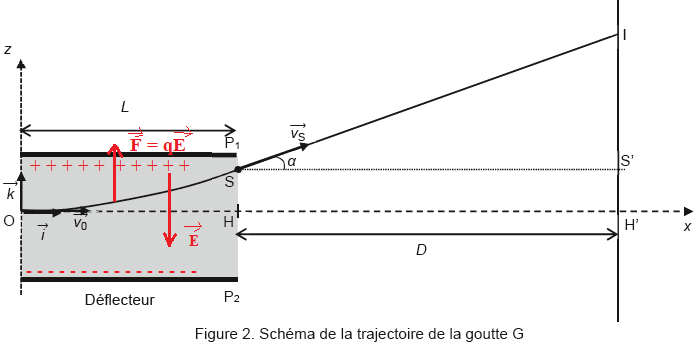
- les mouvements sont étudiés dans le référentiel terrestre supposé galiléen associé au repère représentés sur la figure 2.
- on considère que la charge électrique et la masse des gouttes d’encre
restent constantes entre la buse et le support d’impression ;
- masse d’une goutte d’encre : m = 2×10–10 kg ;
-charge électrique d’une goutte : q = – 4×10–13 C ;
- valeur de la vitesse d’éjection des gouttes d’encre : v0 = 20 m∙s–1 ;
- longueur des plaques du déflecteur : L = 2 cm ;
- distance entre le déflecteur et le support d’impression : D = 3 cm ;
- le champ électrique est supposé uniforme dans le déflecteur, E = 9×105 V∙m–1 ;
- le champ électrique est nul à l’extérieur du déflecteur ;
- hauteur moyenne d’un caractère imprimé : h = 3 mm ;
- intensité de la pesanteur : g = 9,81 m∙s-2.
On étudie le mouvement d’une goutte d’encre G, supposée ponctuelle, de masse m et de charge q négative.
À la date t0 = 0 s, la goutte d’encre G pénètre dans la zone
de champ électrique uniforme au niveau du point O avec une vitesse
initiale notée v0.
On suppose que l’action mécanique de l’air est négligeable devant les autres actions.
Q1. Indiquer les signes des charges portées par les plaques P1 et P2 sachant que la goutte chargée
négativement est déviée vers le haut.
On suppose que la valeur du poids de la goutte d’encre G est
négligeable par rapport à celle de la force électrique subie dans le
déflecteur.
Q2. Établir l’expression du vecteur accélération de la goutte d’encre en fonction de le masse m, de la
charge q et du vecteur champ électrique E.
Ecrire la seconde loi de Newton, la goutte n'étant soumise qu'à la force électrique.
Selon Ox : ax = 0 ; selon Oy : m az =qE ; ay = q / m E.
Q3. Montrer que les
équations horaires x(t) et y(t) du mouvement de la position de la
goutte d’encre G dans le déflecteur sont données par les relations :
La vitesse est une primitve de l'accélération :
vx = v0 ; vz =|q| / m E t.
La position est une primitive de la vitesse :
x(t) = v0 t ; z(t) = 0,5 |q| / m E t2.
Q4. Exprimer la date tS à laquelle la goutte d’encre G sort du déflecteur puis montrer que la valeur de la déviation HS est d'environ 0,9 mm.
L = v0 tS ; tS = L / v0 = 0,02 / 20 =1,0 10-3 s.
|HS| = 0,5 |q| / m E tS 2.
|HS| = 0,5 x4 10-13 / (2 10-10) x 9 105 x10-6 =9 10-4 m = 0,9 mm.
Q5. Exprimer les coordonnées du vecteur vitesse de la goutte d’encre G à la date tS.
vx = v0 =20 m /s ; vz =|q| / m E tS = 4 10-13 / (2 10-10) x 9 105 x10-3 =1,8 m /s.
Q6. Montrer que la valeur de l’angle a entre l’axe (Ox) et le vecteur vitesse vS est donnée par la relation :
tan α = |q|×E×L / (mv02).
tan α =vz / vx = |q| / m E tS / v0 = |q| / m E L / v02.
On suppose que le mouvement de la goutte entre le point S et le support d’impression est rectiligne uniforme.
Q7. En déduire la valeur de la hauteur H’I du point d’impact I de la goutte sur le support d’impression. Commenter.
tan α =S'I / D.
S'I = D tan α =D |q| / m E L / v02 =0,03 x4 10-13 x9 105 x0,02 /(2 10-10 x202) =2,7 10-3 m = 2,7 mm.
H'I =H'S' +S'I =0,9 +2,7 = 3,6 mm.
De l'ordre de grandeur de la taille des caractères des dates d'expiration.
Q8. Proposer, en justifiant, plusieurs moyens permettant d’augmenter la taille du caractère imprimé sur le support d’impression.
Augmenter D, E L, ou |q| ; diminuer m ou v0.
|