Mars
vue sous l'oeil de Kepler. Bac Métropole 09 / 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
On
étudie dans cet exercice la troisième loi de Kepler appliquée à la
planète Mars, puis on détermine les caractéristiques d’une lunette
astronomique permettant d’observer cette planète.
1. Étude et utilisation des lois de Kepler.
Donnée : valeur de l’unité astronomique (au, astronomical unit) : 1 au = 1,496×1011 m.
Le référentiel d’étude est le référentiel héliocentrique supposé galiléen : son origine est au centre du Soleil et
ses axes pointent vers des étoiles lointaines.
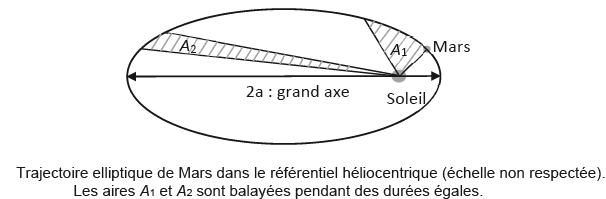
Q1. Énoncer les
deux premières lois de Kepler. En exploitant la deuxième loi et le
schéma, justifier que le mouvement de Mars dans le référentiel
héliocentrique n’est pas uniforme.
Première loi ou loi des orbites :
dans le référentiel lié au centre de la galaxie, l'orbite de chaque
étoile est une ellipse dont l'un des foyers est le centre de la galaxie.
Deuxième loi ou loi des aires : le mouvement de chaque planète est tel que le segment de droite reliant le soleil et la planète balaie des aires égales pendant des durées égales.
Les périodes de
révolution T (en année) et les demi-grands axes a (en unité
astronomique) des trajectoires des planètes du système solaire (à
l’exception de Mars) sont saisies dans un programme écrit en langage
Python, afin de vérifier la troisième loi de Kepler. Un extrait de ce
programme est donné.
Q2. Recopier sur la copie la ligne 8 du programme et la compléter.
Q3. Proposer sur la
copie un commentaire en précisant la finalité des lignes 16 et 17 du
programme et les unités des grandeurs calculées.

Q4. Commenter la figure 3 au regard des lois de Kepler.
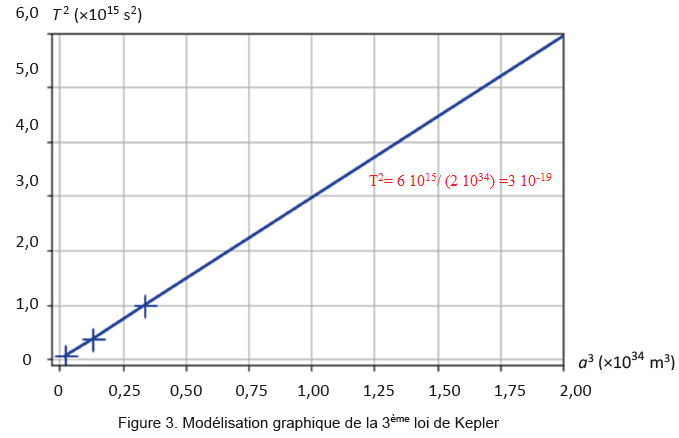
Le carré de la période de révolution est proportionnelle au cube du demi-grand axe de l'orbite.
À partir des relevés de Tycho Brahe, Kepler a pu déterminer que la période de révolution de Mars, notée TMars,
était de 687 jours.
Q5. Déterminer la valeur du demi-grand axe de l’orbite de Mars, noté aMars, et justifier qu’elle correspond à la quatrième planète du système solaire en partant du Soleil.
T2 / aMars3=3 10-19 ; aMars3=T2 / (3 10-19) =(687 *24 *3600)2 / (3 10-19) =1,17 1034.
aMars ~2,3 1011 m.

|
...
|
....
|
2. Observer Mars à l’aide d’une lunette astronomique.
Fondées
sur ce modèle, les lunettes astronomiques actuelles sont formées de
deux lentilles minces convergentes. On a représenté sur la figure
le schéma optique d’une lunette astronomique afocale.
Données :
- la distance minimale entre Mars et la Terre est de 62,07 millions de kilomètres ;
- à l’oeil nu, l’angle sous lequel est vue la Lune est de 9,0×10–3 rad ;
- le diamètre de Mars est de 6 794 km.
Q6. Sur la figure, on note L1 et L2
les deux lentilles minces convergentes. Préciser la lentille
correspondant à l’objectif et celle correspondant à l’oculaire de la
lunette.
L1 : objectif et L2 : oculaire.
On considère un objet situé à l’infini, noté A∞B∞. On observe cet objet avec la lunette.
Q7. Tracer sur la figure la marche des rayons lumineux provenant de B∞ à travers la lentille L1 et la lentille L2 en faisant apparaitre l’image intermédiaire, notée A1B1, de l’objet A∞B∞ à travers la lentille L1.
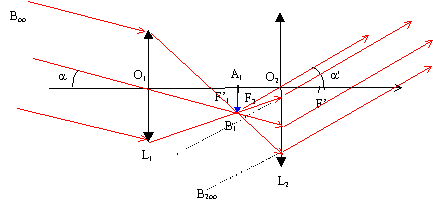
Q8. Représenter les angles a (angle sous lequel est vu Mars à l’oeil nu) et a' (angle sous lequel est vu Mars à l’aide de la lunette) sur la figure.
Q9.
Une lunette astronomique est caractérisée par son grossissement d’expression :
G = a' / a.
avec a l’angle sous lequel l’objet AB est vu à l’oeil nu et a’ l’angle sous lequel l’image A2B2 est vue à travers la lunette astronomique afocale.
En considérant les angles a et α' exprimés en radians comme petits, montrer que le grossissement de la
lunette astronomique afocale peut s’exprimer par la relation :
G =f1' / f2'.
Triangle O2F'1B1 : tan a' = A1B1/O2F2 ~ a' .
L'angle étant petit , on confond la tangente avec l'angle en radian.
Triangle O1F'1B1 : tan a = A1B1/O1F1 ~ a .
Grossissement G = a' / a =O1F1 /O2F2 =f '1 / f '2.
Q10. Dans la situation où Mars est au plus près de la Terre, déterminer parmi les oculaires fournis avec la lunette , celui qui permet à un observateur de voir Mars au moins aussi grosse que la Lune vue à l’oeil nu.
- à l’oeil nu, l’angle sous lequel est vue la Lune est de 9,0×10–3 rad ;
- le diamètre de Mars est de 6 794 km.
- la distance minimale entre Mars et la Terre est de 62,07 millions de kilomètres ;
a =6794 / ( 62,07 106)=1,09 10-4 rad.
a' =9,0×10–3 rad.
G = a' / a = 9,0 10-3 / (1,04 10-4) ~87.
f1' / f2'~87 ;
f '1 = 900 mm ; f '2 =900 / 87 ~10 mm.
|
|