Mathématiques, géométrie. Bac Métropole 09 / 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... L'espace est rapporté à un repère orthonormé. On considère les points A(1 ; 0 ; -1) ; B (3 ; -1 ; 2) ; C (2 ; -2 ; -1) ; D (4 ; -1 ; -2). On note D la droite de représentation paramétrique : x = 0 ; y =2+t ; z = -1+t avec t réel. 1.a. Montrer que les points A, B, C définissent un plan noté P. 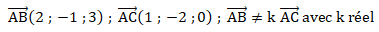Ces deux vecteurs n'étant pas colinéaires, les points A, B, C ne sont pas alignés ; ils définissent donc un plan. b. Montrer que la droite (CD) est orthogonale au plan P. Sur le plan P, que représente le point C par rapport à D ? Les droites (CD) et (AC) sont perpendiculaires en C. Donc C est le projeté orthogonal de D sur le plan P. c. Montrer qu'une équation cartésienne du plan P est  : 2x +y -z -3 = 0. Le vecteur CD( 2 ; 1 ; -1) est orthogonal au plan P ; une équation cartésienne du plan P est donc 2x +y -z +d = 0. C( 2 ; -2 , -1) appartient au plan P : 2*2-2-(-1) +d = 0 ; d =-3. Equation cartésienne du plan P   : 2x +y -z -3 = 0. 2.a. Calculer la distance CD. CD2 =(4-2)2 + (-1 -(-2))2 +(-2-(-1))2 =4+1+1=6 ; CD = 6½. b. Existe-t-il un point M du plan P différent de C vérifiant MD = 6½ ? Justifier. C est le projeté orthogonal de D sur le plan P. C est le point qui est à la plus courte distance du point D au plan P. Il n'existe donc pas d'autre point de P situé à cette distance 6½. 3.a. Montrer que la droite D est incluse dans le plan P. Soit M(x, y , z) un point commun à D et à P. Ces coordonéées vérifient le système : x = 0 ; y = 2+t ; z = -1+t avec t réel. 2x+y-z-3=0. 0+2+t-(-1+t)-3 = 0 ; 0 = 0. Cela signifie que D est incluse dans le plan P. Soit H le projeté orthogonal du point D sur la droite D. b. Montrer que H est le point de D associé à la valeur t = -2 dans la représentation paramétrique. Coordonnées d'un vecteur directeur de la droite D : n ( 0 ; 1 ; 1). De plus H( 0 ; 2+t ; -1+t). Coordonnées du vecteur DH : ( 4 ; 3+t ; 1+t). 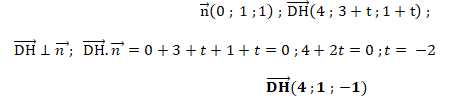c. En déduire la distance du point D à la droite D. DH2 = 42 +12 +(-1)2 =18 ; DH = 3 * 2½. ... .... L'espace est rapporté à un repère orthonormé. On considère les points : A ( -1 ; -2 ; 3) ; B (1 ; -2 ; 7) ; C ( 1 ; 0 ; 2). La droite D de représentation paramétrique : x = 1-t ; y = 2 ; z = -4 +3t avec t réel. Le plan P d'équation cartésienne : 3 x +2y +z-4 =0. Le plan Q d'équation cartésienne  : -6x-4y-2z+7 = 0. 1. Lequel des points suivants appartient au plan P ? R(1 ; -3 ; 1) ; S (1 ; 2 ; -1) ; T(1 ; 0 ; 1) ; U(2 ; -1 ; 1). 3 xR + 2yR +zR -4 = 3-6+1-4= -6 différe de zéro ; R n'appartient pas au plan P. 3 xS + 2yS +zS -4 = 3+4-1-4= 2 différe de zéro ; S n'appartient pas au plan P. 3 xT + 2yT +zT -4 = 3+0+1+1-4= 0 ; T appartient au plan P. 2. Le triangle ABC est : équilatéral ; rectangle isocèle ; isocèle non rectangle ; rectangle non isocèle. Le triangle ABC est rectangle en A. AB2 =22+02+42= 20 ; AC2 =22+22+(-1)2= 9 ; AB diffère de AC : le triangle ABC n'est pas isocèle. 3. La droite D est : orthogonale au plan P ; sécante au plan P ; incluse dans le plan P ; strictement parallèle au plan P. La droite D est donc parallèle au plan P. Le point H de coordonnées (1 ; 2 ; -4 ) appartient à la droite D. 3 xH + 2yH +zH -4 = 3+4-4-4= -1 différe de zéro ; H n'appartient pas au plan P. La droite D n'est donc pas incluse dans le plan P. 4. On donne le produit scalaire suivant :. Une mesure au degré près de l'angle ABC est : 34° ; 120° ; 90° ; 0°. Le triangle ABC étant rectancle en A, l'angle ABC est aigu. 5. L'intersection des plan P et Q est : un plan ; l'ensemble vide ; une droite ; réduite à un point. Donc les plans P et Q sont parallèles. 3 xT + 2yT +zT -4 = 3+0+1+1-4= 0 ; T appartient au plan P. -6 xT -4yT -2zT+7 = -6+0-2+7= -1 diffère de zéro ; T n'appartient pas au plan Q. Les plans P et Q sont strictement parallèles ; leur intersection est l'ensemble vide.

menu