Géométrie, Mathématiques, bac général Métropole 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Sujet 1. On considère le cube ABCDEFGH d’arête 1. On appelle I le point d’intersection du plan (GBD) avec la droite (EC). 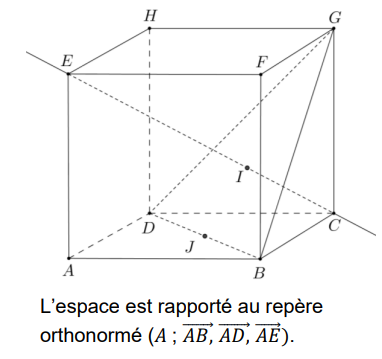1. Donner dans ce repère les coordonnées des points E, C, G. E (0 ; 0 ; 1) ; C(1 ; 1 ; 0) ; G (1 ; 1 ; 1). 2. Déterminer une représentation paramétrique de la droite (EC). Coordonnées du vecteur EC : 1 ; 1 ; -1. Représentation paramétrique de la droite (EC). x = t +xE = t  ; y = t+yE = t ; z = -t +zE = -t+1. 3. Démontrer que la droite (EC) est orthogonale au plan (GBD). 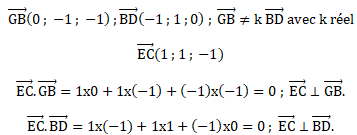 4. a. Justifier qu’une équation cartésienne du plan (GBD) est : x + y − z − 1 = 0. La droite (EC) est orthogonale au plan (GBD) : x +y -z +d = 0. B appartient à ce plan : 1+0-0+d=0 ; d = -1.  b. Montrer que le point I a pour coordonnées ( 2 /3 ; 2 /3 ; 1 /3 ). I appartient au plan (GBD) : xI + yI − zI − 1 = 0. I appartient à la drite (EC) ; t+t+t-1-1=0 ; t = 2/3. xI = 2/3 ; yI = 2/3 ; zI = 1-2/3=1/3. c. En déduire que la distance du point E au plan (GBD) est égale à 2x3½ / 3. EI = [(2/3-0)2 +(2/3-0)2 +(1/3 -1)2 ]½ =(12 /9)½=2x3½ / 3. . 5. a. Démontrer que le triangle BDG est équilatéral. BD, DG, BG représentent les diagonales des faces du cube ; elle sont égale à 2½. le triangle BDG est équilatéral.  b. Calculer l’aire du triangle BDG. On pourra utiliser le point J, milieu du segment [BD]. xJ = (xB+xD) / 2=0,5 ; yJ = (yB+yD) / 2=0,5 ; zJ = (zB+zD) / 2=0.  GJ=[(0,5-1)2 +(0,5-1)2 +(0 -1)2 ]½ =(3 / 2)½. Aire du triangle BDG : GJ x BD / 2 = (3 / 2)½ x 2½ / 2 =3½ /2.  6. Justifier que le volume du tétraèdre EGBD est égal à 1 / 3 . Aire du triangle BDG x hauteur EI / 3. 3½ / 2 x 2x3½ / 9= 1 /3. ... .... Sujet 2. Dans l’espace rapporté à un repère orthonormé, on considère : - le plan P1 dont une équation cartésienne est 2x + y − z + 2 = 0,  - le plan P2 passant par le point B(1 ; 1 ; 2) et dont un vecteur normal est n2(1 ; -1 ; 1). 1. a. Donner les coordonnées d’un vecteur n1 normal au plan P1. Vecteur n1(2 ; 1 ; -1) b. On rappelle que deux plans sont perpendiculaires si un vecteur normal à l’un des plans est orthogonal à un vecteur normal à l’autre plan. Montrer que les plans P1 et P2 sont perpendiculaires. 2. a. Déterminer une équation cartésienne du plan P2. x-y+z+d=0. B(1 ; 1 ; 2) appartient à ce plan : 1-1+2+d=0 ; d = -2. x-y+z-2=0.  b. On note D la droite dont une représentation paramétrique est : x=0 ; y = -2+t ; z =t avec t réel. Montrer que la droite D est l’intersection des plans P1 et P2. 2*0+(-2+t) -t +2=0 est vérifié, donc la droite D appartient au plans P1. 0-(-2+t)+t-2 = 0 est vérifié, donc la droite D appartient au plans P2.  On considère le point A(1 ; 1 ; 1) et on admet que le point A n’appartient ni à P1 ni à P2. On note H le projeté orthogonal du point A sur la droite D. 3. On rappelle que, d’après la question 2.b, la droite D est l’ensemble des points Mt de coordonnées (0 ; −2 + t ;t), où t désigne un nombre réel quelconque. a. Montrer que, pour tout réel t, AMt=(2t2-8t+11)½. AMt=[(0-1)2+(-2+t-1)2+(t-1)2]½=[1+9-6t+t2+t2-2t+1]½=(2t2-8t+11)½.  b. En déduire que AH = 3½. AH est la distance minimale de A à la droite D. 2t2-8t+11 =0 ; trinôme du second degré avec a =2 >0. Le minimum se situe à t = -(-8) / (2x2) =2 et vaut  : (2x22 -8x2 +11)½=3½. 4. On note D1 la droite orthogonale au plan P1 passant par le point A et H1 le projeté orthogonal du point A sur le plan P1. a. Déterminer une représentation paramétrique de la droite D1. Le vecteur de coordonnées n1(2 ; 1 ; -1) est un vecteur directeur de D1. Représentation paramétrique de la droite D1 : x =2t+xA =2t+1. y =t+yA=t+1. z = -t+zA = -t+1. b. En déduire que le point H1 a pour coordonnées (-1/3 ; 1 /3 ; 5 /3). H1 appartient au plan P1 d'équation cartésienne 2x + y − z + 2 = 0. 2(2t+1) +t+1 -(-t+1)+2=0 soit t = -2 /3. H1( -1/3 ; 1 /3 ; 5 /3). 5. Soit H2 le projeté orthogonal de A sur le plan P2. On admet que H2! a pour coordonnées (4 /3 ; 2 /3 ; 4 /3) et que H a pour coordonnées (0 ; 0 ; 2). Sur le schéma ci-dessous, les plans P1 et P2 sont représentés, ainsi que les points A, H1, H2, H. Montrer que AH1HH est un rectangle. De plus (AH) est orthogonale au plan P1, donc orthogonale à toutes les droites de ce plan, comme (H1H). Le parallélogramme AH1HH est un rectangle.

menu