Probabilités,
Mathématiques,
bac général Métropole
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Sujet 1.
Un technicien contrôle les machines équipant une grande entreprise.
Toutes ces
machines sont identiques.
On sait que :
- 20% des machines sont sous garantie ;
- 0,2% des machines sont à la fois défectueuses et sous garantie ;
- 8,2% des machines sont défectueuses.
Le technicien teste une machine au hasard.
On considère les événements suivants :
- G : « la machine est sous garantie » ;
- D : « la machine est défectueuse » ;
Pour répondre aux questions 1 à 3, on pourra s’aider de l’arbre
proposé ci-dessous.
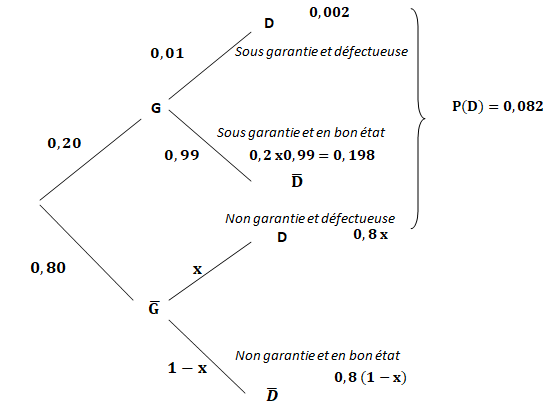 1.
1. La probabilité p G(D)
de l’événement D sachant que G est réalisé est égale à :
a. 0,002 ; b. 0,01vrai
; c. 0,024 ; d. 0,2.
pG(D)=p(G
n D) / p(G)=0,002 / 0,2=0,01.
2. La probabilité
p(non G ∩ D) est égale à :
a. 0,01 ; b. 0,08
vrai ; c. 0,1 ; d. 0,21
p(D) = 0,8x +0,002=0,082 ; 0,8x = 0,08.
3. La machine est
défectueuse. La probabilité qu’elle soit sous garantie est
environ égale, à 10 −3 près, à :
a. 0,01 ; b. 0,024
vrai ; c. 0,082 ; d. 0,1
p D(G)=p(G
n D) / p(D)=0,002 / 0,082 ~0,024.
Pour les questions 4 et 5, on choisit au hasard et de façon
indépendante n machines
de l’entreprise, où n désigne un entier naturel non nul. On assimile ce
choix à un tirage
avec remise, et on désigne par X la variable aléatoire qui associe à
chaque lot de n
machines le nombre de machines défectueuses dans ce lot.
On admet que X suit la loi binomiale de paramètres n et p = 0,082.
4. Dans cette
question, on prend n = 50.
La valeur de la probabilité p(X > 2), arrondie au millième, est de :
a. 0,136 ; b. 0,789
vrai ; c. 0,864 ; d. 0,924.
p(X > 2) =1 -p(X <2)=1-0,2114~0,789.
5. On considère un entier
n pour lequel la probabilité que toutes les machines
d’un lot de taille n fonctionnent correctement est supérieure à 0,4. La
plus
grande valeur possible pour n est égale à :
a. 5 ; b. 6 ; c. 10 vrai
; d. 11.
p(X=0)=( 10 0) x0,082 0 x-1-0,082) n
= 0,918 n.
0,918n
> 0,4 ; n ln(0,0918) > ln(0,4) ; n < ln(0,4) / ln(0,918)
; ln(0,4) / ln(0,918) ~ 10,7 ; n < 10.
|
...
|
....
|
Sujet 2.
Un jeu vidéo possède une vaste communauté de joueurs en ligne. Avant de débuter une partie,
le joueur doit choisir entre deux « mondes » : soit le monde A, soit le monde B.
On choisit au hasard un individu dans la communauté des joueurs.
Lorsqu’il joue une partie, on admet que :
-la probabilité que le joueur choisisse le monde A est égale à 2 /5 ;
- si le joueur choisit le monde A, la probabilité qu’il gagne la partie est de 7 / 10 ;
- la probabilité que le joueur gagne la partie est de 12 / 25 .
On considère les évènements suivants : A « Le joueur choisit le monde A » ;
B : « Le joueur choisit le monde B » ;
G : « Le joueur gagne la partie ».
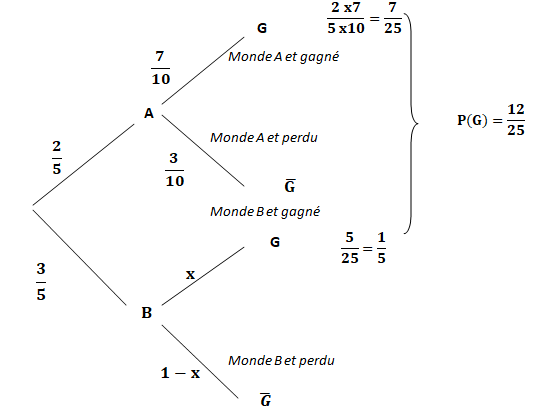
1. La probabilité que le joueur choisisse le monde A et gagne la partie est égale à :
a. 1 /5 ;
b. 3 / 25 ; c. 7 / 25 vrai ;
d. 24 / 125.
p(A n G)=2 / 5 x 7 / 10 =14 / 50= 7 /25.
2. La probabilité PB(G) de l’événement G sachant que B est réalisé est égale à :
a. 1 /5 ;
b. 1 /3 ;
c. 7 /25 ;
d. 5 / 12.
PB(G)=P(B n G) / P(B)=1 / 5 / (3 / 5) = 1 /3.
Dans la suite de l’exercice, un joueur effectue 10 parties successives. On assimile cette
situation à un tirage aléatoire avec remise. On rappelle que la probabilité de gagner une partie
est de 12 / 25.
3. La probabilité, arrondie au millième, que le joueur gagne exactement 6 parties est égale à:
a. 0,859 ; b. 0,671; c. 0,188 vrai; d. 0,187.
Gagner ou perdre une partie est un schéma de Bernoulli de paramètre p = 12 / 25.
On répète 10 fois cette expérience de manière identique et
indépendante. La variable aléatoire X suit la loi binomiale de
paramètres
n = 10 et p = 12 / 25.
p(X=6)=(10 6) x(12 /25)6 x(13 / 25)4 ~0,188.
4. On considère un entier naturel n pour lequel la probabilité, arrondie au millième, que le
joueur gagne au plus n parties est de 0,207. Alors :
a. n = 2; b. n = 3 vrai; c. n = 4; d. n = 5.
On cherche p(X < n)~0,188.
La calculatrice conduit à n = 3.
5. La probabilité que le joueur gagne au moins une partie est égale à :
a. 1 − (12 / 25)10;
b. (13 / 25)10
; c. (12 / 25)10
; d. 1 − (13 / 25)10 vrai.
p(X>1)=1-P(X=0)=1-(10 0) x(12 /25)0 x(13 / 25)10 =1-(13 /25)10.
|
|