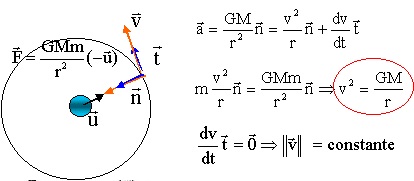Comprendre
les nuages,
bac général Centre étrangers
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Pourquoi les nuages ne tombent-ils pas
Pour mieux comprendre ce qui permet au nuage de rester en suspension, on s’intéresse à une
gouttelette d’eau présente dans ce nuage. On modélise la situation de la gouttelette de la façon
suivante :
- la gouttelette est supposée sphérique de rayon r = 1,0 10-5m ;
- la gouttelette n’est soumise qu’à son poids P et à une force verticale F exercée par l’air,
dirigée vers le haut ;
- la gouttelette est supposée initialement immobile dans le référentiel terrestre supposé
galiléen ;
la valeur de la force exercée par l’air sur la gouttelette s’exprime de la façon suivante :
F = k · h · r · v ;
k : coefficient sans unité ; k = 18,8 ; h : viscosité de l’air ; h = 15×10-6 kg·m-1·s-1
r : rayon de la goutte (en m)
v : vitesse de l’air dans un référentiel lié à la
gouttelette (en m·s-1)
Q.1. Montrer que la valeur P du poids de la goutte est environ 4,1×10-11 N.
Volume de la goutte : V = 4 / 3 x 3,14 x (1,0 10-5)3 =4,19 10-15 m3.
Masse : m= 4,19 10-15 x1000 = 4,19 10-12 kg.
Poids P = m g = 4,19 10-12 x9,81 =4,1×10-11 N.
Q.2. Déterminer la valeur F de la force verticale ascendante exercée par l’air sur la gouttelette
pour une vitesse verticale de l’air de 0,10 m·s-1
.
F = 18,8 x 15 10-6 x1,0 10-5 x0,10 =2,8 10-10 N.
Q.3. En déduire si la goutte monte, tombe ou reste immobile. Justifier.
F > P, la goutte monte.
Différents phénomènes (notamment des collisions) peuvent amener le rayon des gouttelettes à
augmenter, provoquant leur chute, sous forme de pluie.
On suppose que la vitesse verticale ascendante de l’air reste inchangée.
Q.4. En exploitant les réponses aux questions précédentes, déterminer le rayon minimum que
doit posséder une gouttelette pour tomber.
A la limite de la chute P = F.
P = 4 /3 x3,14 r3 x 1000 x9,81 =4,11 104 r3.
F = 18,8 x 15 10-6 r x 0,10 =2,82 10-5 r.
4,1 104 r3 = 2,82 10-5 r.
r2 =6,88 10-10 ; r =2,6 10-5 m = 26 µm.
B. Earthcare, un satellite pour étudier les nuages
Le satellite effectuera
environ 16 fois le tour de la Terre chaque jour.
masse de la Terre : M = 5,97×1024 kg ;
- rayon de la Terre : R = 6,37×103
km ;
- on considère que le satellite EarthCARE (noté S, de masse m) supposé ponctuel est en
mouvement circulaire autour de la Terre à une altitude h = 390 km.
Q.5. Exprimer la force d’interaction gravitationnelle que la Terre exerce sur le satellite.
Q.6. En appliquant la seconde loi de Newton et en utilisant le repère de Frenet, montrer que le
mouvement du satellite est uniforme.
Q.7. Montrer que la valeur de la vitesse v du satellite est donnée par la relation :
v =
G × (MT
/r )½ avec r = R+h.
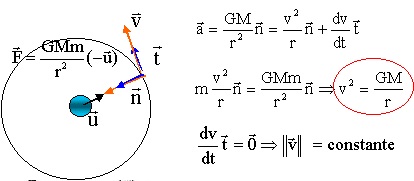
La norme de la vitesse étant constante, le mouvement est uniforme.
Q.8. Déduire des questions précédentes que la période de révolution du satellite est donnée par
la relation :
T = 2p (r3 / (GM))½.
Le satellite décrit la circonférence 2 p r à la vitesse v pendant la durée T.
2 p r= v T ; T =2 p r / v.
v =(GM / r)½ ;
T =2 p (r3 / (GM))½.
9. Calculer la valeur de la période de révolution T et déterminer si cette valeur est en accord
avec la phrase d’introduction : « Le satellite effectuera environ 16 fois le tour de la Terre
chaque jour. »
r=6,37×103 +390 =6,76 103 km = 6,76 106 m.
T = 2 x3,14 x[(6,76 106)3 / (6,67 10-11 x5,97 1024)]½ =5,53 103 s ou1,54 heures.
24 / 16 = 1,5 heures.
Ces valeurs sont en accord.
|
...
|
....
|
C. Radar profileur de nuage
Le satellite Earthcare, en passant au-dessus d’un nuage, pourra faire des analyses de ce nuage
grâce à des instruments embarqués. L’un de ces instruments est un radar profileur de nuage,
nommé Cloud Profiling Radar (CPR) dont le rôle est notamment d’étudier les mouvements verticaux
des gouttelettes dans le nuage.
Le radar CPR envoie vers le nuage des ondes électromagnétiques. Les gouttelettes (dont le
diamètre est de l’ordre de 10 à 100 µm) présentes dans le nuage renvoient une partie de ces ondes
vers le satellite. Le signal reçu par le satellite est analysé.
Pour obtenir un signal exploitable, la longueur d’onde des ondes électromagnétiques émises par le
CPR doit être supérieure à dix fois celle du diamètre des gouttelettes.
D’après Wikipédia.
Le CPR utilise des ondes électromagnétiques de fréquence fe = 94,05 × 109
Hz.
Q.10. Déterminer si les ondes électromagnétiques utilisées par le CPR permettent d’obtenir un
signal exploitable. Justifier la réponse.
le = c / fe =3,0 108 / (94,05 109) =3,2 10-3 m.
Pour être exploitable, la longueur d'onde des ondes doit être
supérieure à 10 fois le diamètre des plus grosses gouttes soit 10 x100
10-6 =10-3 m.
le > 10-3 m, donc le signal est exploitable.
Le satellite EarthCARE est situé à 390 km d’altitude à la verticale d’un nuage. Il se déplace à la
vitesse v = 7,5×103
m·s-1 par rapport au sol. Le nuage de dimension horizontale d’environ 1 km est
immobile par rapport au sol et situé à une altitude moyenne de 2 km.
Q.11. Vérifier que la distance parcourue par le satellite durant le temps d’un aller-retour des ondes
électromagnétiques entre le satellite et le nuage est très inférieure à la longueur du nuage.
On négligera l’épaisseur du nuage.
Durée d'un aller-retour des ondes entre nuage et satellite :
2 x(390-2) 103 / (3,0 108) =2,6 10-3 s.
Distance parcourue par le satellite : 7,5 103 x2,6 10-3=19,5 ~20 m << 1 km.
D. Une expérience contestée
En février 2021, divers journaux ont rapporté une expérience scientifique étonnante. Une équipe de
l’université chinoise de Qinghai vient de tester l’effet d’un son très puissant : sous l’influence des
ondes acoustiques émises à 160 dB, les précipitations auraient augmenté.
La mesure du niveau sonore de 160 dB a été réalisée à 1,0 m du haut-parleur.
Dans un article en ligne du journal anglais Dailymail du 5 février 2021, un journaliste relate avec
enthousiasme cette expérience et affirme que les ondes sonores utilisées sont à peine audibles.
Pendant l’expérience réalisée par l’université chinoise de Qinghai, une personne se place à une
distance d du haut-parleur.
Q.12. Estimer la distance d minimale pour qu’une personne ne subisse pas de gêne liée au bruit
du haut-parleur. Commenter le point de vue du journaliste.
Cas du haut-parleur : I = I0 x 100,1 L =10-12 x 1016 = 104 W m-2.
Puissance de la source sonore : P = 4 pr2 I =4 x3,14 x1,02 x104=1,26 105 W.
Absence de gène : L =50 dB.
I = I0 x 100,1 L =10-12 x 105 = 10-7 W m-2.
Distance de la source : d2 =P / (4 p I) =1,26 105 / (4 x3,14 x10-7)= 1,0 1011 ; d ~ 3 105 m ( environ 300 km).
L'affirmation du journaliste est fausse.
|
|