Correction de la trajectoire d'un nanosatellite, bac Centres étrangers 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Le nanosatellite Beihangkongshi-1 a été lancé par une fusée LongMarch le 6 novembre 2020 et placé en orbite autour de la Terre sur une trajectoire circulaire de rayon r.  Masse de la Terre : M = 5,9736×1024 kg ;  masse du satellite Beihangkongshi-1 : m = 20 kg.  Le référentiel d’étude est le référentiel géocentrique : son origine coïncide avec le centre de la Terre et ses axes pointent vers des étoiles lointaines. Il est supposé galiléen. 1. Recopier, sans souci d’échelle, la figure  en y faisant figurer le repère de Frenet et la force  modélisant l'action gravitationnelle exercée par la Terre sur le nanosatellite supposé ponctuel. 2. À l’aide de la deuxième loi de Newton donner l’expression du vecteur accélération du nanosatellite . 3. Établir que le mouvement est uniforme et que l’expression de la norme du vecteur vitesse est : v =(GM / r)½. 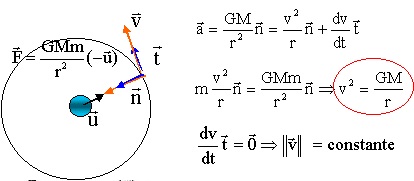La norme de lavitesse étant constante, le mouvement est uniforme. Dans les faits, on observe une diminution de l’altitude du nanosatellite au cours du temps. Pour pallier cette baisse d’altitude, un moteur présent sur le nanosatellite le replace régulièrement sur son orbite originale. Le suivi de la position du nanosatellite étudiée dans le référentiel géocentrique schématisé sur la figure 1 permet d’établir la courbe reproduite sur la figure 2 qui représente l’évolution de la valeur du rayon r de son orbite en fonction du temps, depuis sa mise en orbite jusqu’à la première correction de trajectoire le 31 décembre 2020 repérée par une flèche. 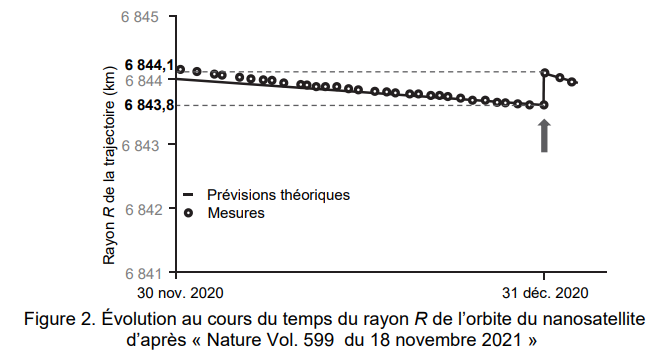4. À l’aide de la question 3 et de la figure 2, calculer la valeur v1 de la vitesse du nanosatellite le 30 novembre 2020 et la valeur v2 le 31 décembre 2020 avant la correction de trajectoire. Commenter l’évolution de la valeur de la vitesse du nanosatellite sur l’intervalle de temps considéré. v1 =  [6,6743 10-11 x 5,9736×1024  / ( 6844,1 103)]½ =7632,4 m /s. v2 =  [6,6743 10-11 x 5,9736×1024  / ( 6843,8 103)]½ =7632,6 m /s. La vitesse du satellite varie très peu sur la période considérée. La baisse d’altitude peut être expliquée par la présence d’une atmosphère résiduelle qui exerce une force de frottement sur le nanosatellite.  5. Rappeler l’évolution de la valeur de la vitesse d’un objet soumis uniquement à une force de frottement. En déduire qu’il y a contradiction apparente avec les résultats de la question 4. L'énergie mécanique diminue du travail des frottement. La vitesse diminue sous l'action de la force de frottement, contrairement au résultat de la question 4.  Dans la situation considérée, on admet que l’énergie potentielle du satellite a pour expression Ep = - G ·M·m /  r . 6. Rappeler la définition de l’énergie cinétique Ec, puis l’exprimer en fonction de G, M, m et r. Donner l’expression de l’énergie mécanique du satellite dans cette situation et montrer qu’elle peut s’écrire Em = - G ·M·m / ( 2r). Ec = ½mv2 ; v2 = GM / r ; Ec = ½GM m / r. Em = Ep + Ec = - G ·M·m /  r + ½GM m / r = - G ·M·m / ( 2r). ... .... Les représentations graphiques de l’énergie mécanique Em, de l’énergie potentielle Ep et de l’énergie cinétique Ec en fonction de r sont données sur la figure 3. Sur cette figure la courbe 2 représente l’énergie mécanique. 7. Attribuer en justifiant les énergies Ep et Ec aux deux courbes 1 et 3 de la figure 3. 8. À l’aide du graphique, indiquer comment évolue l’énergie mécanique Em lors de la diminution du rayon r de la trajectoire du nanosatellite. Montrer que cette évolution est cohérente avec la présence d’une force de frottement. L'énergie mécanique est négative : elle diminue si le rayon r diminue. L'énergie mécanique diminue du travail des frottements.

menu