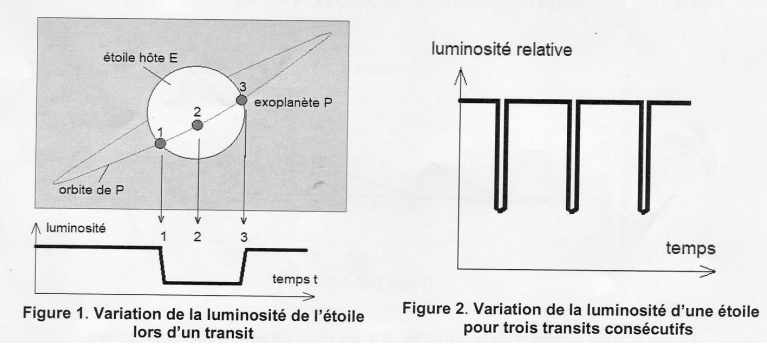
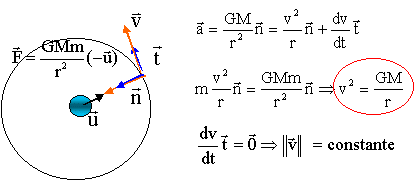L'exoplan�te, not�e P, orbite autour de son �toile, not� E.
A. D�tection par la m�thode du transit.
On mesure r�guli�rement la luminosit� d'une �toile afin de d�tecter la
baisse p�riodique de sa luminosit�, associ�e au passage par
rapport � l'observateur d'une exoplan�te devant l'�toile.
1. Justifier le terme p�riodique � partir de la figure suivante.
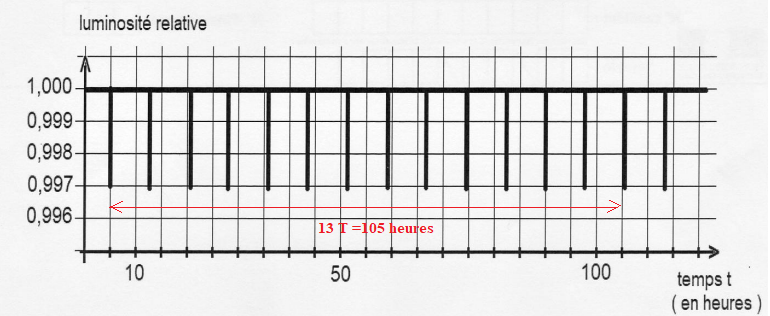
La courbe se reproduit indentique � elle m�me au bout d'un temps not� T.
2. D�terminer T.
T= 105 / 13 ~8,1 heures.
B. Mouvement de l'exoplan�te.
Dans le r�f�rentiel de l'�toile, on consid�re que l'orbite de P est circulaire, de centre O ( centre de l'�toile), de rayon r.
La masse de l'exoplan�te est not�e m et la masse de l'�toile est M = 9,5 1029 kg.
3. Repr�senter la force gravitationnelle exerc�e par E sur P.
4. Ecrire l'expression vectorielle de cette force.
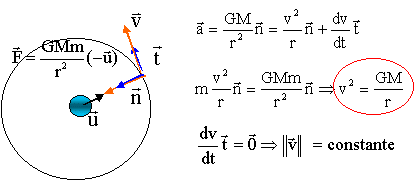
5. Enoncer la deuxi�me loi de Kepler ou loi des aires.
6. Compl�ter la figure afin d'illustrer cette loi et justifier que le mouvement de P est uniforme.
Le mouvement de chaque plan�te est tel que le segment de droite reliant l'�toile et la plan�te balaie des aires �gales pendant des dur�es �gales.
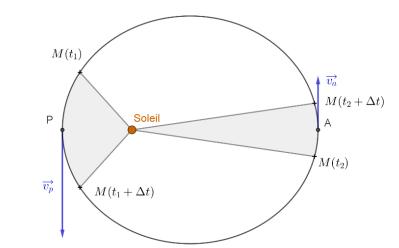
Les aires hachur�es sont �gales.
7. Appliquer la seconde loi de Newton � P et montrer que sa vitesse est v=(GM / r)�.
Voir sch�ma ci-dessus.
La seule force appliqu�e est la force gravitationnelle exerc�e par l'�toile.
Le vecteur acc�l�ration est dirig� vers le centre du soleil.
La
composante de l'acc�l�ration �tant nulle suivant le vecteur t de la
base de Frenet, la norme du vecteur vitesse ne change pas (mouvement
uniforme)
8.
Donner l'expression de sa p�riode de r�volution T en fonction de sa
vitesse v et du rayon de l'orbite r. En d�duire la troisi�me loi de
Kepler.
Dur�e (s) n�cessaire pour d�crire une circonf�rence ( 2pr en m�tre) � la vitesse v ( m/s).
2pr = v T ; T= 2pr / v.
Expression de T en fonction de G, M et r :
Elever au carr� l'expression de la p�riode : T2 = 4p2 r 2 / v2.
Remplacer v2 par son expression GM/ r : T2 = 4p2 r 3 / (GM).
9. On admet que T = 7,7 heures. Montrer que r est voisin de 1 million de km.
r3=GM T2 / (4p2)=6,67 10-11 x 9,5 1029 x(7,7 x3600)2 / (4 x3,142)=1,2 1027 m3.
r =1,07 109 m =1,07 106 km.
